鱼雷发动机参数自整定PID控制

路　骏，韩勇军，杨赪石，彭　博，万荣华，韩新波，马为峰

(中国船舶重工集团公司第七〇五研究所，陕西西安710075)

鱼雷发动机参数自整定PID控制

路骏，韩勇军，杨赪石，彭博，万荣华，韩新波，马为峰

(中国船舶重工集团公司第七〇五研究所，陕西西安710075)

摘要:提出一种用于鱼雷发动机的参数自整定PID控制方法。该方法利用支持向量机的非线性函数拟合能力辨识发动机的动态特性，采用粒子群算法实现PID控制器的参数优化。仿真实验表明，支持向量机能很好地拟合发动机的动态特性，基于粒子群算法的参数自整定PID控制器响应快速、无超调，控制效果良好，具有工程应用价值。

关键词:鱼雷发动机; PID控制;支持向量机;粒子群算法;参数优化

Self-tuning PID control scheme for torpedo engine

LU Jun，HAN Yong-jun，YANG Cheng-shi，PENG Bo，WAN Rong-hua，HAN Xin-bo，MA Wei-feng
(The 705 Research Institute of CSIC，Xi'an 710075，China)

Abstract:This paper presents a self－tuning PID control scheme for torpedo engine．Due to its excellent performance in nonlinear function approximation，support vector machine is used to identify the dynamics of torpedo engine．The PID parameters are tuned using particle swarm optimization．The simulation results demonstrate that the support vector machine is able to approximate engine dynamics with high accuracy，and the proposed controller achieves good performance in terms of convergence speed and overshoot．

Key words:torpedo engine; PID control; support vector machine (SVM) ; particle swarm optimization (PSO) ;parameter optimization

0　引言

PID控制具有算法简单、鲁棒性好、可靠性高等优点，因而被广泛应用于系统控制领域。PID参数整定是影响PID控制效果的关键问题［1］。目前工程上PID参数的整定方法主要有临界比例度法、衰减曲线法、Z－N法、快速整定法和继电器法等。这些方法在实际应用中虽然可以不同程度地满足要求，但由于PID控制器本身存在着静态和动态之间、跟踪设定值与抑制扰动之间、鲁棒性与控制性之间等矛盾，使得PID参数整定依然是一个重要的研究课题。

近年来，越来越多的人工智能方法被应用于PID控制器设计和参数整定中［2］。如出现了基于神经网络和遗传算法的PID控制器参数整定与优化方法［3－4］。但神经网络是基于经验风险最小原则，存在着神经网络结构和参数难以选择、易陷于局部极值、过拟合等问题。

支持向量机［5］(support vector machines，SVM)是基于统计学习理论发展起来的一种新的分类和回归工具，它通过结构风险最小化原理提高泛化能力，克服了神经网络的上述缺陷，已被成功应用于模式识别和系统控制领域［6］。粒子群算法［7］(particle swarm optimization，PSO)是基于群体智能理论的优化算法，通过种群中粒子间的合作与竞争产生的群体智能指导优化搜索，具有算法简单、收敛速度快、不容易陷入局部极值的优点，目前已广泛应用于函数优化和模糊系统控制等领域［8］。结合二者的优点，本文提出一种基于支持向量机和粒子群算法的参数自整定PID控制器，并将其应用于鱼雷发动机控制。仿真研究表明该方法具有满意的控制效果。

1　控制器设计

基于支持向量机的参数自整定PID控制策略如

图1所示。该控制策略利用作为发动机辨识模型的支持向量机产生预测信号，然后利用粒子群优化算法求解出最优PID参数，从而实现对发动机的预测控制。具体算法流程如下:

1)由控制要求获取未来的期望输出序列，即参考轨迹yr(k + 1) ;

2)预先测量得到发动机的开环输入输出数据，把它们作为训练支持向量机的样本，对支持向量机进行离线训练，得到具有足够精度的支持向量机模型;

3)利用支持向量机模型产生系统的预测输出yp(k + 1) ;

4)将预测输出与参考轨迹比较，计算未来时刻的期望误差e(k + 1)。

5)通过粒子群算法极小化性能指标函数J(k)，获得最优PID参数kp，ki，kd;

6)将控制量u(k + 1)作用于系统，返回1)。

图1　基于SVM的参数自整定PID控制器框图Fig.1 Scheme of self-tuning PID controller based on SVM

1.1支持向量机原理

用于系统辨识的支持向量机基本原理是:给定n组样本数据{ (yk，xk) | k = 1，…，n}，其中xkRn是输入样本，ykR是输出样本，利用一个非线性映射Ф将数据从原空间映射到高维特征空间F，并在此空间构造最优线性回归函数使其能够很好的逼近给定数组［4］。由统计学习理论可知，该函数具有以下形式

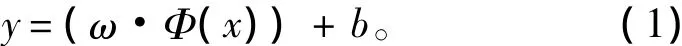
在Vapnik ε不敏感损失函数的定义下

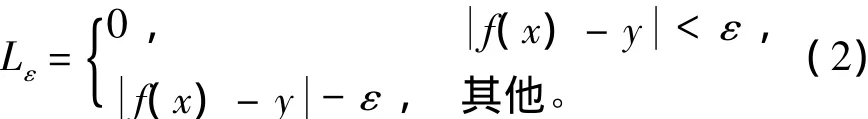
式(1)的求解转化为下式的最优问题求解

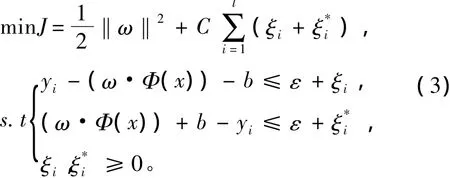
式中:ε为回归允许的最大误差;ξi和ξi*为松弛变量，C为惩罚参数。

式(3)的求解可以转化为Lagranage对偶问题求解

式中:аi和аi*定义为非负的Lagranage乘子，核函数定义为

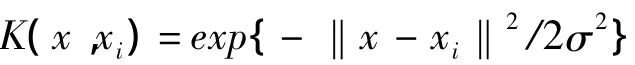
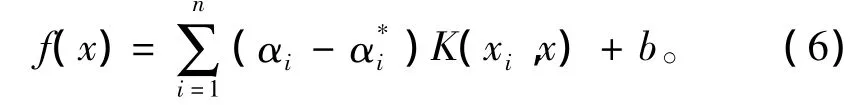
发动机的工作过程往往具有高度的非线性，考虑用支持向量机来辨识其动态行为，离散系统k +1时刻的输出可表示为:其中

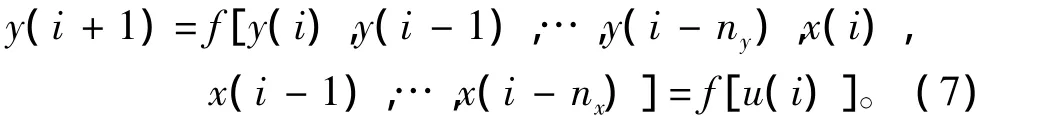
为建立支持向量机模型，首先构造训练样本［u(i)，y(i + 1)］。采用上述方法可将非线性的样本数据映射为高维空间的线性输出:

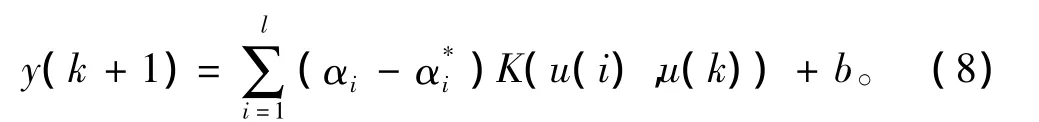
1.2PID参数整定

PID控制器的目标是产生控制信号u(k)能够在k + 1时刻使系统输出与参考模型输出的差值最小。因此构造目标函数

其中μ为惩罚系数，误差e定义为支持向量机模型预测的发动机输出yp与参考模型输出yr的差值

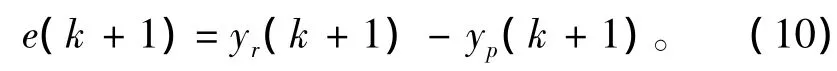
为改善控制过程的动态特性，引入参考轨迹。

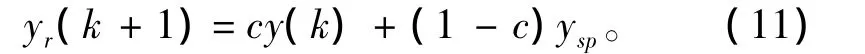
式中: y(k)为发动机实际输出; ysp为发动机输出的

目标值; c为可调参数(0＜c＜1)。

PID控制器参数整定问题则转化为寻找最优解kp，ki，kd，使得上述目标函数取最小值。本文采用粒子群算法来求解这一优化问题。粒子群算法的基本原理如下:在D维的目标搜索空间中初始化一群随机粒子，其中第i个粒子表示为一个D维向量Xi= (xi1，xi1，…，xiD)，i = 1，2，…，N，每个粒子的位置就是一个潜在的解。将Xi代入一个目标函数就可以算出其适应值，根据适应值的大小来衡量解的优劣。第i个粒子的速度也是D维向量，记为Vi= (vi1，vi1，…，viD)。第i个粒子迄今为止搜索到的最优位置称为个体极值pbest，记作Pi= (pi1，pi1，…，piD)，整个粒子群迄今为止搜索到的最优位置称为全局极值gbest，记作Pg= (pg1，pg1，…，pgD)。

PSO基于上述2个极值对粒子的速度和位置进行更新:

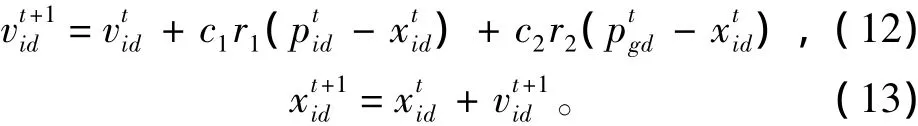
式中: i = 1，2，…，N，d = 1，2，…，D;学习因子c1和c2为非负常数; r1和r2为2个相互独立的在区间［0，1］上均匀分布的伪随机数。

粒子群算法流程如图2所示。

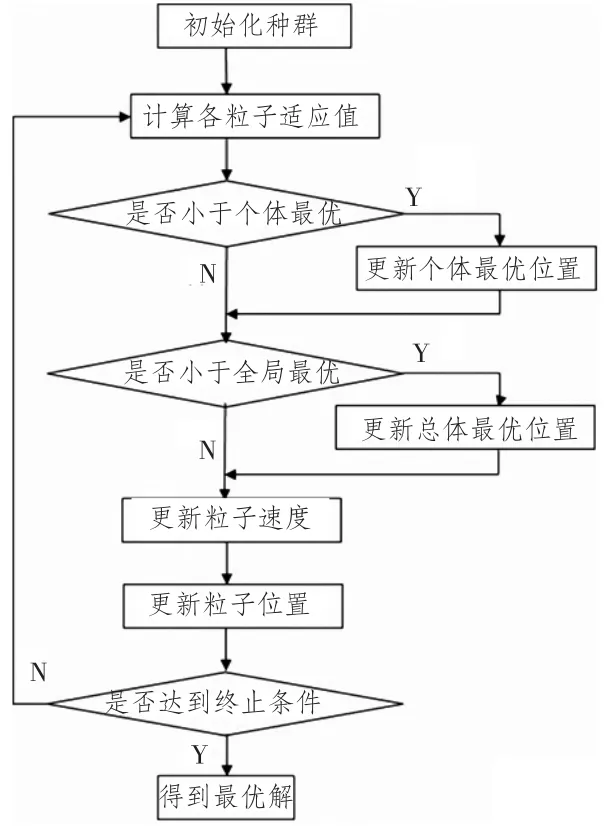
图2　粒子群算法流程图Fig.2　Flow chart of PSO algorithm

2　仿真研究

2.1发动机的辨识仿真

为了获得发动机的辨识模型，必须收集发动机的输入输出数据，用以对支持向量机进行离线训练。训练中采用1 000组信号，前500组作为学习样本用于训练支持向量机，后500组用于测试所得支持向量机的性能。支持向量机的设计参数为: C = 10，000，ε= 0.01，σ= 40。

支持向量机辨识仿真结果如图3和图4所示，其中图3为训练样本的拟合情况，图4为测试样本的拟合情况，图中的数据作了无量纲化处理。由图可知，支持向量机模型很好的拟合了训练和测试样本，表明支持向量机具有良好的辨识精度，经过训练过支持向量机能够准确描述发动机的动态行为。

图3　训练样本和支持向量机输出对比Fig.3 Comparison between training data and SVM outputs

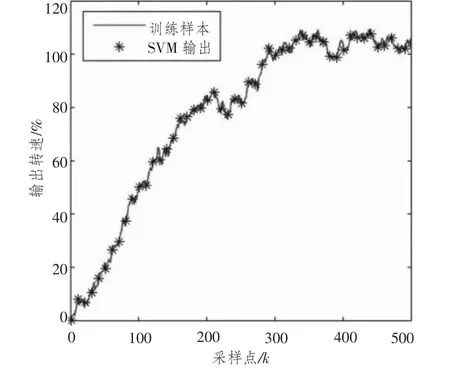
图4　测试样本和支持向量机输出对比Fig.4 Comparison between testing data and SVM outputs

2.2控制系统的仿真

控制系统仿真结果如图5和图6所示，其中图5为燃料供应量变化曲线，图6为发动机转速变化曲线，图中的数据作了无量纲化处理。从仿真结果可看出，基于SVM的参数自整定PID控制系统响应快速，系统调节时间约为2 s，且无超调，表明该控制策略可以很好地完成鱼雷发动机控制。

图7展示了采用粒子群算法的收敛曲线。由图可知，采用粒子群算法收敛至最小值只需要不超过

30步的迭代计算，表明该算法是一种高效快速的优化算法，可以满足实时控制系统的要求。

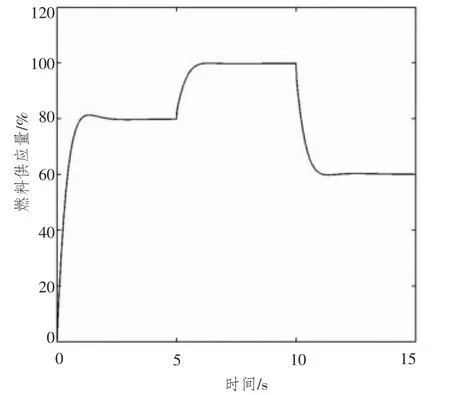
图5　燃油供应量的变化曲线Fig.5　Response of fuel flow rate

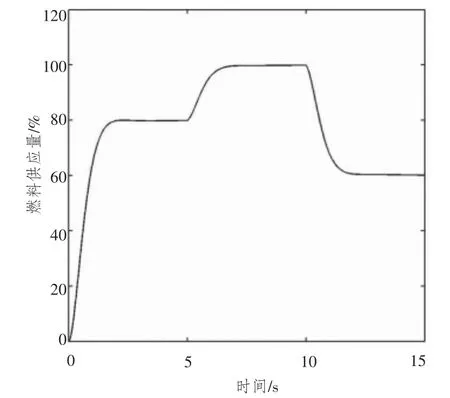
图6　发动机转速的变化曲线Fig.6　Response of engine rotation speed

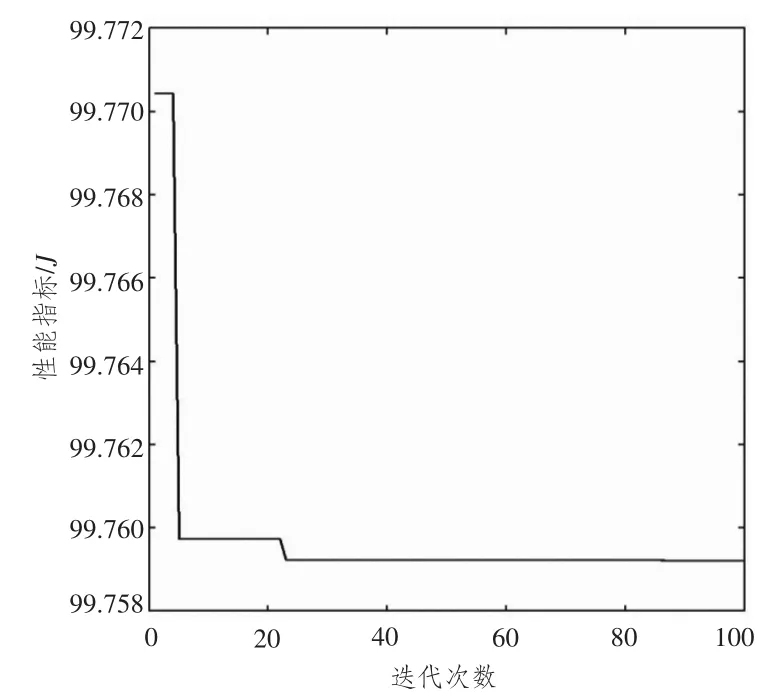
图7　粒子群算法的收敛曲线Fig.7 Convergence curve of PSO algorithm

3　结语

本文针对鱼雷发动机提出了基于支持向量机的参数自整定PID控制方法。与传统PID控制相比，参数自整定PID的控制效果对于初始的kp，ki，kd参数不敏感，只需使初始的kp，ki，kd参数在一定的合理范围即可，从而避免了精确整定PID参数的繁琐工作。仿真实验表明，支持向量机能很好地拟合发动机的动态特性，基于支持向量机的参数自整定PID控制器响应快速，无超调，控制效果良好。

参考文献:

［1］王伟，张晶涛，柴天佑．PID参数先进整定方法综述［J］．自动化学报，2000，26(3) :347－355．WANG Wei，ZHANG Jing-tao，CAI Tian-you．A survey of advanced PID parameter tuning method［J］．Acta Automatica Sinica，2000，26(3) :347－355．

［2］刘金琨．先进PID控制及其MATLAB仿真［M］．北京:电子工业出版社，2004．LIU Jin-kun．Advanced PID control and Matlab simulation ［M］．Beijing: PublishingHouseof Electronic Industry，2004．

［3］姚华，袁鸯，鲍亮亮，等．航空发动机神经网络自学习PID控制［J］．推进技术，2007，28(3) :313－316．YAO Hua，YUAN Yang，BAO Liang-liang，et al．Selflearning PIDcontrol based on neural networks for aeroengines［J］．Journal of Propulsion Technology，2007，28 (3) :313－316．

［4］李秋红，孙健国，周继超．航空发动机PID控制参数优化的改进遗传算法［J］．南京航空航天大学学报，2006，38 (2) :162－165．LI Qiu-hong，SUN Jian-guo，ZHOU Ji-chao．Improved algorithm for calculating GA Fitness function of aeroengine PID controller parameter optimization［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2006，38 (2) :162－165．

［5］VAPNIK V．The nature of statistical learning theory［M］．New York: Springer-Verlag，1999．

［6］SMOLA A J，SCHOLKOPF B．A tutorial on support vector regression［J］．Statistical Computation，2004 (14) : 199 －222．

［7］KENNEDY J，EBERHART R．Particle swarm optimization ［C］．Proceedings of IEEE International Conference on Neural Networks，1995:1942－1948．

［8］谢晓锋，张文俊，杨之廉．微粒群算法综述［J］．控制与决策，2003，18(2) :129－134．XIE Xiao-feng，ZHANG Wen-jun，YANG Zhi-lian．Overview of particle swarm optimization［J］．Control and Decision，2003，18(2) :129－134．

作者简介:路骏(1986－)，男，博士后，研究方向为水下能源动力技术。

基金项目:中国博士后科学基金资助项目(2014M552503)

收稿日期:2014－06－30;修回日期: 2014－08－20

文章编号:1672－7649(2015) 07－0108－04doi:10.3404/j.issn.1672－7649.2015.07.024

中图分类号:TJ630．1

文献标识码:A