基于改进BP神经网络的GPS信号反演蒸发波导研究

张海勇，陈立军，周　朋

(1．海军大连舰艇学院通信系，辽宁大连116018; 2．中国人民解放军91404部队，河北秦皇岛066000)

基于改进BP神经网络的GPS信号反演蒸发波导研究

张海勇1，陈立军1，周朋2

(1．海军大连舰艇学院通信系，辽宁大连116018; 2．中国人民解放军91404部队，河北秦皇岛066000)

摘要:海上蒸发波导的存在，对舰载通信、雷达等电子装备产生严重影响，蒸发波导的准确预测是保证舰载电子装备对波导有效利用的前提。研究基于神经网络利用GPS信号接收功率反演蒸发波导的算法流程，提出采用贝叶斯正则化训练方法改进的BP神经网络的方法原理和计算步骤，实现了对蒸发波导的仿真反演。仿真结果表明，贝叶斯正则化BP神经网络能够实时高效反演蒸发波导高度和大气修正折射指数剖面，且在存在干扰的条件下反演结果更为真实可信。

关键词:GPS信号;贝叶斯正则化; BP神经网络;蒸发波导反演

Inversion for evaporation duct using GPS signals based on improved BP neural network

ZHANG Hai-yong1，CHEN Li-jun1，ZHOU Peng2
(1．Department of Communication，Dalian Navy Academy，Dalian 116018．China; 2．No．91404 Unit of PLA，Qinhuangdao 066000，China)

Abstract:The existence of evaporation duct has severely influenced the electronic equipments，such as shipboard communications and radar，and so on．The accurate predication of evaporation duct is the presupposition of efficient using of duct by shipboard electronic equipments．This paper studied the inversion for evaporation duct using the received power of GPS signals which based on neural network，raised the principle and figure of improved BP neural network which is modified by Bayesian regularization algorithm．Stimulated the inversion for evaporation duct．The stimulation result shows: improved BP neural network can inverse the height of evaporation duct and the atmospheric modified reflection index on time and sufficiently，the inversion result under interference is more reliable．

Key words:GPS signals; bayesian regularization algorithm; BP neural network; inversion for evaporation duct

0　引言

目前，国内外对海上蒸发波导预测的研究主要集中在2个方面:一种是传统的以莫宁—奥布霍夫(Monin－Obukhov)相似理论为基础，基于气象水文参数预测蒸发波导的方法［1－6］;另一种是利用雷达或卫星数据反演蒸发波导的方法［7－9］。与传统的基于气象水文参数的蒸发波导预测方法相比，蒸发波导反演方法具有输入参量单一、易获取、反演速度快、时效性高等优点。与基于雷达海回波反演蒸发波导模型相比，基于GPS信号的反演方法不需要主动发射探测信号，只需要一个被动的海面信号接收机即可，设备简单、易行，并具有非常好的隐蔽性，适合军事通信的需求。人工神经网络是模拟大脑神经网络结构和功能建立的一种信息处理系统［10］，在反演的优化算法中，神经网络方法具有优良的非线性映射功能，在解决复杂的非线性问题上具有一定的优势，因此，本文采用贝叶斯正则化训

练方法的BP神经网络利用GPS信号接收功率反演蒸发波导。

1　GPS卫星系统简介及反演步骤

全球定位系统主要包括GPS卫星、地面监控系统以及GPS信号接收机三大部分。该系统设计的最初目的是用于目标的导航与定位，随着研究的深入，在环境与目标的遥感方面得到成功应用，在对流层蒸发波导反演中使用的GPS海面散射信号来自于低仰角的GPS卫星［11］。利用GPS信号反演蒸发波导是对波导高度的反演，因为蒸发波导大气修正折射指数模型是单参数模型，只要反演出波导高度即可以得到大气修正折射指数剖面，反演步骤如下:

1)蒸发波导参数建模。即构建合适的蒸发波导剖面模型，确定折射指数参数的维数。在构建模型时，认为折射指数剖面随距离的变化缓慢，可假定在水平距离上不变。本文采用P－J模式给出的单参数蒸发波导模型，该模型描述蒸发波导剖面准确，应用广泛，其表达式如下:式中: z0为海面粗糙度高度，通常取z0=1.5×10－4m; M(z0)为z0处的大气修正折射指数; d为蒸发波导高度。

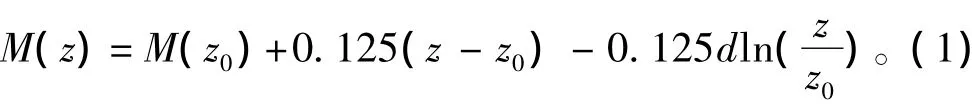
2)正向计算GPS信号接收功率。构建合适的GPS信号电波传播模式，根据步骤1中确定的波导传播模型，利用抛物线方程方法计算接收机接收到的GPS功率，在传播距离(r1，r2，…，rn)处进行离散，得到离散功率Pr。

利用抛物线方程可以有效计算电磁波在大气环境中的传播特征，求解基于GPS信号的抛物线方程过程中需如下初始场及边界条件:

①初始场计算公式:

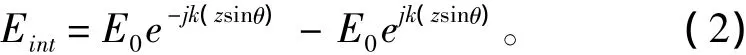
式中: E0为入射波的幅值; k为波数; z为垂直高度。

②上边界条件:处理上边界条件时，在每一步计算得到的场分布乘以如下窗函数，保证上边界区域内场分布缓慢。

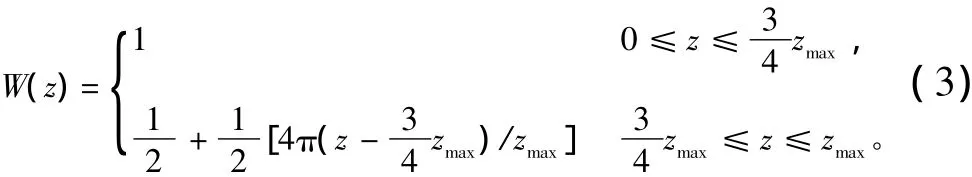
③下边界条件:求解抛物线方程时选取下边界(z = 0 )是平滑的理想导体平面，即下边界条件如下:

3)训练神经网络。将一部分离散功率Pr作为输入数据，所对应的蒸发波导高度作为目标数据对神经网络进行训练，得到训练好的神经网络。

4)反演波导高度。将另一部分离散功率Pr作为输入数据代入已训练好的神经网络中，反演输出蒸发波导高度。

5)误差检验。对反演高度与实际高度进行误差分析，以检验反演结果与实际的符合程度，如有必要，修改模型重新反演。

2　改进的BP神经网络

用反向传播算法进行训练的多层前行网络称为反向传播神经网络，简称BP网络，BP网络是一种具有3层或3层以上神经元的前向、有导师学习方式训练的神经网络。网络结构如图1所示，网络的第1层为输入层，最后1层为输出层，中间的若干层称为隐含层，相邻层之间通过权值连接。

图1　BP网络结构图Fig.1　BP network structure

神经网络的神经元是一个多输入、单输出且具有非线性特性的单元，ωji为连接权值，θj为神经元阈值，用bj表示，φ为神经元激励函数，BP网络的神经元激活函数包括双曲正切S型函数、对数S型函数、线性函数、阶梯函数和斜坡函数等，连接权值和阈值的初值一般在(－1，1)内随机取值。因此神经元输入、输出关系数学表达式如下:

BP网络的学习过程主要分为2个阶段:第1阶段是输入已知的学习样本，通过设置的网络结构和前一次迭代的权值和阈值，计算出各个神经元的输出; 第2阶段是对权值和阈值进行修改，从最后一层向前

计算各权值和阈值对总误差的影响，据此对各权值和阈值进行修改。2个阶段反复进行，直到收敛为止。

虽然BP网络理论依据充分，过程严谨并得到广泛的应用，但自身也存在一定的局限性，例如网络收敛速度慢，易于陷入局部极小点等问题，考虑到本文对蒸发波导的预测具有实时性或近实时性，且预测高度需满足一定的精确度，因此本文利用在BP网络基础上采用贝叶斯正则化训练方法的改进的BP网络。

贝叶斯正则化神经网络的一个最主要特点是增强网络的泛化能力。正则化是指为提高神经网络的泛化能力而限制权、阈值规模，通过修正神经网络的训练性能函数来提高其泛化能力［12］。

在一般情况下，神经网络的误差为:

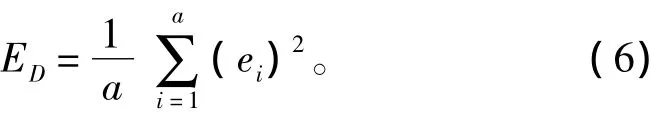
式中: a为样本对个数; ei为目标输出与实际输出的差值，正则化理论在误差基础上加入一个约束项，代表平滑性约束，这时目标函数为:

式中: Eω为网络权重的平方和;α和β为参数，用于控制权值及阈值的分布形式。在引入新的性能指标函数后，正则化方法在确保网络误差尽可能小的情况下尽量减少网络权值，有助于提高神经网络的泛化能力。

贝叶斯理论用来确定正则化参数α和β为大小，根据贝叶斯理论α和β的后验概率分布为:

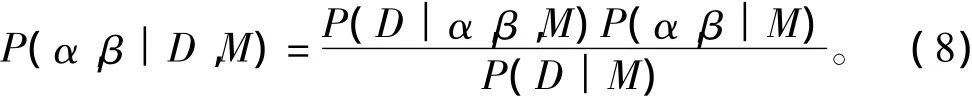
式中: M为隐层神经元的个数; D为样本数据集。

可以求得:

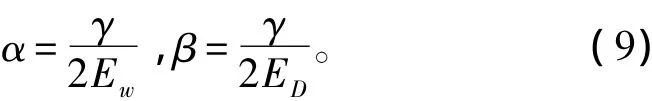
式中:γ为有效的网络参数数目，γ=N－2αtr(H)－1; H为目标函数的Hessian矩阵; N为网络的所有参数的数目。γ的取值范围为0～N，如果γ非常接近N，则说明网络的隐含层神经元个数己经足够大而可以正确表达网络输入参数和网络目标值之间的关系，当继续增大隐含层神经元个数时，且γ保持不变，则表明已获得了最优的网络结构及网络有效参数γ［13］。采用贝叶斯正则化训练方法的BP神经网络主要步骤如下:

1)设置网络结构，初始设定神经网络的隐含层数和连接权值，初始化网络参数α和β，为α和β赋予先验初值。

2)利用标准的BP算法训练神经网络，使总误差最小，并利用Hessian矩阵计算有效网络参数的数目γ。

3)利用式(9)计算优化正则化参数α和β。

4)对不同的参数初值重复以上3步，直到网络收敛为止。

3　蒸发波导的反演

根据蒸发波导的反演步骤贝叶斯正则化BP神经网络方法原理，研究利用GPS信号接收功率对蒸发波导进行反演。通过抛物线方程的正向出传播模型可计算得到不同距离处GPS信号接收功率，GPS卫星系统参数如表1所示。

蒸发波导大气修正折射指数模型是单参数模型，反演出波导高度即可以得到大气修正折射指数剖面，因此，本文将不同蒸发波导高度的GPS信号接收功率与其对应的波导高度作为神经网络训练的输入数据和目标数据。蒸发波导高度一般不超过40 m，目标数据选取高度从2～40 m，每隔2 m取一个波导高度，共20个采样高度;利用抛物线方程计算接收天线高度15 m处的GPS信号接收功率，输入数据选取距离从31～60 km以0.5 km为间隔的各点的接收功率，共59个采样频率。因此输入为59×20的不同距离和波导高度处接收功率矩阵，输出为1× 20的不同波导高度矩阵，以此输入输出来训练神经网络，神经网络参数如表2所示。

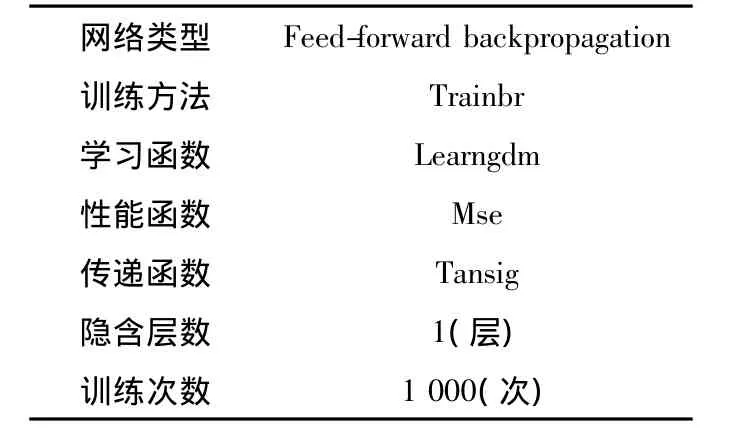
表2　神经网络参数Tab.2 Neural network parameters

训练神经网络共用时1'36″，网络实际训练次数为994次，即在训练994次之后网络已满足精度要求，网络训练过程均方差下降曲线如图2所示。

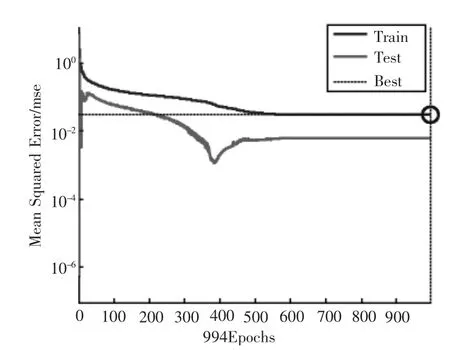
图2　Tainbr函数BP网络训练过程曲线Fig.2　The training process curve by trainbr function of BP network

以波导高度为15 m和25 m的GPS信号接收功率作为检验数据来验证反演的准确性，图3给出了波导高度为15 m和25 m时的GPS信号接收功率随距离的变化情况。

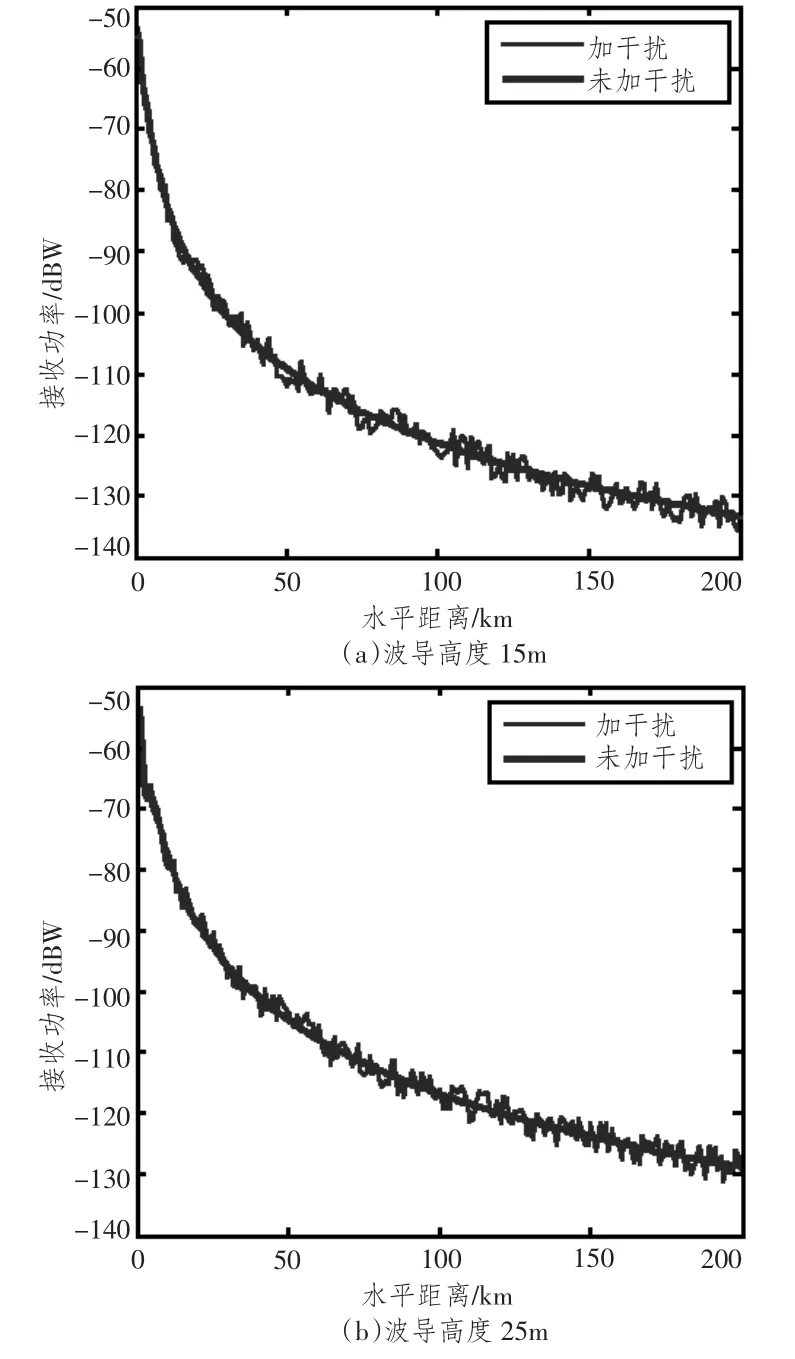
图3　GPS信号接收功率随传播距离的变化曲线Fig.3　The curve of GPS signal reception power with the propagation distance

图3给出了在没有干扰和含有干扰情况下不同波导高度条件下GPS信号接收功率随传播距离的变化曲线，虽然含有干扰的情况下GPS信号接收功率会发生振荡，对反演精度带来一定的影响，但其与实际情况更为相符。分别对上述情况的接收功率代入训练好的神经网络进行反演，反演结果如表3所示。

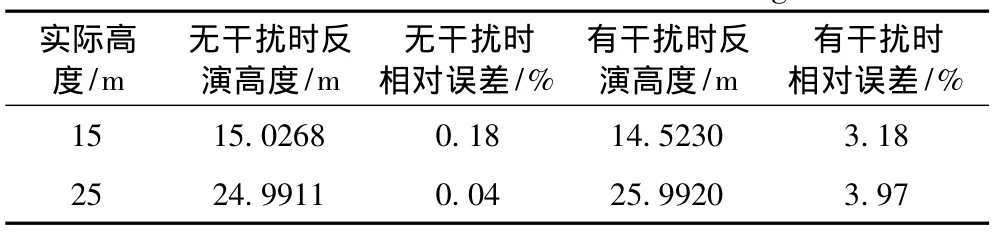
实际高度/m无干扰时反演高度/m无干扰时相对误差/%有干扰时反演高度/m有干扰时相对误差/% 15　15.0268　0.18　14.5230　3.18 25　24.9911　0.04　25.9920　3.97

蒸发波导高度反演结果表3所示，可以看出，在未加干扰的情况下，波导高度在15 m和25 m时，反演结果与实际结果相差不大，相对误差小于1%，反演精度较高;而在存在干扰的情况下，蒸发波导高度反演结果与实际值差距较大一些，相对误差在3%左右，但在可接受范围内，考虑到实际海洋气象环境下噪声等干扰是不可避免的，因此，在有干扰情况下的反演结果更可信。利用神经网络反演得到的大气修正折射指数廓线如图4所示，可以看出，在未加干扰情况下大气修正折射指数廓线与实际廓线几乎重合，而存在干扰情况下的反演结果更为真实。

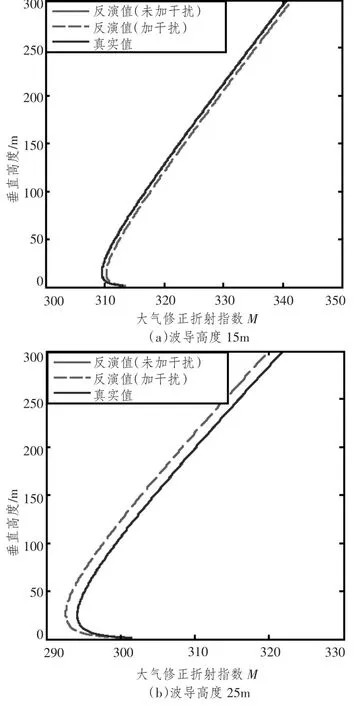
图4　蒸发波导大气修正折射指数廓线反演结果Fig.4　The inversion results of evaporation duct atmospheric refraction corrcction index profile

为进一步验证利用贝叶斯正则化BP网络反演结果的可信性，在其他条件不变的情况下，改变GPS卫星系统频率参数，以9 GHz频率的GPS信号接收功率来训练和反演蒸发波导，以波导高度23 m 和33 m时的接收功率来验证反演结果的准确性，反演结果如表4所示。

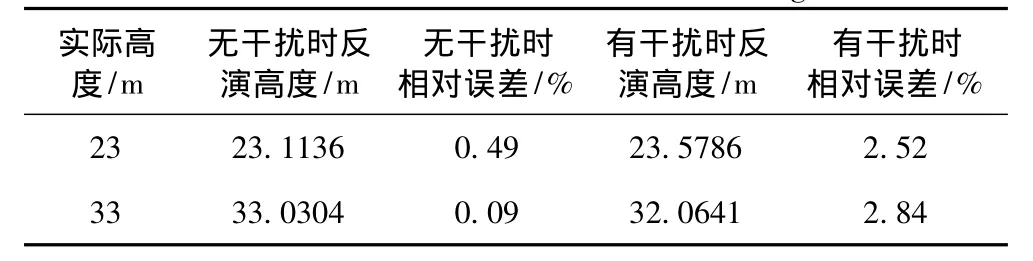
表4　反演高度计算结果Tab.4　The results of the inversion height

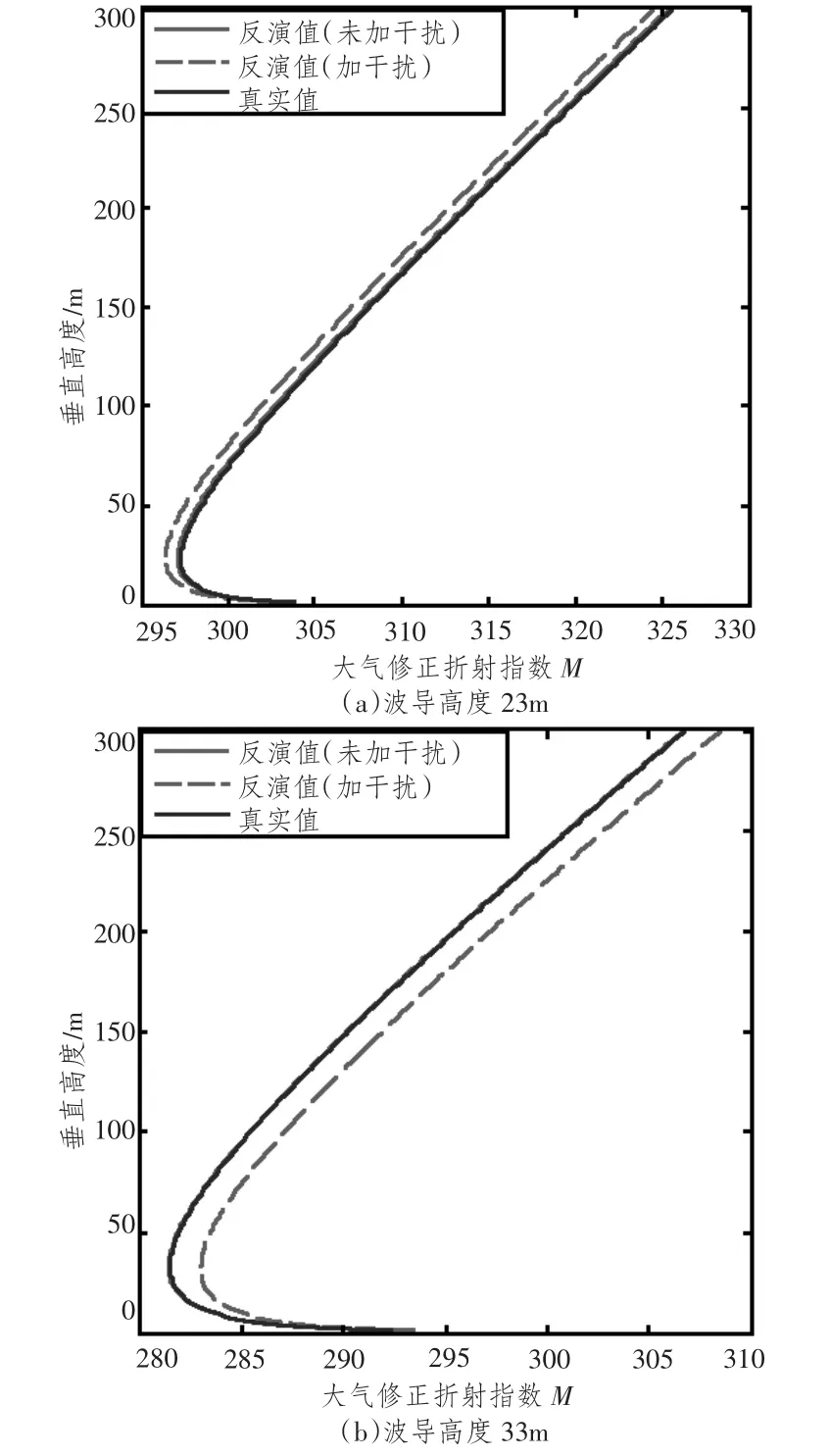
图5　蒸发波导大气修正折射指数廓线反演结果Fig.5　The inversion results of evaporation duct atmospheric refraction corrcction index profile

从表4和图5可看出，在GPS卫星系统频率不同的情况下，反演结果趋势相同，即在存在干扰条件下反演结果与实际情况更相符，可信度更高;同时，贝叶斯正则化BP网络对不同频率的GPS信号功率的反演具有较强的适应性。

综上所述，虽然在存在干扰的情况下利用贝叶斯正则化BP网络反演蒸发波导的反演结果的准确性较差于不存在干扰情况下的反演结果，但存在干扰情况下的反演结果与实际环境下的预测结果更为接近，并且反演结果误差均在可接受的范围内，说明利用贝叶斯正则化BP网络反演蒸发波导具备可应用性;从反演时间来看，每次神经网络的训练时间均在一分钟左右，与传统的基于水文气象环境预测方法的大量数据测量和计算相比，时间缩短程度较大，反演速度具有近实时性特点。因此贝叶斯正则化BP网络是一种适合舰载装备实时高效反演蒸发波导的方法。

4　结语

随着国内外对蒸发波导研究的深入，蒸发波导的反演问题逐步成为对蒸发波导预测研究的主要方向，本文基于海洋大气环境中蒸发波导存在特征，提出基于贝叶斯正则化训练方法的BP神经网络利用GPS信号接收功率反演蒸发波导的方法，仿真分析了蒸发波导条件下GPS信号接收功率随传播距离变化特征，分别在加入干扰和未加干扰的情况下利用检验数据对该算法进行了验证和蒸发波导的反演。反演结果表明，贝叶斯正则化BP网络能够反演出蒸发波导高度和大气修正折射指数廓线，在存在干扰情况下反演结果误差较大，但仍满足精度要求，且与实际情况更为相符，结果可信度更高。

参考文献:

［1］JESKE H．The state of radar-range prediction over sea．in Tropospheric Radio Wave Propagation．PartⅡ，1971: AGARD－CP－70．

［2］PAULUS R A．Specification for evaporation duct height calculations［D］．Naval Ocean Systems Center，1989．

［3］LUE Musson-Genon，GAUTHIER S，BRUTH E．A simple method to determine evaporation duet height in the sea surface boundary layer［J］．Radio Science，1992，27(5) :635－644．

［4］BABIN S M，YOUNG G S，CARTON J A．A new model of the oceanic evaporation duct［J］．Journal of Applied Meteorology，1997，36:193－204．

［5］刘成国，黄际英，江长荫，等．伪折射率和相似理论计算海上蒸发波导剖面［J］．电子学报，2001，29(7) :970－972．LIU Cheng-guo，HUANG Ji-ying，JIANG Chang-yin，et al．Modeling evaporation duct over sea with pseudo-refractivity and similarity Theory［J］．Acta Electronica Sinica，2001，29(7):970－972．

［6］李云波，张永刚，唐海川，等．基于海气通量算法的海上蒸发波导诊断模型［J］．应用气象学报，2009，20(5) : 628 －633．

［7］Yardim Caglar，Peter Gerstoft，WilliamS．Hodgkiss．Estimation of Radio from Radar Clutter Using Bayesian Monte Carlo Analysis．IEEE Trans，Antennas Propagate，2006，54(4) :1318 －1327．

［8］成印河，何宜军，赵振维，等．利用AMSR－E卫星数据反演蒸发波导高度的神经网络方法［J］．海洋技术，2008，27(4) :63－66．CHENG Yin-he，HE Yi-jun，ZHAO Zhen-wei，et al．BP Neural networks method for retrieval of ocean evaporation duct height from AMSR-E［J］．Ocean Technology，2008，27 (4) :63－66．

［9］王波，吴振森，赵振维，等．基于蚁群算法的需达海杂波反演蒸发波导研究［J］．电波科学学报，2009，24(4) :598－604．WANG Bo，WU Zhen-sen，ZHAO Zhen-wei，et al．Retrieving evaporation duct from radar sea clutter based on ant colony algorithm［J］．Chinese Journal of Radio Sience， 2009，24(4) :598－604．

［10］张治国．人工神经网络及其在地学中的应用研究［D］．吉林:吉林大学，2006．ZHANG Zhi-guo．Study on artificial neural networks and their applications in geoscience［D］．Jilin: Jilin Univeersity，2006．

［11］张金鹏．海上对流层波导的雷达海杂波/GPS信号反演方法研究［D］．西安:西安电子科技大学，2012．ZHANG Jin-peng．Methods of retrieving tropospheric ducts above ocean surface using radar seaclutter and GPS signals ［D］．Xi'an: Xi'an Electronic and Enginecring University，2012．

［12］ZHANG Xin-tao．WANG Yu，GAO Yong-sheng．Estimation of non-statistical uncertainty using fuzzy-set theory［M］．Meas．Se i．Technol，2000:430－435．

［13］李鹏．Bayesian算法在某运动轨迹测量仪中的应用研究［D］．哈尔滨:哈尔滨工程大学，2008．LI Peng．The application and research of Bayesian algorithm in a trajectory measuring meter［D］．Harbin:Harbin Engineering University，2008．

作者简介:张海勇(1966－)，男，博士后，教授，研究方向为通信与信息系统。

基金项目:国家自然科学基金资助项目(11374001)

收稿日期:2015－01－04;修回日期: 2015－01－26

文章编号:1672－7649(2015) 07－0073－05doi:10.3404/j.issn.1672－7649.2015.07.017

中图分类号:TP183

文献标识码:A