圆柱形基阵波束形成仿真研究

张雨强

(大连测控技术研究所，辽宁大连116013)

圆柱形基阵波束形成仿真研究

张雨强

(大连测控技术研究所，辽宁大连116013)

摘要:波束形成问题是阵列信号处理的核心问题。阵列的结构形状、阵元数目和处理算法等因素决定了其空域滤波的性能。本文给出圆柱形基阵的波束形成分解方法;然后深入研究圆柱形基阵的常规波束形成方法和旁瓣控制波束形成方法，通过利用圆阵的相位激励模式，将直线阵中应用的旁瓣控制加权方法应用到圆阵，从而降低圆柱形基阵输出的旁瓣级，以提高基阵性能;最后仿真分析圆柱形基阵在各种不同的加权方式下的性能。

关键词:波束形成;圆柱形基阵;波束形成分解方法;旁瓣控制

Simulation of the beamforming of cylindrical array

ZHANG Yu-qiang
(Dalian Scientific Test＆Control Technology Institute，Dalian 116013，China)

Abstract:The beamforming is an important issue in array signal processing．The spatial filter performance of the array is determined by the structure of the array number of the array element and processing algorithms．In this paper，a beamforming decomposing method of cylindrical array is introduced; and conventional sidelobe-controlled beamforming methods are deeply studied．By using the phased model of circular array，the sidelobe-controlled weighting methods of linear array can be applied to the circular array．As a result，the sidelobe level of cylindrical array is reduced，and the performance is improved greatly．Finally，the performance of different weightings of cylindrical array are simulated and analysised．

Key words:beamforming; cylindrical array; beamforming decomposing method;sidelobe-controlled

0　引言

阵列信号处理的一个至关重要的任务就是波束形成，其主要作用包括:形成基阵接收系统的方向性;进行空域滤波，抑制空间干扰与环境噪声，提高信噪比;估计信号到达方向，进行多目标分辨;为信号源定位创造条件;为目标识别提供信息等［1－2］。阵列的结构形状、阵元数目和处理算法等因素决定了其空域滤波的性能。均匀线阵在垂直方向上具有良好的指向性，但是，它在锥角相同的锥面上却存在着模糊，即不能分辨同一个锥面上不同的信号源［3］，对于均匀圆阵来说，虽然经过相移后在水平方向有较好的指向性，但它却不能分辨对称于圆阵所在平面分布的2个信号源，即在垂直方向上存在着模糊。并且均匀圆阵在垂直方向上的指向性本来就较差，所以，均匀圆阵不适合用于垂直方向上的波束形成，分辨垂直方向上的信号源。

圆柱形基阵的几何结构规则，同时兼备直线阵和圆阵的优点，在垂直方向和水平方向均具有指向性，消除了空间方位模糊，能够更好地抑制噪声和干扰，提高测量精度和测量增益。因此，本文从圆柱形基阵的阵列结构和波束形成基本理论出发，给出圆柱形基阵波束形成的分解方法，将圆柱形基阵的波束形成分解为水平方向波束形成和垂直方向波

束形成;然后再通过相位模式激励方法［4］，将直线阵中常用的旁瓣控制波束形成方法应用于圆阵;最后得到圆柱形基阵的旁瓣控制波束形成，并且对这些波束形成方法进行仿真分析，得出这些波束形成方法各自的性能以及它们在波束宽度和旁瓣级上的差异。

1　圆柱形基阵波束形成的分解

对于圆柱形基阵而言，实现波束形成所需的阵元数目众多，无疑增大了波束形成器的设计负担和处理负担，显然，需要研究提高计算效率的波束形成方法。一种行之有效的解决方案是从圆柱形基阵的几何结构出发，依据乘积定理对波束形成过程进行分解［4－5］。下面将进行详细描述。

首先，建立圆柱形基阵的阵列模型如图1所示。

图1　圆柱形基阵几何结构示意图Fig.1　Geometric configuration of cylindrical array

那么圆柱形基阵的频率－波束响应可以表示为

式中: (θ，φ)为平面波的波达方向; (θs，φs)为基阵的指向方向; N为圆阵个数; M为每一个圆阵上的阵元数; R为圆阵半径;φm为第m个阵元与x轴的夹角;λ为入射平面波波长;为第nm个阵元的加权值。

显然，上式中的第1项为直线阵的波束方向图，而第2项则恰为第n个圆阵的波束方向图。即柱形阵的波束方向图为直线阵的波束方向图和圆阵的波束方向图的乘积，则式(3)可化简为

式中: Blin(θ，φ)为直线阵波束方向图; Bcir(θ，φ)为圆阵的波束方向图。

从以上分析可知，在可分离加权的情况下，圆柱形基阵的波束形成可以分解为2步，如图2所示。这2步的波束形成处理在阵列理论中最为常见。第1步是对包含有M个全向阵元的N个圆阵进行波束形成;第2步将第1步输出的N个波束在z方向进行波束合成，即圆阵(对0°～360°方位角的估计)和直线阵(对0°～180°俯仰角的估计)波束形成［7－8］。这种分解使得三维空域窗的设计与合成变得更为简单。非均匀的加权窗函数也可以应用于每个圆阵的波束形成，以提高基阵对特定方位角φ的角度响应。均匀加权窗函数可以应用于直线阵的波束形成，来提高基阵对特定俯仰角θ的角度响应。

通过图2所示的波束形成分解，圆柱阵波束形成器的计算结构得到大大简化，所有参与波束形成的直线阵和圆阵可以并行执行，并且通过使用文献［4］中所述相位模式激励方法，现有高效的直线阵和圆阵波束形成器优化设计方法均可以移植过来。

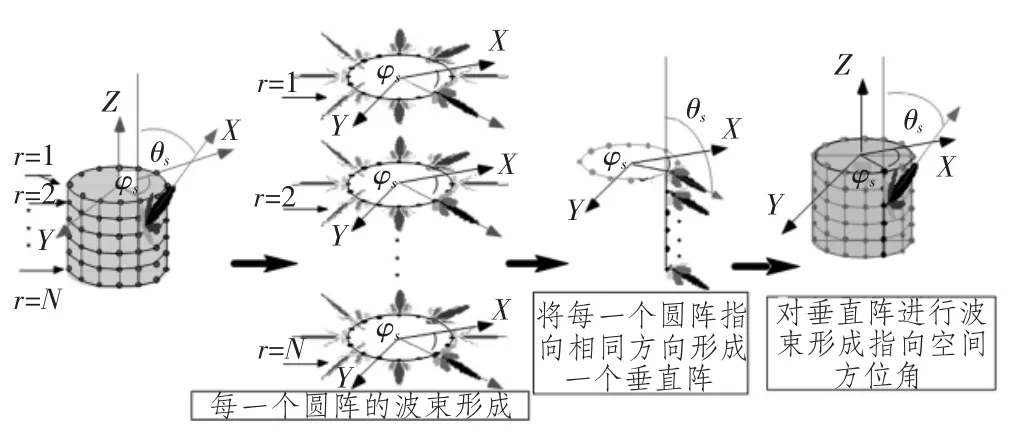
图2　圆柱形基阵波束形成的分解及合成Fig.2 Decomposition and synthesis of cylindrical array beamforming

2　仿真分析

圆柱形基阵的几何如图1所示，假设阵元数T =

N×M = 12×15 = 180;基阵设计频率为f0= 4 kHz，阵元间距d = ds =λ0/2，d为相邻圆阵之间的距离，ds为同一圆阵上相邻阵元之间的距离，λ0为设计频率所对应信号波长。对基阵的波束图进行仿真如下。

2.1均匀加权

对基阵的水平方向和垂直方向都使用均匀加权，水平方向权值通过相位模式激励方法求得，垂直方向权值利用均匀加权求得。假设基阵指向方向为正侧向，即(θs，φs) = (90°，0°)。利用式(3)得到均匀加权波束方向图如图3所示。

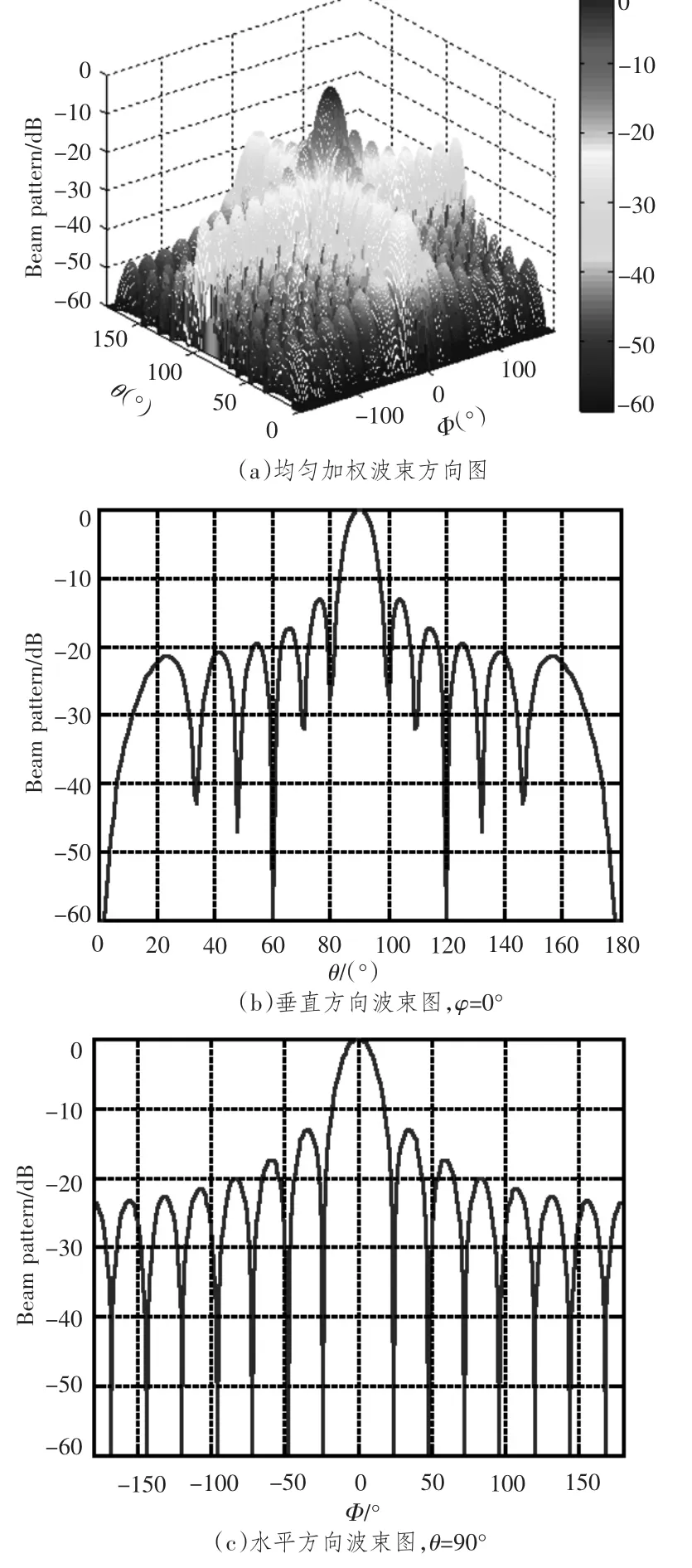
图3　波束图Fig.3　Beam pattern

从图3中可看到，采用相位模式激励后，圆阵在水平方向上也有与线阵相似的波束图。当然，我们也可以对圆柱形基阵的波束图进行调向，假设基阵的指向方向为(θs，φs) = (80°，10°)，则可得到波束方向图如图4所示。

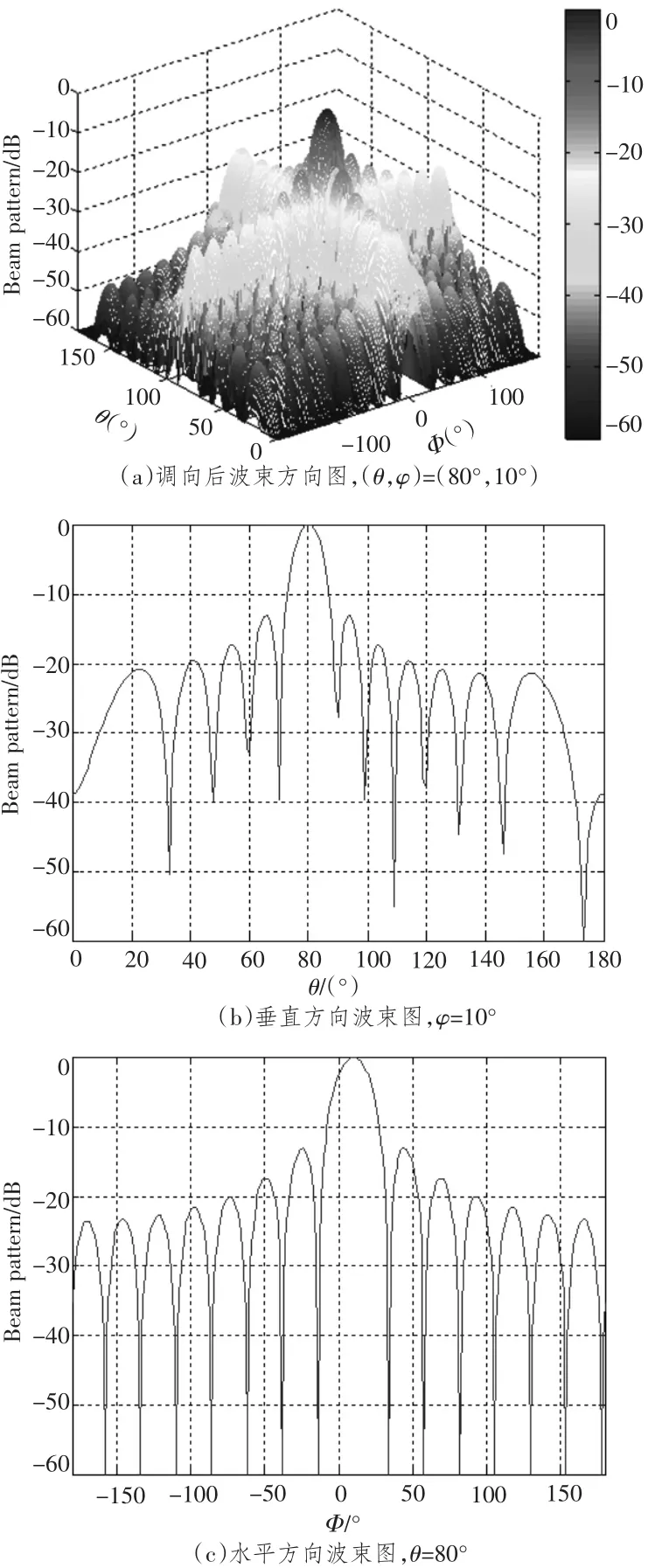
图4　波束图Fig.4　Beam pattern

根据图3和图4可得，垂直方向和水平方向的波束宽度及旁瓣级如表1所示。

从表1可看出，调向后垂直方向上的波束宽度变宽，偏离水平方向越大，波束宽度越宽，而对旁瓣级的影响却不是很大;在水平方向上，调向前后的波束宽度和旁瓣级不变，这与圆阵的对称性有关，圆阵在各个方位角的分辨力相同［6］。

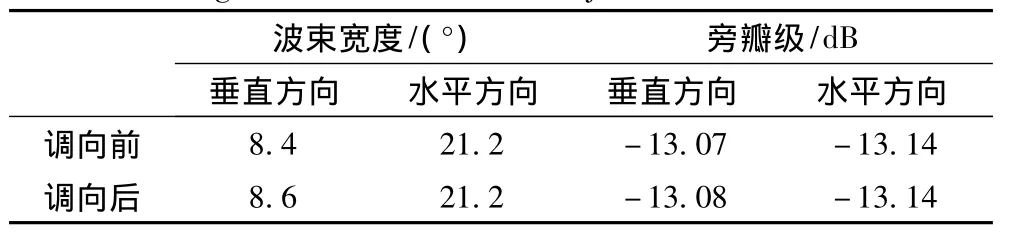
表1　均匀加权调向前后波束宽度和旁瓣级对比Tab.1　The contrast of beam width and sidelobe with uniformweigthed before and after adjusted

2.2垂直方向和水平方向均为Dolph-Chebyshev加权

均匀加权是阵列处理中最简单的加权方法，可以获得最大的阵增益，但是，均匀加权的旁瓣级过高，极限高度为－13.5 dB，这在工程实际中是不能被接受的，下面使用能获得恒定旁瓣级的Dolph-Chebyshev加权对圆柱形基阵进行波束图仿真，设计波束旁瓣级为－20 dB。

图5　波束图Fig.5　Beam pattern

由图5可见，使用Dolph-Chebyshev加权后，水平方向和垂直方向的波束图都有恒定不变的旁瓣级，这也是Chebyshev加权在很多阵列中都有应用的原因。旁瓣级的降低必然会导致波束宽度的变大。

2.3垂直方向Dolph-Chebyshev加权，水平方向Taylor加权

实际应用中，我们可能需要衰减的旁瓣形状，此时可以使用前面介绍的Taylor加权和Villeneuve加权。在垂直方向上，相当于直线阵的波束形成，此处还继续使用Dolph-Chebyshev加权，只在水平方向使用Taylor加权求取权值。仿真波束图如图6所示。在水平方向上获得－20 dB的旁瓣级和衰减的旁瓣。

图6　波束图Fig.6　Beam pattern

2.4垂直方向Dolph-Chebyshev加权，水平方向Villeneuve加权

Villeneuve加权和Taylor加权区别不大，只在阵元数较少的情况下有微小的差别，在大多数的应用中我们倾向于使用Villeneuve加权。在水平方向使用Villeneuve加权的波束方向图如图7所示。

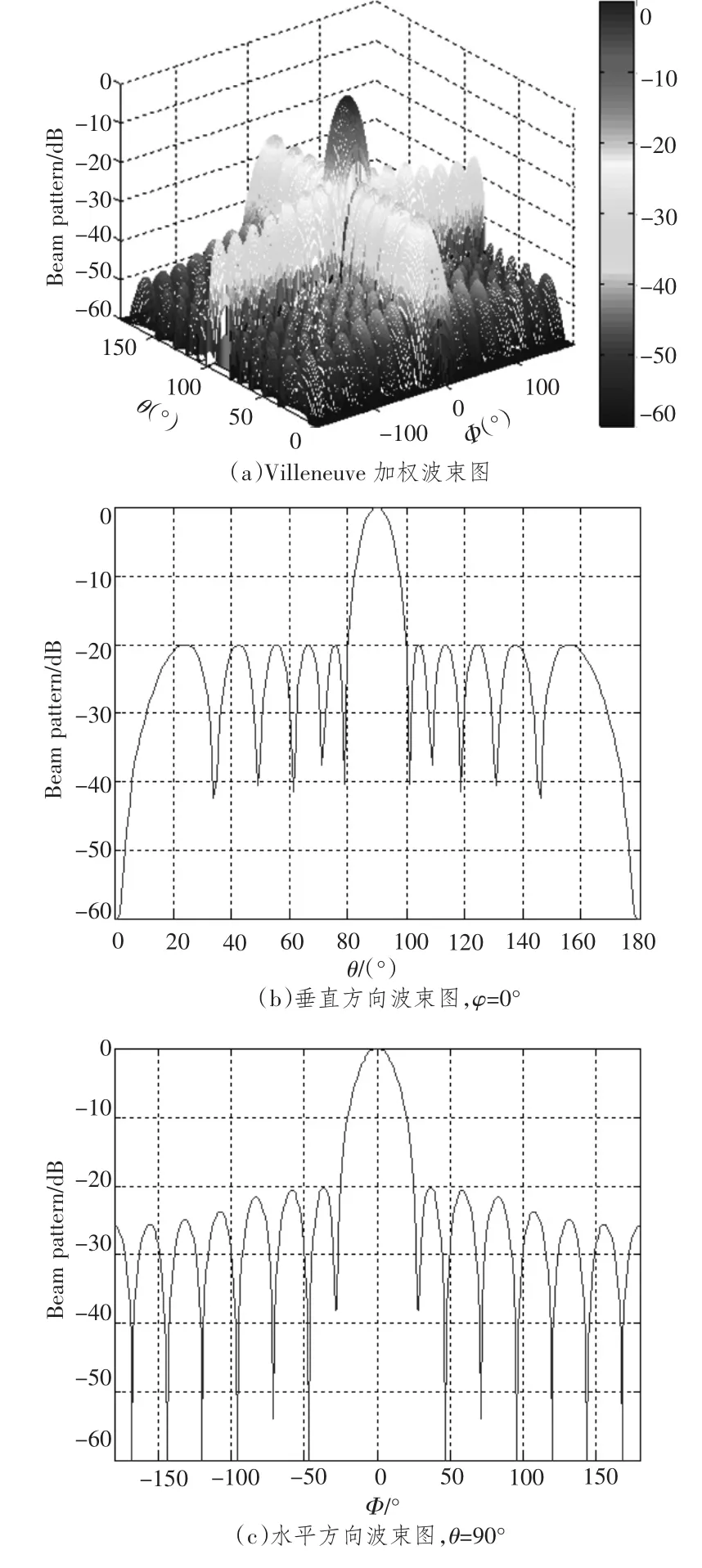
图7　波束图Fig.7　Beam pattern

综合上述仿真结果，为方便对比，表2列出了上述几种加权方法所得波束宽度和旁瓣级。通过对比易知，旁瓣级的降低必然导致波束宽度的变宽，同时，在使用旁瓣控制加权方法时，在垂直方向和水平方向都能达到想要的理想旁瓣级。

表2　不同加权方法的波束宽度和旁瓣级对比Tab.2　The contrast of beam width and sidelobe betweendifferent weightings

3　结语

本文首先给出圆柱形基阵的结构形式，依据乘积定理，给出了圆柱形基阵的波束形成分解方法，即圆柱形基阵的波束形成可以分解为线阵波束形成和圆阵波束形成两部分。然后，深入研究了圆柱形基阵的常规波束形成方法和旁瓣控制波束形成方法，通过利用圆阵的相位激励模式，将直线阵中应用的旁瓣控制加权方法应用到圆阵，从而降低圆柱形基阵输出的旁瓣级，提高了基阵性能。最后，对圆柱形基阵波束形成器进行了计算机仿真，对基阵波束图的性能参数如波束宽度、旁瓣级等进行详细的讨论。由于圆柱形基阵参与波束形成的阵元数众多，而且实际应用中也存在着诸多的不确定因素，因此，结合实际应用，探索更适用于实际环境的波束形成方法，是我们今后需要进一步开展的工作。

参考文献:

［1］ALAN A．WINDER．Sonar system technology［J］．Ieee Tra-nsactions on Sonics and Ultrasonics，September，1975，22(5):291－332．

［2］MURAT GüREKEN．Neural network based beamforming for linear and cylindrical array applications［D］．Middle East Technical University，2009．

［3］KIRSTEINS I P，HONGYA G．Robust adaptive beamforming of volumetric arrays［J］．IEEE，2007:1247－1251．

［4］HARRY L．VAN T．最优阵列处理技术［M］．汤俊，等译．北京:清华大学出版社，2008，1．

［5］NEIL J．MALLOY．Array manifold geometry and sparse volumetric design optimization［J］．IEEE，2007:1257－1261．

［6］WAITE A D．实用声呐工程［M］．王德石，等译．北京:电子工业出版社，2004．

［7］TAWFIK A．A generic processing structure decomposing the beamforming process of 2－D＆3－D Arrays of sensors into sub-sets of coherent process［A］．16thNational Radio Science Conference，NRSC＇99．Ain Shams University，Cairo，Egypt．1999．

［8］Stergios Stergiopoulos．Advanced Beamformers［R］．Defence R＆D Canada-Toronto，Technical Report．2008．

作者简介:张雨强(1986－)，男，工程师，研究方向为阵列信号处理。

收稿日期:2014－10－13;修回日期: 2015－03－23

文章编号:1672－7649(2015) 07－0064－05doi:10.3404/j.issn.1672－7649.2015.07.015

中图分类号:TP183

文献标识码:A