配网重构与电容配置的改进模型及优化算法

蔡 浩，朱熀秋

(江苏大学电气信息工程学院，江苏镇江 212013)

网络中功率损失一直是配电结构和设备须首要考虑的问题.在传统方法中，优化重构和电容配置是应用在网络中降低网损和提高电压质量的两个有效方法.网络重构是通过改变开关状态来改变配电网络拓扑结构的过程.开关有分(N.O.)、合(N.C.)两种状态，在重构过程中，根据所提出的目标函数优化改进开关状态，通过开关的分、合操作控制网络中的有功流和无功流，降低功率损耗;电容器主要用于配电网络的功率补偿，通过优化配置电容器，达到降低功率损耗和改善电压分布的目的.

较多的文献独立研究了网络重构和电容器优化配置的问题，使用了多种方法和目标函数建立网络模型，并提出优化方案.文献［1］所提出的启发式搜索的近似求解方法被用于解决功率损耗最小的配网重构问题.该方法中，所有的网络开关先闭合，然后再逐一断开，形成一个新的辐射状结构.在文献［2］中，降低功率损失的问题和负载平衡重构问题构成了一个整数规划方法.文献［3］提出了支路交换启发式算法，通过闭合一个开关，导开另外一个开关，使得功率损耗降低.在提出数学优化方法的同时，较多学者研究了网络重构的人工智能算法，包括基于模糊多目标的遗传算法(GA)［4］、二进制粒子群优化算法(BPSO)［5］、蚁群搜索算法(ACSA)［6］等.此外，通过运算比较，结果表明蚁群搜索算法(ACSA)优于遗传算法(GA)和模拟退火算法(SA)［7］.

电容器优化配置的问题也是研究的热点.文献［8］构建了非线性规划模型，提出了一种改进的梯度搜索迭代程序的方法.通过分解法和潮流算法求解，将电容配置问题模型化，变为混合整数非线性规划问题.文献［9］认为选择合适数量的电容器是解决配置问题的关键所在，可使用遗传算法和一种新型的敏感性分析法的方法来解决.文献［10-12］采用综合进化算法求解电容器优化配置问题，该算法以差分进化和模式搜索作为启发式的优化工具，实现了年运行成本降低的目标.

一些研究同时考虑网络重构和电容配置的问题.在文献［13］中，电容器优化配置和配网重构被认为是两个连续的阶段，将支路交换法用于重构过程.文献［14］运用模拟退火算法(SA)解决电容器优化配置和配网重构，而电容量的大小由离散优化算法确定.文献［15］以功率损耗最小化为目标，同时解决了配置与重构这两个问题，结果表明蚁群搜索算法(ACSA)优于模拟退火算法(SA)和遗传算法(GA).文献［16］导出一种改进的粒子群优化算法，建立了特定时期内功率损耗最小化和成本降低的目标函数.在先前的研究中还能找出一些寻求局部最优或全局最优的方案.并且，所提出的每一种方法都试图找到最优或接近最优的解决方案.

文中提出一种新的改进的二进制粒子群算法，使得配网重构和电容配置实现同步优化.该方法克服以往研究中粒子传递和位置更新方面的缺陷，以降低网损为目标函数，采用不同的结构优化算法(使用逻辑运算符:AND，OR和XOR)，实现接近全局最优的网络重构和电容器配置.对某个IEEE16节点配电网络系统，在MATLAB R2010软件环境中编写优化算法，找到实现网损最小的配网重构和电容配置的方法.

1 数学模型及优化算法

1.1 问题描述

配网重构目标是网络损耗最小，考虑到特定负载模式下的约束条件，问题的数学模型表示为［17］

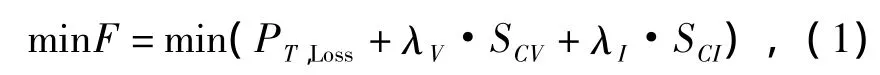
式中:PT，Loss为实际的网络总功率损耗;参数λV和λI为惩罚因子;SCV为违反电压约束的平方和;SCI为违反电流约束的平方和.式λV·SCV+λI·SCI是用于约束的目标函数，每个节点的电压幅值必须在允许区间内.此外，各支路的电流必须满足支路电流限制，这些限制区间如下:

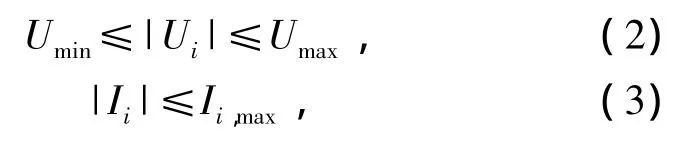
式中:|Ui|为节点I的电压幅值;Umin和Umax分别为允许电压的最小值和最大值，Umin=0.95 pu，Umax=1.05 pu;|Ii|为电流幅值;Ii，max为支路i的最大电流值.因此，惩罚因子表示如下:

1)若相关的电压/电流约束未被违反，则λV和λI=0.

2)若相关的电压/电流约束被违反，赋予λV和λI重要值，这使得目标函数重返正常的解决方案.该重要值等于目标函数优化前的值(测试网络的初始功率损耗)乘以一个较大的数(如104)，该计算过程由程序自动完成.

为研究配电网的功率损耗和电压变化，在优化过程中进行潮流计算.因配电网是辐射型结构，具有较高的R/X，使用高斯-赛德尔和牛顿-拉夫逊这两种传统的潮流计算得到的解决方案并不可靠.因此，文中研究了一种正倒向随机的潮流法(BF潮流)［18］.

1.2 正倒向随机的潮流法

BF潮流通常被用于问题的目标函数模型的评估.BF潮流计算中，第一步是将配电网拓扑结构导入计算机程序.主程序运行步骤如下:

式中:k为迭代次数;∈是估算误差(精度).

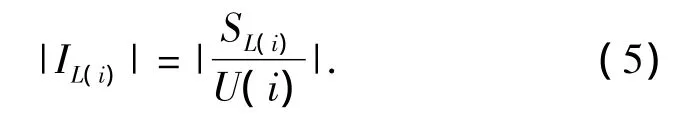
式中:IL(i)，SL(i)和U(i)分别为电流、视在功率和节点i的电压.

3)最后一个节点的电流是上支路电流.使用基尔霍夫电流定律(回代)从最后一个节点开始到第一个节点计算网络支路电流(J1×f)，f为网络分支的数量.

4)利用方程LU=ZJ计算电压降.Z为阻抗，LU1×f为各支路的电压降.

1.3 改进二进制粒子群优化

二进制粒子群优化(BPSO)算法是由甘乃迪(Kennedy)和艾伯哈特(Eberhart)在1997年提出的［19］.在一个标准的 BPSO算法中，优化过程使用了实数.该算法类似于标准的基本PSO算法，一个随机方法产生一个新的群，在标准模式下使用建立的关系计算粒子的速度，然后将计算速度与一个随机数比较，得到新的粒子位置0或1.该方法有两个缺点:一是从以前的迭代得到的粒子的信息不会用于下一次迭代;二是粒子位置的随机更新会产生不准确的结果.因此，引入改进BPSO算法［20］.

在改进BPSO算法中，迭代的每一粒子的信息被用于确定新的粒子.因此，如果每颗粒子包含d维(变量)，迭代k+1次，则

式中:“⊗”、“⊕”和“+”分别表示运算符“XOR”、“AND”和“OR”;w1和w2是惯性权重因子变量，为随机二进制字符串;为粒子i迭代k+1次时在d维的速度和分别表示粒子i到k次迭代的单体最佳位置的第d个维度，群中所有粒子k次迭代的最佳位置的第d个维度.每个粒子的新位置由等式(7)更新如下:

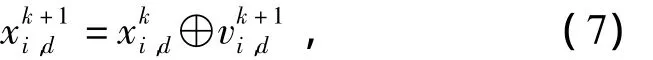
2 优化算法设计

为解决网络重构和电容器配置优化的问题，实施改进BPSO算法的步骤如下:

1)程序的输入为w1和w2，群的大小(P)，目标函数和最大迭代次数.

2)启动程序，生成包含随机二进制字符串初始种群.每个粒子群表示开/关的状态，安装在每个节点的电容器的状态以及所安装电容的容量.因此，如果决策变量的数量(搜索空间的维数)为N，则初始群为一个P×N阶矩阵如下:

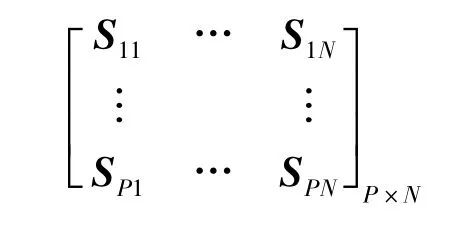
其中矩阵S由特别的编码程序构建而成，S中的每行是搜索空间飞行的一个粒子.

如上所述，每颗粒子由3部分组成:开关状态ON/OFF;安装在每个节点电容器的状态;所安装的电容器的容量.3个变量分别表示如下:switch-con，cap-con和cap-siz.

在switch-con中，二进制字符串的长度为r1+r2，其中r1是常闭开关的数量，r2是联络开关的数量.每一个分支都可以被认为是一个潜在的开关，可打开或关闭.开关的打开和关闭分别表示为0和1.

在cap-con中，所需的位数(r3)等于系统的节点数.节点上安装一个电容器，用1来表示.若一个节点上没有电容，则相应的位为0.

在字符串第3部分cap-siz中，字符串的长度等于节点(r3)的数量和电容器的编码比特数.例如，(001)2到(110)2是型号为1到6的6种不同电容的二进制数，比特数是3.因此，在一个16节点的网络中，cap-siz是一个48位字符串.

最后，cap-siz和cap-con位相乘，确定电容的位置和容量.一个典型的随机粒子串如图1所示.

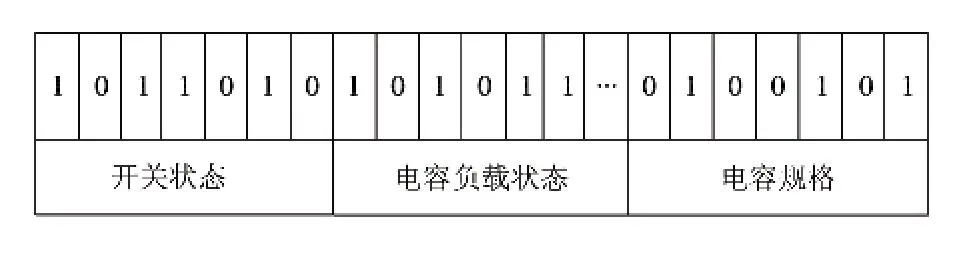
图1 随机典型粒子串

3)在每次迭代中验证网络辐射条件.该函数验证2种主要条件:网络中必须包含无环网络;所有的节点必须通电(连接电源).因此，该程序认为辐射状网络是一个初始图状树，上述条件验证了网络仍然是相同状态下的树.也就是说，如果网络图是树形，网络就保持辐射状.验证之后，在新生成的网络中进行潮流计算，重新计算节点电压和支路电流.在该步骤中，还需检查适用于目标函数式(1)的约束条件.

4)每次迭代计算更新了全局最优(pbest)和个体最优(gbest).它们是生成最小数量的目标函数的字符串.继续运行程序，直至达到最大预定数量的迭代次数.最后计算出的gbest是全局最优的网络状态，与其对应的功率损耗也是最佳的.

3 算例分析

使用文中提出的二进制粒子群优化算法，在IEEE16节点测试系统中进行配网重构和电容配置的综合优化计算.以该系统为基准，在 MATLAB R2010软件环境中编写本算法，将执行结果与先前研究得出的优化结果进行比较.在电容器配置中，使用 6 种类型的电容器(300，600，900，1 200，1 500 和1 800 kvar)，电容器的编号从1到6，0表示节点无任何电容，它们的等效二进制数如表1所定义.

表1 电容等效二进制数

3.1 仿真结果

为进一步验证算法的有效性，采用3条馈线的16节点系统进行分析，该配电网系统如图2所示，13条连续线代表常闭开关，常开开关(联络开关)15，21和26是用虚线表示，最初的网络损耗功率为509.89 kW［21］.

16节点测试系统的优化运算结果详见表2.网损降低了13.85%，5种型号电容器(1 500，900，1 800，900 和 900 kvar)分别被放置在节点 4，7，8，9和13.

图2 16节点的配电网系统

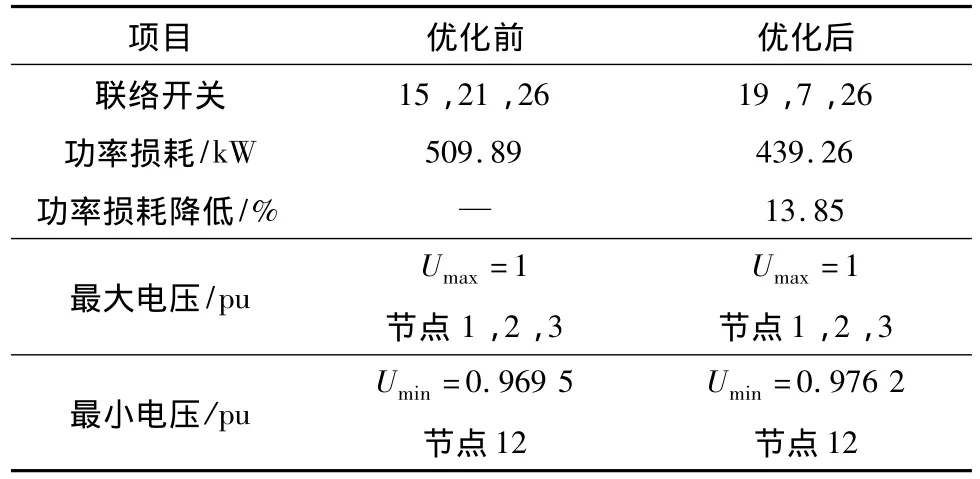
表2 16节点系统优化结果

网络重构和电容器配置前后电压分布的变化如图3所示，蓝线代表优化前，红线代表优化后.由图可见，优化后电压分布明显改善.

图3 16节点系统优化前后电压分布的比较

3.2 方案比较

在类似的负载、电压和电流等约束条件下，通过比较文中的优化算法和其他智能方法的研究结果，发现文中提出的算法获得了更好的结果.为验证损耗降低的结果，提出同时或单独进行网络重构和电容器配置的5个不同方案，方案参数详见表3和4.

方案1:仅配网重构;

方案2:仅电容器配置;

方案3:先配网重构再电容器配置;

方案4:先电容器配置再配网重构;

方案5:同时进行配网重构与电容器配置.

表3 16节点系统不同优化方案比较

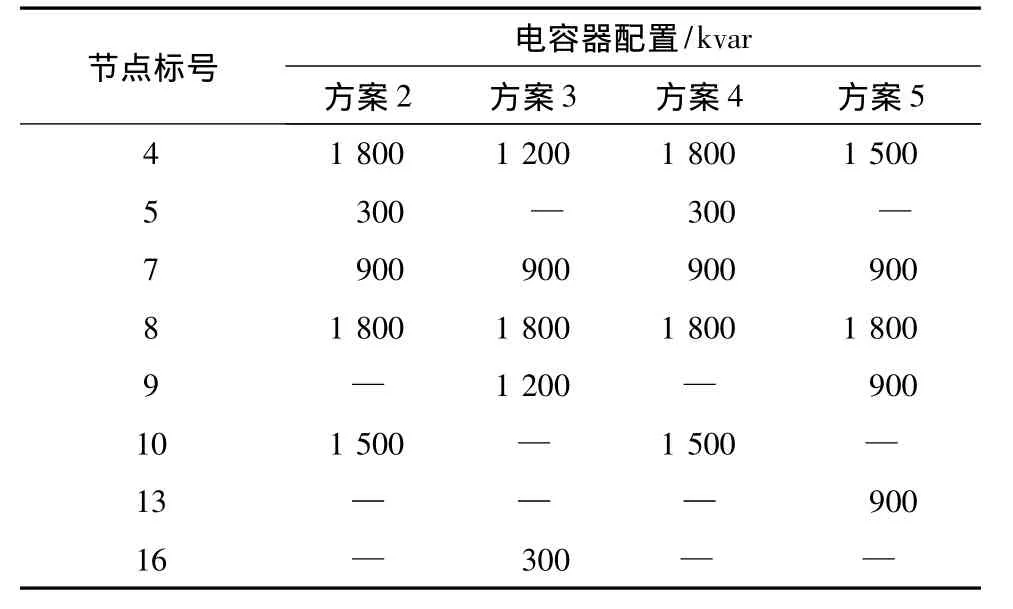
表4 16节点系统电容器配置方案比较

在方案5中，同步进行配网重构和电容器配置得到了最佳的网络状态.重点对方案3，4与5进行比较，根据表3中功率损失降低的计算结果，这3个方案实施的优先顺序如下:

1)方案5，网络重构和电容器配置同步进行;

2)方案3，先开展网络重构，然后配置电容器;

3)方案4，先配置电容器，再重构网络.

4 环境效益

我国的能源消费模式是以不可再生的常规化石能源为主，电厂发电排放出大量的CO2，SOx和NOx等污染物.功率和能量损失导致了有效发电量的降低，配电网本身也产生一定比例的功率和能量损失.因此在节能减排的环境下，探索和研究有效减小损耗的方法非常紧迫.传统的发电厂每兆瓦小时发电量所产生的排放量相当于720 kg CO2，，0.1 kg NOx和 0.003 6 kg SO2［22］.文中提出配网重构和电容配置同步优化的方法能显著降低配电网损耗量和污染物排放量.年能量损耗减少量如式(8)所示:

式中LF为损失系数，假定所有负载为民用，则LF=0.3.16节点测试系统计算结果显示，年能量损耗减少185.616 MW·h，CO2，NOx和SO2排放分别减少133 643.52，18.56 和0.67 kg.

5 结论

在配电网中同步优化重构和电容器配置，实现网络功率损失的降低.优化过程中，所施加的约束条件有节点的电压、分支的电流和网络辐射状态.电容器优化配置可控制无功功率，进而降低配电线路的功率损耗.文中提出改进的二进制粒子群优化算法(IBPSO)，并在16节点系统上进行测试，测试结果表明，同时解决重构和电容配置这两个问题比单独解决的优化效果要好.仿真和对比分析表明，网络重构和电容器配置的同步实施可获得最佳的网络状态.根据功率损失的减少量，优化方案实施的优先顺序如下:①同时重构网络和配置电容器;② 先进行网络重构，然后配置电容器;③ 先放置电容器，然后进行网络重构.文中建立的数学模型是以配网损耗作为目标函数，下一步将开展节点增加、负荷增长、配网扩展等要素对配网重构影响的研究.

References)

［1］江亚群，陈祝峰，黄 纯，等.基于启发式规则与和声搜索的配电网重构算法［J］.湖南大学学报:自然科学版，2014，4(3):61-67.

Jiang Yaqun，Chen Zhufeng，Huang Chun，et al.Distribution network reconfiguration based on heuristic rules and harmony search algorithm［J］.Journal of Hunan University:Natural Sciences，2014，4(3):61-67.(in Chinese)

［2］汲国强，吴文传，张伯明，等.以降损和载荷均衡为目标的地区电网网络重构快速算法［J］.电网技术，2012，36(11):172-178.

Ji Guoqiang，Wu Wenchuan，Zhang Boming，et al.Regional network reconfiguration algorithm for loss reduction and loading equilibrium［J］.Power System Technology，2012，36(11):172-178.(in Chinese)

［3］Ahmadi H，José R Martí.Mathematical representation of radiality constraint in distribution system reconfiguration problem［J］.International Journal of Electrical Power＆Energy Systems，2015，64:293-299.

［4］刘志勇，刘杨华，林舜江，等.基于模糊多目标协调优化的配电网络重构研究［J］.电力系统保护与控制，2014，42(4):133-138.

Liu Zhiyong，Liu Yanghua，Lin Shunjiang，et al.Fuzzy multi-objective coordination optimization for distribution network reconfiguration［J］.Power System Protection and Control，2014，42(4):133-138.(in Chinese)

［5］戴志辉，崇志强，焦彦军，等.含分布式电源的配电网多目标供电恢复［J］.电网技术，2014，38(7):1959-1965.

Dai Zhihui，Chong Zhiqiang，Jiao Yanjun，et al.Multiobjective service restoration of distribution network containing distributed generation［J］.Power System Technology，2014，38(7):1959-1965.(in Chinese)

［6］李秀卿，李 文，杨云鹏，等.含有风力发电机组配电网多目标重构的研究［J］.电力系统保护与控制，2012，40(8):57-62.

Li Xiuqing，Li Wen，Yang Yunpeng，et al.Distribution network multi-objective reconfiguration with wind turbines［J］.Power System Protection and Control，2012，40(8):57-62.(in Chinese)

［7］Sathish Kumar K，Naveen S.Power system reconfiguration and loss minimization for a distribution systems using“Catfish PSO”algorithm［J］.Frontiers in Energy，2014，8(4):434-442.

［8］韩 飞，杨春生，刘 清.一种改进的基于梯度搜索的粒子群优化算法［J］.南京大学学报:自然科学版，2013，49(2):196-201.

Han Fei，Yang Chunsheng，Liu Qing.An improved particle swarm optimization based on gradient search［J］.Journal of Nanjing University:Natural Science，2013，49(2):196-201.(in Chinese)

［9］Veera Venkata Satya Naryana Murty，Ashwani Kumar.Comparison of optimal capacitor placement methods in radial distribution system with load growth and ZIP load model［J］.Frontiers in Energy，2013，7(2):197-213.

［10］Samimi Asl T，Jamali S.Optimal capacitor placement size and location of shunt capacitor for reduction of losses on distribution feeders［C］∥International Conference on Clean Electrical Power，2009:223-226.

［11］Mwakabuta N，Sekar A.Study of the application of evolutionary algorithms for the solution of capacitor deployment problem in distribution systems［C］∥40thSoutheastern Symposium on System Theory，2008:178-182.

［12］Mohamed Imran A，Kowsalya M.Optimal distributed generation and capacitor placement in power distribution networks for power loss minimization［C］∥International Conference on Advances in Electrical Engineering，2014:1-6.

［13］Gallano R J C，Nerves A C.Multi-objective optimization of distribution network reconfiguration with capacitor and distributed generator placement［C］∥Tencon IEEE Region10Conference，2014:1-6.

［14］Farahani V，Sadeghi S H H，Askarian H，et al.Maximum loss reduction by an improved reconfiguration method and capacitor placement［J］.IEEE International Conference on Power＆Energy，2010:270-275.

［15］Rani D S，Subrahmanyam N，Sydulu M.Self adaptive harmony search algorithm for optimal capacitor placement on radial distribution systems［C］∥International Conference on Energy Efficient Technologies for Sustainability，2013:1330-1335.

［16］Sirjani R，Mohamed A，Shareef H.Heuristic optimization techniques to determine optimal capacitor placement and sizing in radial distribution networks:a comprehensive review［J］.Przeglad Elektrotechniczny，2012，7(A):1-7.

［17］Deese A S.Comparative study of accuracy and computation time for optimal network reconfiguration techniques via simulation［J］.International Journal of Electrical Power＆Energy Systems，2014，63(12):394-400.

［18］Araujo L R D，Penido D R R，Júnior S C，et al.Comparisonsbetween the three-phase currentinjection method and the forward/backWard sweep method［J］.International Journal of Electrical Power＆Energy Systems，2010，32(7):825-833.

［19］Chih M.Self-adaptive check and repair operator-based particle swarm optimization for the multidimensional knapsack problem［J］.Applied Soft Computing，2015，26(1):378-389.

［20］焦 鹏，王新政，徐衡博.基于IBPSO的模拟电路故障特征提取方法［J］.兵工自动化，2013，32(6):66-69.

Jiao Peng，Wang Xinzheng，Xu Hengbo.Fault feature extraction method of analog circuits based on IBPSO［J］.Ordnance Industry Automation，2013，32(6):66-69.(in Chinese)

［21］汪 超，马红卫，胡志坚，等.基于蚁群系统(ACS)的配电网重构［J］.继电器，2006，34(23):35-38.

Wang Chao，Ma Hongwei，Hu Zhijian，el al.Distribution network reconfiguration based on ant colony system［J］.Relay，2006，34(23):35-38.(in Chinese)

［22］Keshavarz M，Ranjbar A M，Sedighizadeh M，et al.Biobjective function micro grid optimal operation using a hybrid algorithm［J］.International Journal on Technical and Physical Problems of Engineering，2013，14(5):149-162.