八自由度人-车-路耦合模型振动分析

孙阳敏，时培成

安徽工程大学机械与汽车工程学院，安徽芜湖，241000



八自由度人-车-路耦合模型振动分析

孙阳敏，时培成

安徽工程大学机械与汽车工程学院，安徽芜湖，241000

过于复杂的多自由度汽车振动模型难以计算分析，为了获得尽量简化且保证一定精确度的模型，建立了八自由度人-车-路耦合振动模型，推导出振动微分方程，并运用SIMULINK软件将所建立的八自由度数学模型转化为仿真模型。通过运动仿真，得到车身及人-座椅系统的振动加速度、悬架动挠度和车轮动位移等响应曲线。经对所得图形数据的比较分析，选择的车型参数匹配是合理的。建立的汽车振动模型及其仿真程序和计算过程对研究车辆行驶的平顺性、对简化汽车振动系统模型有一定的参考价值。

八自由度振动模型；随机振动；耦合振动；乘坐舒适性

文献[1]建立车路耦合系统的分析模型及其动力平衡方程，对车辆运动初速度、加速度以及路面不平顺对车体振动影响进行了分析。文献[2]运用ADAMS/View和LifeMOD软件构建了人-车系统生物力学仿真模型，重点研究人体乘坐的舒适性。文献[3]采用五自由度振动模型，考虑车路耦合，用传递矩阵法进行了人-车-路相互作用分析，考虑了不同路面类型和行车速度的影响。这些研究未将车身和人-座椅系统综合考虑，也未对二者之间的关系作比较分析。鉴于以上两点，本文将对八自由度人-车-路耦合振动模型进行平顺性仿真分析，建立人-车-路八自由度模型的振动微分方程，运用SIMULINK软件将所建立的八自由度数学模型转化为仿真模型，使建立的模型模块化、参数化。

1 八自由度振动模型及其振动微分方程的建立

1.1 八自由度耦合振动模型

本文建立八自由度汽车模型[4]时作如下假设：(1)汽车以匀速直线运动行驶；(2)车身部分的质量和刚度远大于悬架，且其固有频率也远高于激励频率，故可将车身部分简化为刚体，并忽略悬架的质量；(3)车体在平衡位置附近微幅振动；(4)悬架、轮胎简化为仅考虑刚度和阻尼的元件；(5)车身质量由车身、前悬挂质量、后悬挂质量组成。将车身部分简化为受到四个激励源的具有横向、纵向、垂向的八自由度振动系统。

1.2 八自由度振动模型的振动微分方程

根据图1，利用牛顿法，可得到八自由度振动模型的振动微分方程式为：

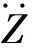
(1)

其中，质量矩阵：M=[m1m2m3m4m5mIxIy]；

其中，k66=-k1-k2-k3-k4-k5；

k67=k1l5-k2l6-k3l6+k4l5+k5l1；

k68=-k1l3-k2l3+l4k3+k4l4-k5l7；

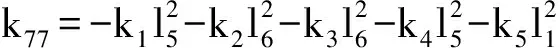
k78=k1l3l5-k2l6l3+k3l6l4-k4l5l4+k5l7l1；

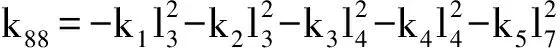
k76=k67；k86=k68；k87=k78

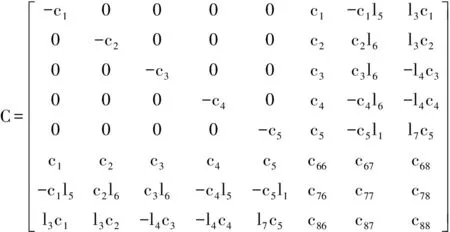
其中，

c66=-c1-c2-c3-c4-c5；

c67=c1l5-c2l6-c3l6+c4l5+c5l1；

c68=-c1l3-c2l3+l4c3+c4l4-c5l7；

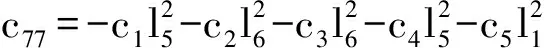
c78=c1l3l5-c2l6l3+c3l6l4-c4l5l4+c5l7l1；

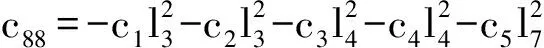
c76=c67；c86=c68；c87=c78。

Z=(z1z2z3z4z5z θ φ)T；

Q=(qflqrlqrrqfr)T。

2 路面模型的建立

2.1 时间频率功率谱描述

基于功率谱函数,依据不同理论,可以有白噪声法[5-6]、谐波叠加法[7-8]、PSD离散采样法[9]、AR/ARMA法[10]等多种路面不平度随机激励单点(轮胎)时域模型。路面输入模型能否准确地反映实际研究路面的特征，对分析研究的准确性有决定性的影响。

2.2 路面模型的建立

选择B级路面作为测试路面，汽车行驶速度为20m/s，前后轮的路面谱输入时间间隔t=L/v=0.138s，则可在SIMULINK中建立前后轮的路面谱仿真模型和仿真输入函数，如图1、图2所示。为便于接下来的耦合系统仿真，再利用SIMULINK中的SUBSYSTEMCREATER分别将前后轮的路面函数创建成子系统。

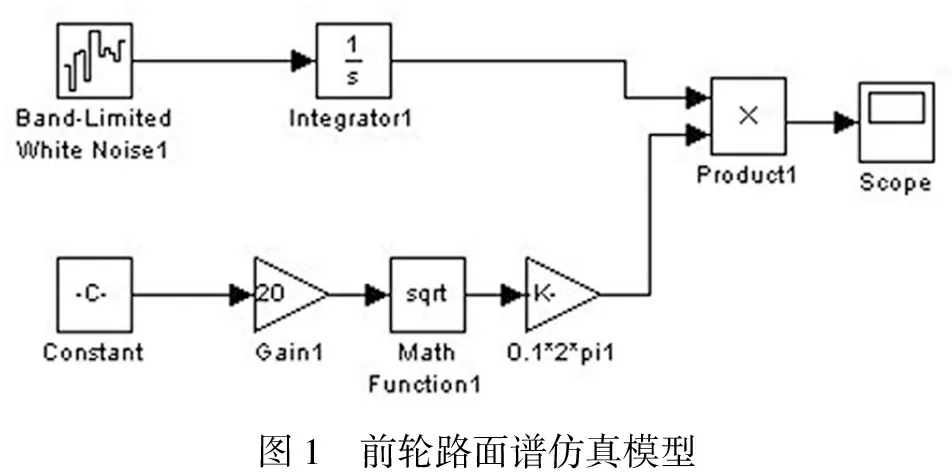
图1 前轮路面谱仿真模型

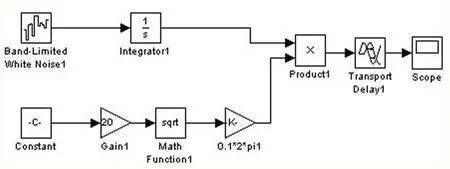
图2 后轮路面谱仿真模型

3 SIMULINK建立八自由度汽车模型

在SIMULINK中建立八自由度车辆振动仿真模型[11]。编程中运用的数据见表1，在输入四个车轮的路面谱时考虑了四轮之间的互谱。

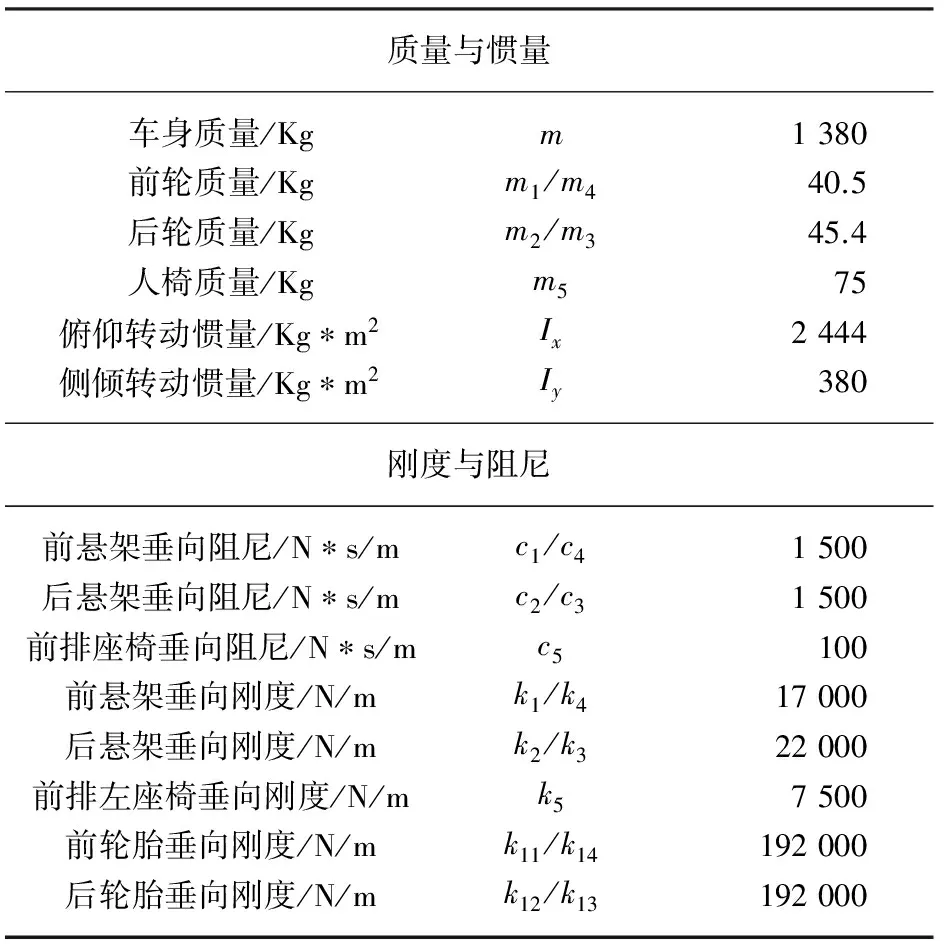
表1 整车车辆模型参数

(续表)

4 八自由度耦合模型的平顺性仿真与分析

4.1 八自由度仿真位移曲线

选定B级路面为测试路面，车速为20 m/s时的仿真曲线如图3至图10。

从图3至图10可看出，四个车轮的位移，两后轮比两前轮有时间延迟，但由于延迟时间极小，所以在图上表现不是很明显。另外，车身位移与人椅系统的位移曲线走势是一致的，人椅系统的位移幅度和车身的位移幅度稍有增大，但由于刚度和阻尼的缓冲，故其振动幅度都不大。俯仰角变化和侧倾角的变化值都是非常小的一个数值，可忽略不计。

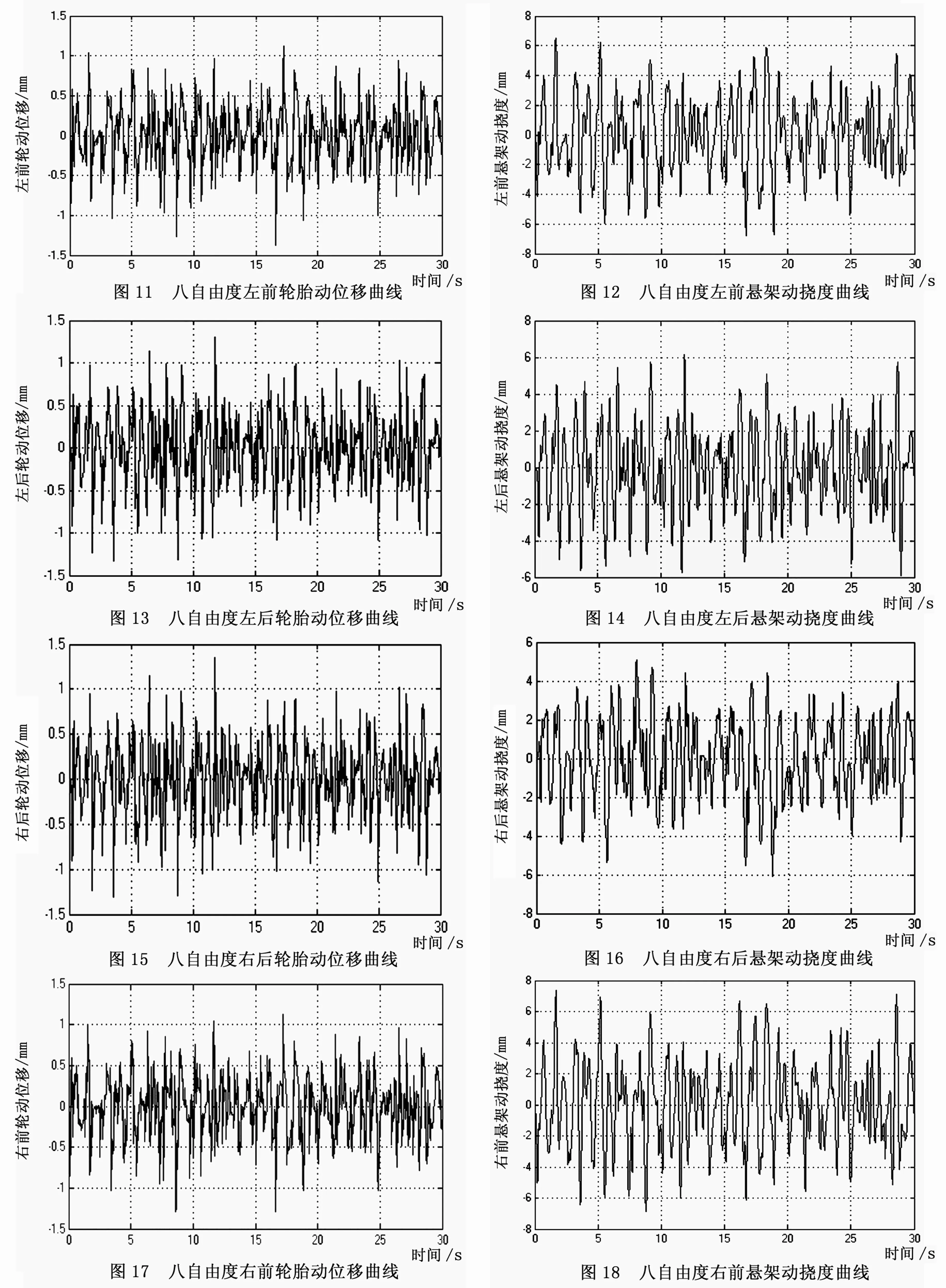
4.2 八自由度仿真悬架动挠度和轮胎动位移曲线

路面采用B级路面输入，采用u=20 m/s进行仿真，仿真结果如图11至图18所示。

由图11至图18可看出，八自由度模型在B级路面，20m/s的车速下，八自由度模型的动挠度数值都不大，在合理的数值范围内，八自由度模型的行驶比较平稳；八自由度模型的前后轮的动位移数值都不大，对汽车操纵稳定性并没有太大的影响。

4.3 八自由度仿真加速度曲线

在B级路面，在20 m/s车速下，车身和人椅系统的加速度数值也不相同，仿真图形图19和20，并据此判断乘客的舒适程度，由此对行车舒适性进行评价。

在B级路面下，汽车在20 m/s的行驶状态下，八自由度模型的乘坐状态较为舒适，说明汽车的参数选择合理，建立的模型具有一定实用价值。

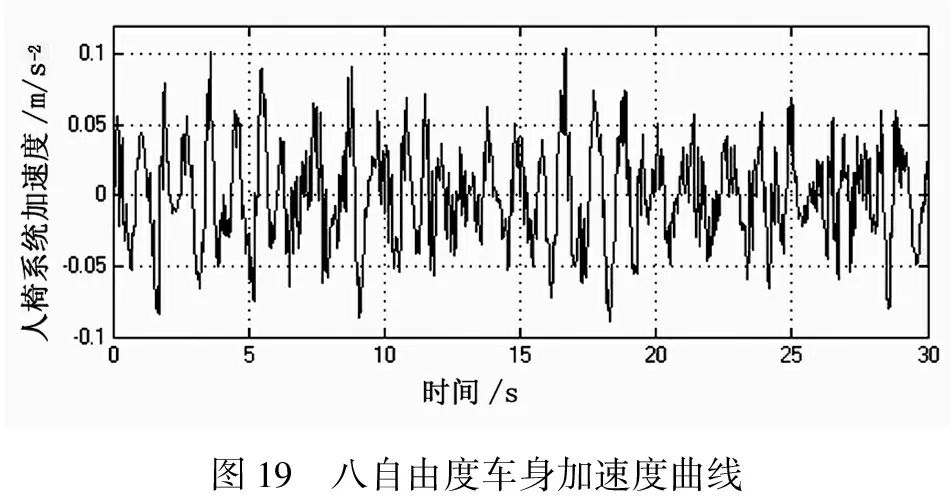
图19 八自由度车身加速度曲线

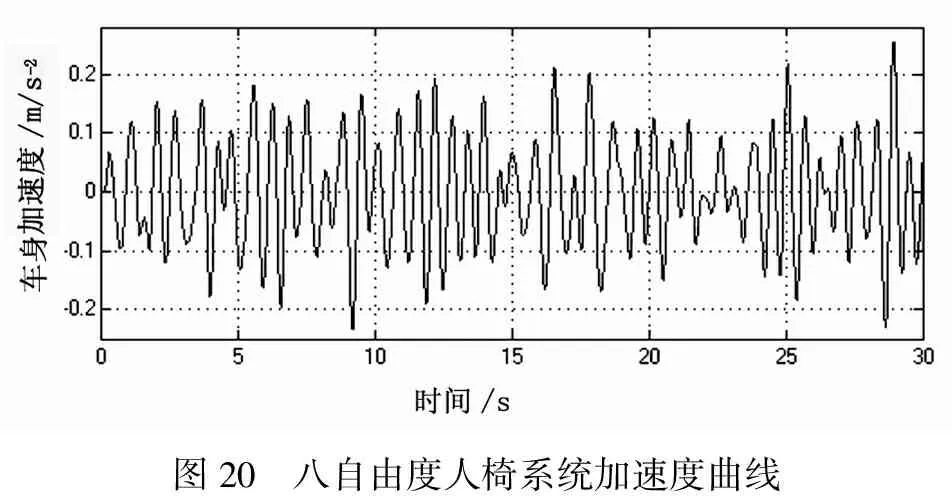
图20 八自由度人椅系统加速度曲线

5 结束语

本文以整车模型为研究对象，集中讨论了行使车速对汽车平顺性的影响，为此建立了道路仿真模型，让其在常规速度下直线行使，比较其平顺性指标。经比较分析，车身的振动大于人椅系统振动，但二者特性参数较为相似，均在合理数值范围。仿真结果表明，所选择车型的参数匹配是合理的，为简化汽车振动系统模型，进一步探索利用现有软件进行仿真分析，解决汽车振动带来的汽车操作稳定性、平顺性和安全性等问题提供参考。

[1]张丙强,李亮.车辆—路面耦合振动系统模型与仿真分析[J].振动与冲击,2010,29(2):35-38

[2]张鄂,刘中华,计志红,等.人-车系统的人体乘坐舒适性仿真及实验研究[J].工程设计学报,2010(2):107-113

[3]张洪亮,杨万桥.基于人-车-路五自由度振动模型的路面平整度评价方法[J].交通运输工程学报,2010(4):16-22

[4]余志生.汽车理论[M].3版.北京：机械工业出版社，2000：1-201

[5]ZHANG Yonglin,ZHANG Jiafan.Numerical simu-lation of stochastic road process using white noise fil-tration[J].Mechanical Systems and Signal Process-ing,2006,20(2):363-372

[6]Yoshimura A.Semi-active suspension of passen-ger cars using fussy reasoning and the field testing[J].Int J of Vehicle Designs,1998,19(2):150-166

[7]张永林.用谐波叠加法重构随机道路不平顺高程的时域模型[J].农业工程学报,2003,19(6):32-35

[8]郑军,钟志华.非线性汽车行驶平顺性模型的神经网络优化[J].汽车工程, 2001, 23(3):172-176

[9]张永林,胡志刚,陈立平.时空相关车辆道路的高效数值仿真[J].农业机械学报,2005,36(9):13-24

[10]张永林,李诗龙,杨建林.汽车道路随机不平顺的时序模型重构[J].武汉理工大学学报:交通科学与工程版.2005,29(6):883-886

[11]姜鹏.汽车悬架系统的仿真分析与参数优化设计[D].杭州：浙江大学研究生院,2006：3-55

(责任编辑：汪材印)

The Vibration Analysis of Eight Degrees of Freedom Man-vehicle-road Coupled Model

SUN Yangmin，SHI Peicheng

School of Mechanical and Automotive Engineering, Anhui Polytechnic University,Wuhu Anhui,241000,China

It is difficult to calculate and analyze a complicated automobile vibration model of multiple-degree-of-freedom. To obtain a simplified and relatively accurate model, the 8-DOF man-vehicle-road coupled vibration model was established and the vibration differential equation was derived. The 8-DOF mathematical model was translated into a simulation model by using Simulink. The response curves of the vibration acceleration, suspension dynamic deflection and wheel dynamic displacement of the bodywork and man-chair system were gotten from the movement simulation. The comparison and analysis of the figures and data reveal that the parameters matching of the selected model is reasonable. The automobile vibration model and it's simulation program and computation process have some reference value to study the ride comfort and to simplify the automotive vibration system.

8-DOF vibration model;random vibration;coupled vibration; ride comfort

10.3969/j.issn.1673-2006.2015.03.025

2014-11-30

安徽省教育厅自然科学研究一般项目“电动汽车驱动系统硬件在环仿真研究”(KJ2012B027)。

孙阳敏(1989-)，安徽宣城人，硕士生，主要研究方向：汽车理论与应用工程。

U461

A

1673-2006(2015)03-0093-05