运用数值微分方法研究核脉冲信号放大电路

周 伟, 周建斌, 肖永江, 周 靖, 赵 祥

(1.成都理工大学 核技术学院，四川 成都 610059; 2.萍乡学院 机电系，江西 萍乡 337055)



运用数值微分方法研究核脉冲信号放大电路

周 伟1, 周建斌1, 肖永江2, 周 靖1, 赵 祥1

(1.成都理工大学 核技术学院，四川 成都 610059; 2.萍乡学院 机电系，江西 萍乡 337055)

提出了一种崭新的基于数值微分法的时域内核脉冲信号放大电路的分析方法，弥补了频域分析方法在脉冲信号的宽度、形状和幅度特性分析上的不足。从实际信号放大电路出发，运用基尔霍夫电流定律，建立输入信号和输出信号之间的一阶微分方程关系等式。方程解算过程中，利用数值微分算法求解，获得输入输出之间的数学关系模型。通过反相放大电路和同相放大电路等实际电路的测试结果，表明时域内运用数值微分算法研究核脉冲信号放大电路的方法是可行的。

信号放大电路； 数值微分法； 时域分析； VBA仿真

0 引 言

信号放大电路作为一种常用信号处理电路，在仪器仪表设计领域中得到了广泛的应用。放大电路常以运算放大器为基础，通过将运算放大器、电阻和电容等进行组合，并引入反馈，组成如反相放大电路、同相放大电路等常用电路形式，以实现对核信号的放大、滤波以及成形等功能。核辐射测量中，放大器有两种形式，一是前置放大器，二是主放大器[1-2]。前置放大器需要尽可能地靠近前级探测器，以减少探测器输出端到放大器输入端之间分布电容的影响，提高信噪比以及减少外界干扰[3]。主放大器用于将前置放大器的输出信号作进一步放大和成形，同时保持探测器输出的有用信息，如射线的能量信息和时间信息等，尽可能减少它们的失真[4-5]。

在信号放大电路的设计与分析上，传统的方法有两种。一种是运用纯数学变换(拉氏变换、傅里叶变换等)的方式，将对信号的分析由时域转换到频域进行[5～7]，另一种是基于电路仿真软件(Multisim，Pspice等)直接进行频率响应和基本性能分析[8～13]。上述两种方法都忽略了信号放大电路在时域内的特性，例如核脉冲信号的随机性、宽度、幅度和形状等。论文从核脉冲信号放大电路分析入手，基于基尔霍夫电流定律(Kirchhoff Current Law，KCL)构建输入与输出之间一阶微分方程关系等式，再运用数值微分法求解该等式[14-15]，最后得到时域内信号放大电路的数学模型。同时，论文也对建立的数学模型进行了仿真验证。

1 反相放大电路数学模型

图1是一个典型的反相放大电路，常用于核脉冲信号的前置放大器和主放大器中。

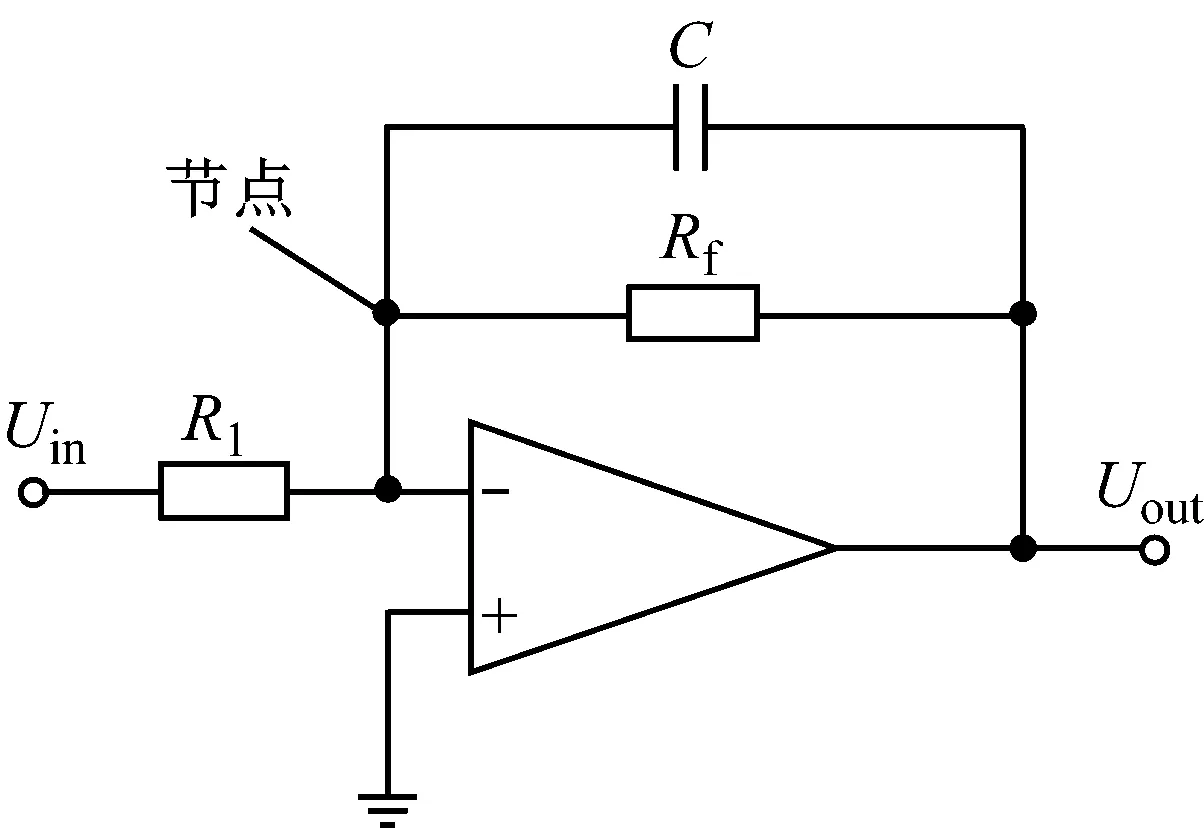
图1 反相放大电路

上述电路中，运用KCL以所标位置为“节点”，可以建立输入信号Uin和输出信号Uout之间的关系等式，

(1)

式中，Un和Up分别是运算放大器的负端和正端电压。根据运算放大器“虚短”特性可知，Un=Up=0，则式⑴可以变换为,

(2)

从形式上可知，式(2)是一个一阶微分方程。由于核脉冲信号具有统计涨落的特性，对于式(2)，采用求解连续函数微分方程解的方法是不合适的。为了能够在时域里面对式(2)进行求解，将输入、输出的模拟信号转换成具有一定时间间隔(由ADC采样频率决定)的离散序列，即令Uin=x[n]，Uout=y[n]，dt=Δt。其中，Δt为ADC采样间隔，则式⑵可以表示为：

(3)

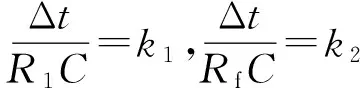
(4)

由此可见，式⑷即为图1反相放大电路的数学模型。输出信号的脉冲宽度、形状和幅度随着参数k1和k2的变化而变化。实际应用过程中，ADC选定后，Δt也随之被确定，k1和k2只与电路中的电阻R1、Rf和电容C有关。此时，调整电阻和电容的值，可以得到不同的输出信号，从而也实现时域内对该放大电路的分析。1.2 数学模型的仿真

基于VBA平台完成了反相放大电路数学模型的仿真测试。其中，VBA技术(Visual Basic for Application)是微软公司为工程应用而专门设计的一种可视化程序开发环境。将VBA技术和Excel应用相结合，不仅能够使用Excel提供的库函数，访问其特有的命令和结构，使用统计分析和图表绘制等功能；还可以创建自定义的用户界面[16-17]。实际仿真过程中，选择叠加噪声的标准负指数信号作为输入信号，可表示为：

沥青性能优劣直接影响到排水沥青混凝土路用性能及耐久性。本研究选用A型和B型国产沥青改性剂TAFPACK—Seper（简称TPS），改性基质沥青来制备高黏度改性沥青，并参照《公路工程沥青及沥青混合料试验规程》进行相应试验，主要技术性能检测结果见表1。

(5)

其中：A表示标准负指数信号的幅度；τ表示时间常数；B(0.5-Rnd(1))表示叠加的噪声。仿真时，为了观察数学模型的信号放大和滤波等综合处理性能，选择的4组输入信号在信号幅度和叠加噪声上是不同的。其中，x1[n]为单一噪声信号。

(6)

图2是不同k1，k2参数反相放大电路数学模型的仿真波形。其中，取Δt=50 ns，对于输出信号Output1，k1=k2=0.5，可以选择R1=Rf=100 Ω，C=1 nF的电阻和电容组合。

图2 不同参数时反相放大电路数学模型的仿真波形

从图2中可以看出，在输出信号的幅度上，根据电阻R1和Rf的组合进行控制。另外，在输出信号的信噪比上，电容C起到低通滤波器的作用。综合选择滤波器的参数(Rf和C)，可以控制输出信号的脉冲宽度和形状。

2 同相放大电路数学模型

2.1 数学模型的建立

图3是一种常见的同相放大电路。

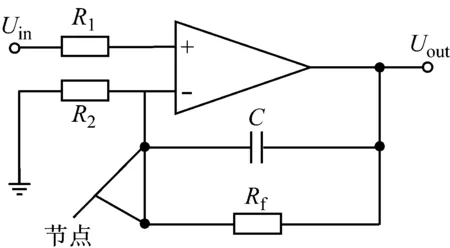
图3 同相放大电路

采用相同的分析方法，输入信号Uin和输出信号Uout之间的关系等式可以描述为：

(7)

其中，Un=Up=Uin，则式(7)可以转换为：

(8)

令Uin=x[n]，Uout=y[n]，dt=Δt，式(8)经过变换后，得到：

(8)

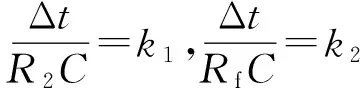
(9)

2.2 数学模型的仿真

图4是不同k1，k2参数同相放大电路数学模型的仿真波形。其中，取Δt=50 ns，对于输出信号Output1，k1=0.4，k2=0.2，可以选择R2=125 Ω，Rf=250 Ω，C=1 nF的电阻和电容组合。

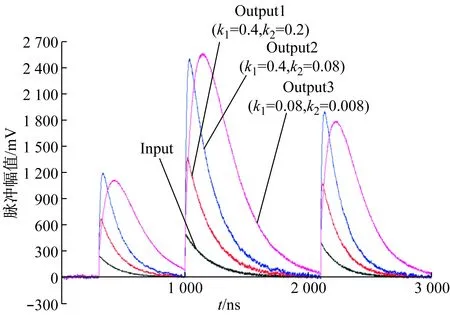
图4 不同参数时反相放大电路数学模型的仿真波形

3 结 语

在时域内引入数值微分法研究核脉冲信号放大电路的数学模型是一次成功的尝试。时域内实现信号的宽度、形状和幅度等特性分析，这是对频域分析方法是极大的补充。论文中，先后研究了反相放大电路和同相放大电路实际电路的数学模型，并完成了标准负指数信号(叠加噪声信号)的仿真测试。测试结果显示所研究数字成形模型的正确性。可以预见，随着实时高速采样技术的快速发展，采样的最小时间单元可以微分到Psec量级(部分可以达到fsec量级)，从而更加缩小离散系统与连续系统的时间界限。鉴于在时间域内的模型简单、概念清楚、易于实现、对比直观等优点，数值微分法对于完善离散系统的时域分析方法必将会有极大的促进。此外，研究的顺利开展也得益于VBA软件仿真平台便捷的完成了数学模型的仿真验证。最后，在前期工作基础之上，下一步的研究包括2个方面：① 完成实际核脉冲信号测试，并进一步完善优化数学模型。进而探讨数学模型基于硬件载体(FPGA或DSP器件)的实现技术，以提升实际工程应用中核仪器系统的综合性能;② 继续运用数值微分法研究滤波电路、成形电路等实际信号处理电路的时域内数学模型，从而为研究电子电路仿真软件的开发工作提出一些新的思路。

[1] 王经瑾, 范天民, 钱永庚. 核电子学[M]. 北京：原子能出版社, 1983.

[2] 王芝英, 楼滨乔, 朱俊杰, 等. 核电子技术原理[M]. 北京：原子能出版社, 1989.

[3] 薛 楠. Protel DXP 2004 原理图与PCB设计实用教程[M]. 北京：机械工业出版社, 2012.

[4] 汤 彬, 葛良全, 方 方, 等. 核辐射测量原理[M]. 哈尔滨：哈尔滨工程大学出版社, 2011.

[5] 薛 山. MATLAB基础教程[M]. 北京：清华大学出版社, 2011.

[6] 刘 维. 精通Matlab与C/C++混合程序设计(第3版)[M]. 北京：北京航空航天大学出版社, 2012.

[7] 黄 喜, 张新亮, 董建绩, 等. 半导体光放大器超快折射率变化动态特性的研究[J]. 物理学报，2009,58(5):3185-3192.

[8] 朱高中. 基于Multisim的高频谐振功率放大器仿真实验[J]. 实验室研究与探索，2013,32(2):92-94.

[9] 郑 鑫, 张晓洁. 虚拟实验室立体化教学资源平台建设简[J]. 实验室研究与探索，2014,33(8):109-111.

[10] 蒲永红, 余 粟, 王维荣. Multisim辅助电工电子实验教学的探讨[J]. 实验室研究与探索，2013,32(9): 174-177.

[11] 刘丽娜, 杜钦君. OrCAD PSpice在自动化专业综合设计型实验课程中的应用探索[J]. 实验技术与管理，2013,30(11):133-136.

[12] 王连英. 基于Multisim10的电子仿真试验与设计[M]. 北京：北京邮电大学出版社, 2013.

[13] 周润景. 基于PROTEUS的电路及单片机设计与仿真[M].第2版. 北京：北京航空航天学出版社, 2010.

[14] Zhou J B, Zhou W, Lei J R,etal. Study of time-domain digital pulse shaping algorithms for nuclear signals[J]. Nuclear Science & Techniques, 2012, 23(3):150-155.

[15] Zhou J B, Hong X, Wang R B,etal. Study of recursive model for pole-zero cancellation circuit[J]. Nuclear Science & Techniques, 2014(010403).

[16] 谭浩强. Visual Basic程序设计[M].第3版 北京：清华大学出版社, 2012.

[17] 谭浩强. QBasic语言教程[M].第2版. 北京：电子工业出版社, 2002.

Study of Nuclear Signal Amplifier Circuit Based on Numerical Differential Method

ZHOUWei1,ZHOUJian-bin1,XIAOYong-jiang2,ZHOUJing1,ZHAOXiang1

(1. Institute of Nuclear, Chengdu University of Technology, Chengdu 610059, China;2. School of Mechanical and Electronic Engineering, PingXiang Institute, Pingxiang 337055, China)

In the time-domain, a novel method of nuclear pulse signal amplifier circuit is presented based on numerical differential in this paper. The method can cover the many shortages of the analyzing methods in the frequency-domain, such as pulse width, shape and amplitude. According to the Kirchhoff's current law, an equation between input and output is established based on actual signal amplifier circuits. And after equation is solved, the mathematical model can also be acquired by using numerical differential. The simulating results of the inverting amplifying circuit and non-inverting amplifier circuit for nuclear pulse signal show that it is feasible for studying the amplifier circuits by using numerical differential method in the time-domain.

signal amplifier circuit; numerical differential method; time-domain analysis; simulation based on VBA

2014-08-11

周 伟(1979-)，男，江苏南京人，博士，副教授，系主任，从事核信号获取与数字处理的研究工作。

Tel.:13551805424,02884078773;E-mail:zhouwei@cdut.edu.cn。

TL 821

A

1006-7167(2015)03-0134-03