基于序关系和冲量模型的航空装备安全性模型

邢乃若， 惠晓滨， 孟祥飞

(空军工程大学 装备管理与安全工程学院，陕西 西安 710051)



基于序关系和冲量模型的航空装备安全性模型

邢乃若， 惠晓滨， 孟祥飞

(空军工程大学 装备管理与安全工程学院，陕西 西安 710051)

针对航空装备安全性分析的复杂问题，建立了描述航空装备安全性的分析模型。通过对能量意外释放论、轨迹交叉论和管理失误论的分析，得出了影响航空装备安全性的主要因素。在此基础上，利用系统耦合理论、序关系分析法和冲量过程模型建立了描述航空装备安全性的数学模型。通过对模型和案例的分析，得出了航空装备安全性与可靠性之间的关系以及提高航空装备安全性的措施。

航空装备安全性； 影响因素； 系统耦合理论； 序关系分析法； 冲量过程模型

0 引 言

虽然航空事故尤其是重大安全性事故发生概率很小，但每年发生空难的次数和一次空难所造成死亡人数多则上百人少则十数人的残酷事实却让社会难以接受。安全是各类航空装备设计、研制、生产、使用和维修保障的首要要求，是装备在规定的或非规定的条件下，都能保持稳定、完整、有序的可控状态的程度[1]，是人们始终关注的焦点。目前，我国航空领域主要使用的分析法有故障模式影响及危害性分析(FMECA)、事件树分析(ETA)、事故树分析(FTA)、预先危险性分析(PHA)、危险和可操作性研究(HAZOP)和事故因果分析(CCA)等。但这些方法或主观性太强、或适用范围受限，难以从定量和定性结合的角度分析问题。因此，本文在充分考虑影响航空装备安全的主要因素的基础上建立安全度函数来刻画航空装备的安全性。

1 装备安全性内涵

由于研究目的、研究内容和研究方式的差异，不同的国家或研究机构对安全性的定义也不同，目前普遍被人们接受的定义主要有以下几个[2]。

(1) GJB451A-2005中规定：安全性是指产品所具有的不导致人员伤亡、系统毁坏、重大财产损失或不危及人员健康和环境的能力。

(2) GB/T3187-1994中规定：安全性是在设计时为使产品失效而不致引起人身物质等重大损失采取的预防措施。

(3) MIL-STD-882C中规定：安全性是在系统寿命周期的所有阶段，以使用效能、时间、费用为约束条件，应用工程和管理的原理、规则和技术，使系统获得最佳安全性。

以上是从不同的角度对安全性进行定义，在本文中采取第一种定义。用安全度来描述航空装备安全性的高低，航空装备的安全度是指航空装备在规定的时间内，在规定或非规定的条件下不导致人员伤亡、毁坏系统、重大财产损失或不危及人员健康和环境的概率，它是反映航空装备安全影响因素以及因素之间关系的函数式，用S(t)来表示[3]。和装备的可靠度一样，安全度也是一个关于时间t的函数，取值范围为[0,1]。可靠性是安全性的基础，没有可靠性，谈安全性就没有意义；但提高可靠性只能在一定程度上提高安全性，超过一定程度，再提高可靠性对提高航空装备的安全性并没有多少意义，而且会导致大量资源的浪费[4]。

2 影响航空装备安全性的因素

1961年，吉布森提出了解释事故发生的物理本质的能量意外释放论。他认为，事故是一种不正常或不希望的能量释放，各种形式的能量是构成伤害的直接原因，1966年哈登对此进行了完善[5]。航空装备尤其是在高空高速飞行的飞机具有非常大的能量，一旦发生能量的意外释放很可能会造成严重事故。此外，当外界环境的能量和飞机能量交互发生问题，外界环境能量作用于飞机并且超过了飞机的防护极限时同样会造成严重事故，如飞机遭到雷击或者鸟撞飞机。所以外界环境在一定程度上影响着航空装备的安全性。

轨迹交叉论认为：在事故发展的进程中，人的因素和物的因素在事故致因中占有同样重要的地位。人的因素运动轨迹与物的因素运动轨迹的交点就是事故发生的时空，即人的不安全行为和物的不安全状态发生于同一时空或者说人的不安全行为与物的不安全状态相遇时，将在此时空点发生事故。按照该理论，可以通过避免人与物的两种运动轨迹交叉，即避免人的不安全行为和物的不安全状态同时空出现来预防事故的发生[6]。由于该理论提出较早，具有一定的局限性。对于现代化设备，尤其是航空装备即使人的不安全行为与物的不安全状态没有交叉，单一一种原因仍然可能造成严重的后果。

管理失误论者认为：如果管理者能够充分发挥管理职能，就可以有效地控制人的不安全行为和物的不安全状态，从而避免事故的发生[7]。虽然该理论没有揭示管理失误的形成机制及导致个体失误的作用机制，但说明了一个事实：管理因素是事故的一个贡献因素。

所以在考虑影响航空装备使用安全的因素时，主要考虑人的可靠性、装备的可靠性、环境的适应性和管理的科学性四个方面。

3 航空装备安全性建模

影响航空装备安全的四个因素中任何一个发生问题都可能造成航空装备的安全性事故，因此，在一定的程度上可以将四个因素之间的关系抽象为串联关系。各影响因素之间的交互(耦合)冲突同样会造成航空装备的不安全状态，环境因素与其他因素交互最多并且最易发生变化。因此，在航空装备安全性建模时必须充分考虑上述关系。

取系统的安全度为S(t)；人的可靠度为R1；装备的可靠度为R2；环境的适应可靠度为R3；管理的科学可靠度为R4。航空装备安全性建模的步骤如下所述。

3.1 影响因素定量化

(1) 人的可靠度。人的可靠度定义为在系统工作的任何阶段上，操作者在规定的时间内成功地完成规定操作的概率。这里所说的成功的完成操作，并不是在操作中毫无错误，而是允许有错误，但它对成功的完成操作并不发生重大影响[8]。

(2) 装备的可靠度。装备的可靠性用装备的使用可靠度进行度量，即产品在规定的任务剖面内完成规定功能的概率[9]。任务可靠度仅考虑完成任务失败的故障影响，即只统计任务期间危及任务成功的故障。

(3) 环境的适应可靠度。环境的适应度定义为在规定的时间内外界环境能够保证航空装备完成规定功能的概率。在规定的时间内将任务剖面内规定的环境中最适宜执行任务的环境的适应可靠度定为1，环境越恶劣越不适宜执行任务，则环境的适应可靠度量值越小。所有环境的适应可靠度量值在[0,1]内变化。

(4) 管理的科学可靠度。管理的科学可靠度定义为在规定的时间内管理措施能够保证航空装备完成规定功能的概率。可以请专家在某个时间段内对对象单位的安全文化建设、安全制度贯彻、安全教育落实、安全能力培训、安全决策失误率、事故率、损失率七个方面进行考察，然后在[0,1]内打分。其中1表示管理科学可靠度最高;0表示管理科学可靠度最低。

3.2 计算各影响因素之间的影响度

各因素之间的往往具有紧密的联系，一个因素的改变很可能会对其他因素产生不同程度的影响。如恶劣的环境变化会使人员的心理产生紧张，进而影响到人的可靠度，同样恶劣的环境也可能降低航空装备的可靠度。由于因素之间作用的机理相当复杂，在此只研究因素之间相互作用的宏观层面，并不讨论相互作用的机理。

用aij表示因素i对因素j的影响程度，即因素i的可靠度变化一个单位，因素j的可靠度变化aij个单位。通过数据分析，可建立两个因素之间的一元线性回归模型或一元非线性回归模型。在一元线性回归模型中取自变量前的系数作为aij；对于可线性化一元非线性回归模型可先将其线性化再取自变量前的系数作为aij；对于不可线性化的回归模型则具体问题具体分析。

3.3 计算影响因素之间的相关度

根据系统耦合理论，影响航空装备安全性除了四个主要因素之外，还要考虑因素之间的耦合交互作用。耦合程度用相关度描述，相关度可以是正也可以是负，可以是强相关也可以是弱相关。影响因素中人机、机环、人管和机管之间存在强相关(强耦合)作用，而环管间有弱相关(弱耦合)作用。强相关作用说明耦合交互的对象间相互影响和依赖的程度比较高，如人机交互就是一种强相关，它们之间存在人机行为交互和人机情感交互等耦合过程[10]。耦合作用越强，说明交互作用面越大，从而可能导致耦合风险也越大。用σij表示影响因素i和影响因素j之间的相关程度即耦合程度。

(1)

3.4 计算因素对于航空装备安全性的重要度

建立模型同时还要考虑因素对于航空装备安全性的重要度[8]。计算影响因素对航空装备安全性的重要度即计算影响因素对航空装备安全影响的权重。计算权重的方法有很多，其中层次分析法是一种比较常用的方法，考虑到层次分析法的局限性，本文采用序关系分析法来计算影响因素对航空装备安全影响的权重ηi。序关系分析法的计算分为以下三个步骤[11]：

(2)

(2)给出xk+1与xk间相对重要程度的比较判断。设专家评价指标xk+1与xk的重要性程度之比ωk-1/ωk的理性判断分别为

(3)

(3)计算各指标的权重系数。令

(4)

(5)

再按第(1)中的排序确定各指标的权重。

3.5 计算航空装备的安全度

在影响航空装备安全性的四个主要因素中，装备可靠度和管理科学可靠度的量值比较稳定，在某段不长的时间内可以认为是定值，而环境的适应可靠度和人的可靠度在遇到外界刺激时容易发生改变，并且后两者的改变很可能会影响前两者。为在计算航空装备的安全度之前能够比较精确的了解各因素之间的相互作用变化情况，使用冲量过程模型较好地描述并且预测各因素之间将来的变化情况[12]。

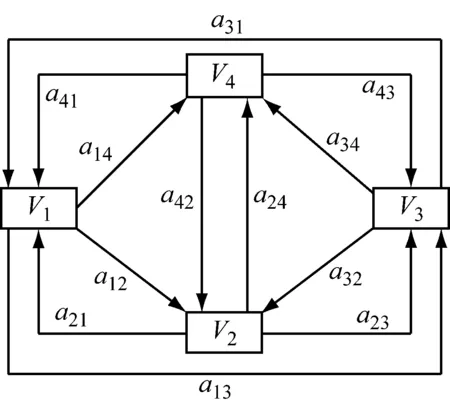
图1 影响因素冲量过程模型有向图

冲量过程为了研究某影响因素在初始时刻一个突然的变化所引起的整个因素系统在其后各时段的演变过程，用Ri(t)表示因素vi在时段t的可靠度，pi(t)表示vi在时段t的改变量(冲量)。影响航空备安全性共有4个因素，根据aij的含义显然有

(6)

式中:i=1,2,3,4;t=0,1,2,…;R(t)=(R1(t),R2(t),…,Rn(t)),P(t)=(p1(t),p2(t),…,pn(t))，则式(6)，(7)可表示为:

(8)

(9)

如果只考虑影响因素在初始状态基础上的变化，不妨设

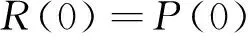
(10)

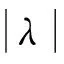
通过冲量模型可以计算出各影响因素在某时间段内的可靠度，航空装备的安全度可用下式计算

(11)

从上式可以看出,装备的可靠度和安全度之间有紧密的联系。如果装备的可靠度很低，即使其他因素的可靠度都很高，航空装备的安全度也不会很高，所以说装备的可靠度是系统安全度的基础；即使将装备的可靠度提高到1，航空装备的安全度也不可能达到1，也就是说提高装备的可靠度只能在一定范围内而不能无限制的提高航空装备的安全度[13]。

4 案例分析

针对我国某型飞机，结合该飞机在2010和2011两年的历史数据，分别计算影响度、相关度和重要度。结果见表1～3。

表1 某飞机各因素间影响程度

表2 某飞机各因素间相关程度

表3 某飞机各因素权重

假设某个时间段内该飞机的可靠度为0.999，人员可靠度为0.993，环境适应性为0.920，管理科学性为0.977.则飞机在诸因素影响下的安全度为：

S(t)=0.993×0.999×0.920×0.977+ 0.32×0.28×0.35×0.993×0.999+ 0.01×0.28×0.16×0.993×0.920+ 0.41×0.28×0.21×0.993×0.977+ 0.13×0.35×0.16×0.999×0.920+ 0.35×0.35×0.21×0.999×0.977+ 0.07×0.16×0.21×0.920×0.977= 0.891 6+0.031 1+0.000 4+0.023 3+ 0.006 7+0.025 1+0.002 1=0.980 3

当环境在飞机执行任务前突然发生改变，环境适应性由R3(t)=0.920降为R3(t+1)=0.850，由冲量过程模型[14-15]可得：

R1(t+1)=0.993-0.52×0.07=0.956 6

R2(t+1)=0.999-0.47×0.07=0.966 1

R4(t+1)=0.977-0.11×0.07=0.969 3

则飞机在t+1时刻执行任务时的安全度为

S(t+1)=0.956 6×0.966 1×0.85×0.969 3+ 0.32×0.28×0.35×0.956 6×0.966 1+ 0.01×0.28×0.16×0.956 6×0.85+ 0.41×0.28×0.21×0.956 6×0.969 3+ 0.13×0.35×0.16×0.966 1×0.85+ 0.35×0.35×0.21×0.966 1×0.969 3+ 0.07×0.16×0.21×0.85×0.969 3= 0.761 4+0.029 0+0.000 4+0.022 4+ 0.006 0+0.024 1+0.001 9=0.845 2

通过计算可知，环境适应可靠度的降低会在较大程度上影响航空装备的安全度，这并不是特例，任何一个因素的突变都会影响航空装备的安全度，所以单位要时刻关注各影响因素，以防某个或某几个因素的突然降低，使航空装备的安全度迅速下降，进而导致重大安全事故发生。

5 结 语

通过对能量意外释放论和轨迹交叉论的分析得出影响航空装备安全主要的因素，在此基础之上，对航空装备的安全性建模。结合案例分析可得出如下结论：

(1) 航空装备的安全性与可靠性有紧密的联系，但安全性并不等于可靠性。一方面可靠性是安全性的基础，如果航空装备的可靠性很低，那么其安全性必然不会高。另一方面，提高可靠性可以在一定程度上提高安全性，但超过了一定界限再提高可靠性对提高安全性并没有多少意义而且会浪费大量资源。

(2) 想要提高航空装备的安全性必须着力于提高所有影响因素的可靠性，单纯提高一方面，并不能有效地提高装备安全性。如在案例中制约飞机安全性提高的主要有环境和管理。对于环境，通过清扫和维护保持机场的干净整洁，提高飞机在起飞降落时的安全性；通过准确的天气预报可以避免飞机在极恶劣的天气飞行，提高飞机的使用安全性。对于管理，在民航中普遍使用的适航管理，可以有效地提高民航客机的安全性。两者必须同时进行，单纯提高某一方面，收效甚微。

[1] 张 栋.论安全和安全性[J].宇航材料工艺,2000(S):157-159.

[2] 舒文军,何宇廷,崔荣洪,等.一种基于条件概率的飞机安全性分析模型[J].航空精密制造技术,2009,45(6):53-57.

[3] 甘旭升，端木京顺，高建国，等. 基于ARIMA模型的航空装备事故时序预测[J].中国安全科学学报, 2012,22(3):97-102.

[4] 刘 瑞,马 麟,康 锐.基于PHM的航空装备可用度影响因素分析方法[J].北京航空航天大学学报，2011,37(10):1238-1244.

[5] 汪 送,王 瑛.基于脆性结构崩溃的复杂系统安全事故致因分析[J].中国安全科学学报，2011，21(5):138-142.

[6] 李万帮,肖东生.事故致因理论评述[J].南华大学学报(社会科学版),2007,8(1):57-61.

[7] 谈乐斌.浅谈人机系统可靠性[J].人类工效学,1999,5(4):47-49.

[8] 吕学志,于永利,张 柳.基于事件的系统可靠性参数仿真算法[J].火力与指挥控制,2012,37(4):73-78.

[9] 林嘉豪,李克武,张 兵.基于风险耦合理论的航空装备本质安全管理研究[J].中国安全生产科学技术,2011,7(9):75-79.

[10] 汪 送,王 瑛,李 超.一种航空装备系统中本质安全人的构建方法[J].工业安全与环保,2011,37(2):52-54.

[11] 孙鹤立,冯博琴,黄健斌,等.序关系优化的多超平面排序学习模型[J].模式识别与人工智能,2010,23(3):327-334.

[12] 姜启源,谢金星,叶 俊.数学模型[M].北京:高等教育出版社,2003.

[13] 郭 巍，王光辉，刘 奇.基于CGF的航空装备实验室建模技术研究[J]. 实验室研究与探索,2011, 30(5):159-165.

[14] 吴 伟,张凤鸣，惠晓滨. 航空装备技术保障指挥系统体系结构研究[J]. 空军工程大学学报2004,5(6):11-13.

[15] 魏宏博，陈云翔. 航空装备维修保障信息系统框架结构研究[J].计算机工程与设计, 2006,27(18):3413-3412.

Study on Model for Aviation Equipment Safety Analysis Based on Order Relation and Pulse Process Model

XINGNai-ruo,HUIXiao-bin,MENGXiang-fei

(Air Force Engineering University, Xi’an 710051, China)

Aiming at the problem of aviation equipment safety analysis’s complexity, the paper constructed a model to depict the safety of aviation equipment. Via analyzing energy unexpected release theory, orbit cross theory and manage fault theory, it concluded the mostly factors which impact the safety of aviation equipment. On the basis of these factors, the paper established a mathematical model by using system coupling theory, rank correlation analysis and pulse process model to describe the safety of aviation equipment. It found out the relation between safety and reliability as well as the approach to improve the safety of aviation equipment by construing the mathematical model and cases.

safety of aviation equipment; influence factors; system coupling theory; order relation analysis; pulse process model

2014-07-18

国家自然科学基金项目资助(60772162)

邢乃若(1990-)，女，河北定州人，硕士生，研究方向：系统工程。Tel.：185-3780-6565; E-mail：15029007368@163.com。

惠晓斌(1974-)，男，河南信阳人，博士，教授，研究方向：系统工程，智能决策，数据挖掘。

V 328

A

1006-7167(2015)03-0111-05