基于三维空间均匀矩形阵列的MIMO系统研究*
2015-02-21刘鹏,周杰,黄雷
刘 鹏,周 杰,黄 雷
(南京信息工程大学 电子与信息工程学院,江苏 南京 210044)
0 引言
在无线通信系统中天线阵列可以用来提升系统容量和信号质量,所以角度参数对天线阵列性能的影响很重要。波达信号的角域包括水平方位到达角(Azimuth of Arrival,AOA)和俯仰角(Elevation of Arrival,EOA)。 文献[1]中研究包含三维(three Dimensional,3D)天线阵列方法,假设方位到达角 AOA在[0,2π]上均匀分布,仰角则是不均匀地分布在水平面上。文献[1]中没有给出与水平方位到达角AOA、俯仰角EOA、天线阵列几何相关的闭合解析式。文献[2]中研究表明大约65%的入射信号相对于水平方位角平面仰角大于 10°。文献[3]中提到室内到室外几种环境中平均仰角扩展为9°。文献[4]研究表明均匀线阵(Uniform Linear Array,ULA)和均匀圆阵(Uniform Circular Array,UCA)下均匀分布和拉普拉斯分布的到达角概率分布函数和空间相关性函数,结果受限于方位平面。本文将研究方位到达角AOA和仰角EOA在均匀矩形阵列(Uniform Rectangular Array,URA)下对空间相关性的影响。
本文介绍了定向信道模型和均匀矩形阵列导向矢量(Steer Vector,SV),推导出在 3D均匀矩形阵列多种功率谱分布下空间衰落相关性的封闭形式表达式,分析AOA、EOA、方位角扩展(Azimuth Spread,AS)、俯仰角扩展(Elevation Spread,ES)及阵元间距对相关性的影响。采用多重信号分类(Multiple Signal Classification,MUSIC)算法对MIMO系统波达信号方向进行空间谱估计,推导了多种天线阵列空间谱通用公式。本文分析可以应用于多输入多输 出(Multiple Input Multiple Output,MIMO)系统容量分析以及MIMO系统的波达信号方向(Direction of Arrival,DOA)估计。
1 多天线信道模型
使用非频率选择性瑞利衰落信道模型分析天线阵列性能。信道脉冲响应表示为[5]:

其中,J是发射端天线总数量,aj(t)是发射端第j个天线复振幅,α(φj,θj)是均匀矩形阵列入射信号 矢量 ,这里 0≤φj<2π,0≤θj<π。 如图 1 所示,φj和 θj是发射端第j个天线的水平方位到达角和俯仰角。图1坐标系中xoy平面上设定一个N×P的均匀矩形天线阵列,入射信号矢量可以表示为[6]:
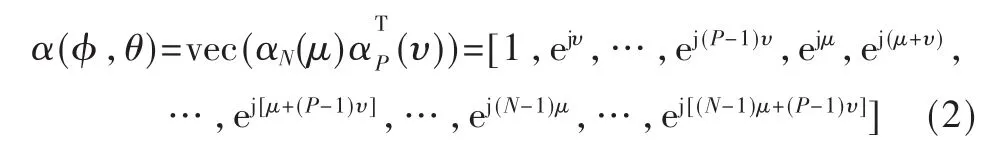
其中 μ=2πdxcosφsinθ/λ,υ=2πdysinφsinθ/λ,αN(μ)=[1,ejυ,…,ej(N-1)μ]T,αP(υ)=[1,ejυ,… ,ej(P-1)υ]T,[]T代表 转置符号,λ是波长。标量dx和dy分别是天线阵元与x轴和y轴的平行间距。指数n和p表示天线阵元位于均匀矩形阵列 URA第n行第p列,表示为(n,p)。
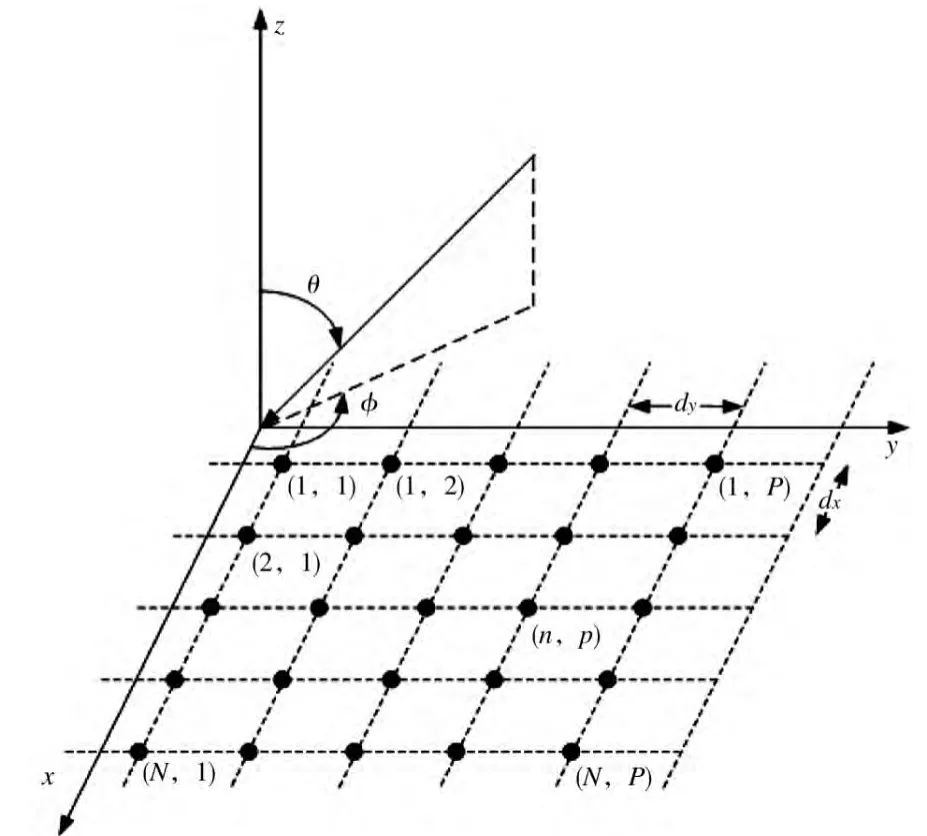
图1 均匀线性阵列URA三维空间接收模型
2 均匀矩形阵列空间衰落相关性
下面讨论在天线阵列为3D均匀矩形阵列时,均匀分布和高斯分布情况下的空间相关性。在均匀矩形阵列URA下,(n,p)和(m,q)两阵元之间空间相关性表示为:
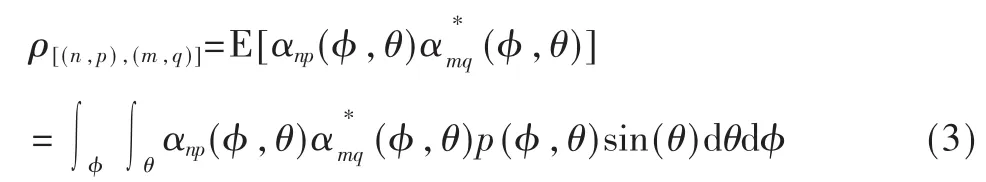
E[g]是期望运算符,上标*表示共轭复数,αnp(φ,θ)表示为(n,p)天线的入射信号。p(φ,θ)为接收端到达角概率分布密度函数,假设AOA和EOA是非相关的,函数p(φ,θ)可以表示为p(φ),p(θ)。
2.1 均匀分布情况下空间衰落相关性
假设波达信号水平方位角AOA和俯仰角EOA是均匀角能量分布函数。其函数表达式为:
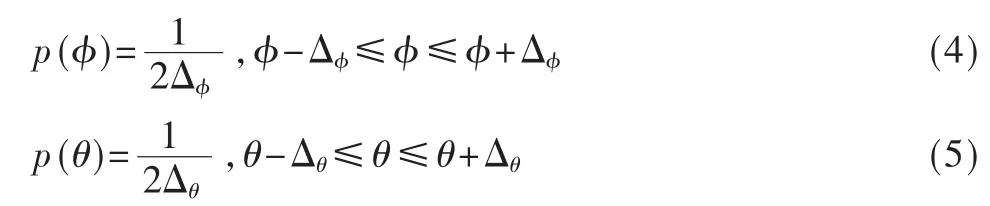
式中,2Δφ是 AOA方位角的范围,2Δθ是俯仰角 EOA的范围。根据式(3)可以进一步展开得到:
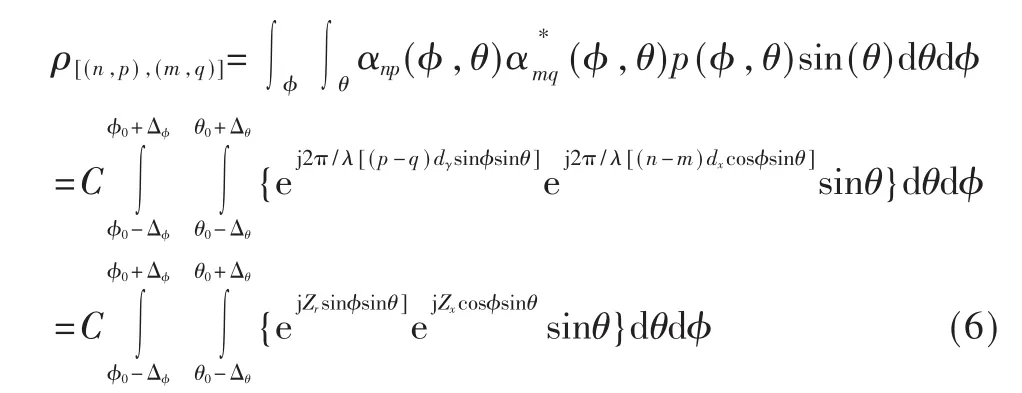
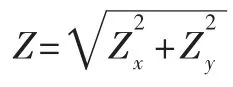
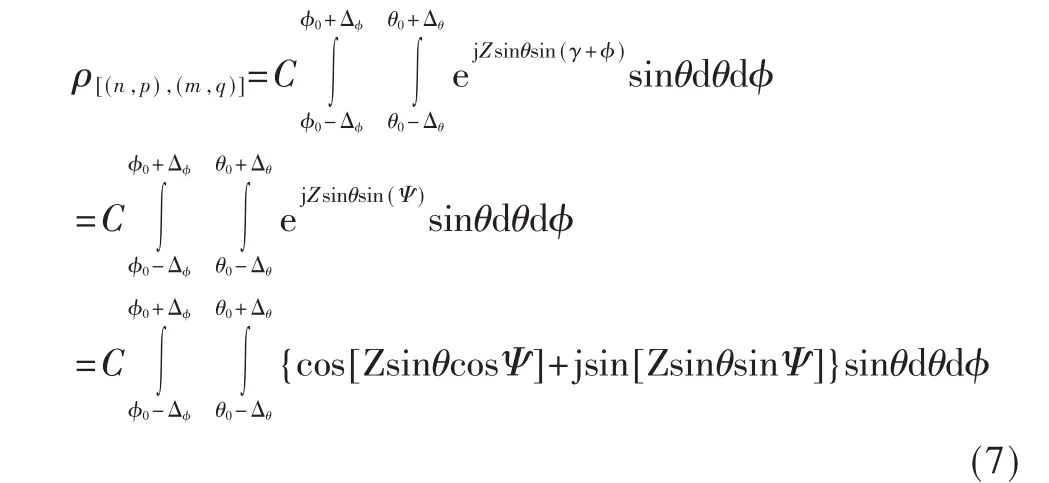
2.2 高斯分布情况下空间衰落相关性
假设波达信号水平方位角AOA和俯仰角EOA遵循高斯角能量分布[7]。其函数表达式为:
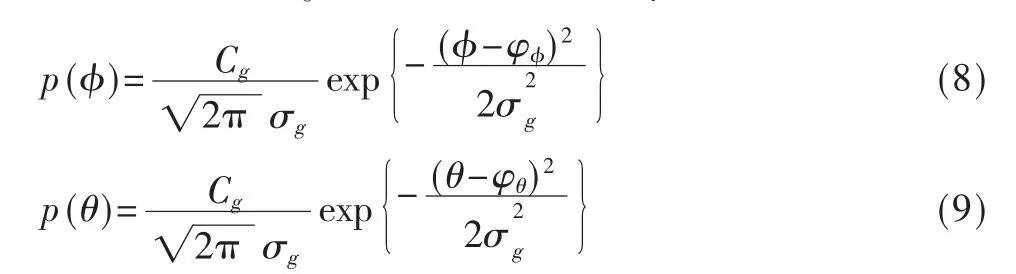
其中,σg是功率谱分布标准差,Cg是分布密度函数归一化常数。φφ是水平方位中心到达角,φθ是俯仰中心到达角。根据式(3)可以得到均匀矩形阵列 URA下,入射信号遵循高斯角能量分布时,两阵元之间空间相关性表达式:
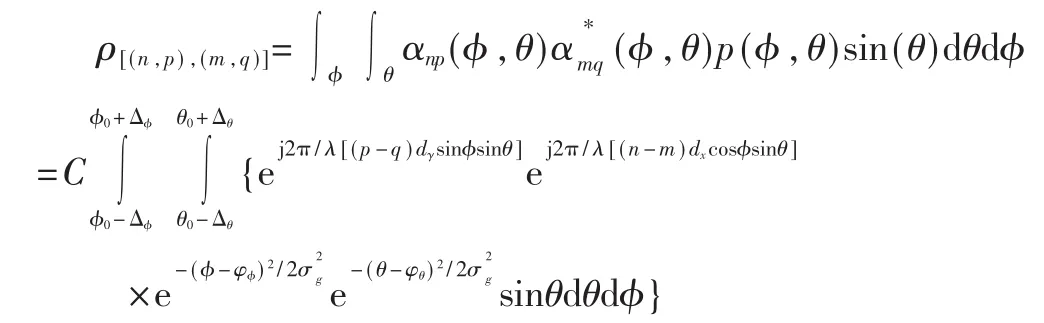
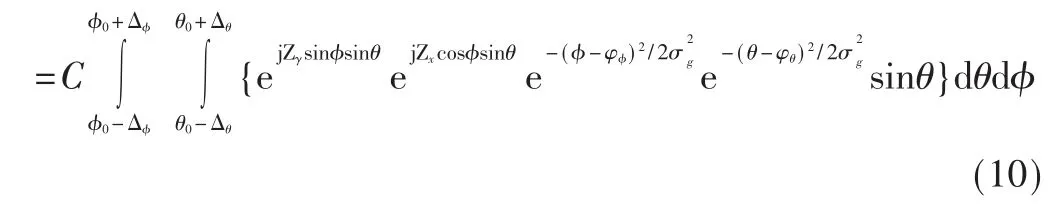
3 波达信号空间谱分析
空间谱是阵列信号处理中的重要概念,是信号在空间各个方向上的能量分布。本文利用MUSIC算法来分析URA下入射信号空间谱与其他天线阵列比较情况。MUSIC算法是利用接收数据协方差矩阵分离信号子空间和噪声子空间,通过正交性来构成空间扫描谱估计参数。假设有n信号入射到阵元数为p的天线阵列,n≤p,则其接收信号表达式为:
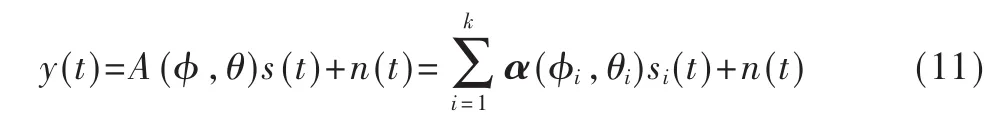
这 里 ,α(φi,θi)是 天 线 阵 列 信 号 导 向 矢 量 ,si(t)是 独立同分布窄带随机信号,n(t)是均值为0、方差为σ2平稳高斯白噪声。天线阵列为均匀线性阵列和均匀圆形阵列时,其入射信号导向矢量分别表示为:
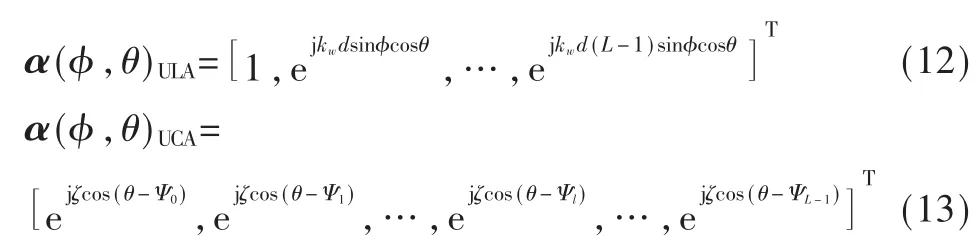
MIMO天线阵列信号自相关矩阵Ryy可表示为:
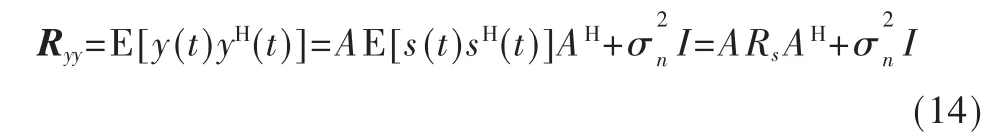
对式(14)进行特征分解可以得到:
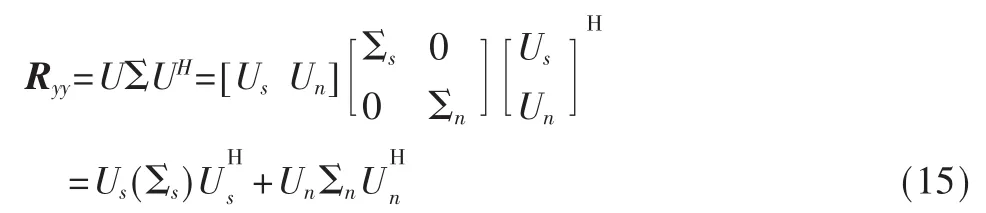
式中,Us是由大特征值对应的特征矢量张成的子空间也即信号子空间,而Un是由小特征值对应的特征矢量张成的子空间也即噪声子空间。假设信号子空间与噪声子空间正交,且波达信号为弱相关或不相关,通过MUSIC算法得到空间谱公式为[8]:
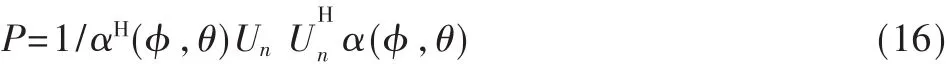
4 数值结果与分析
图2为入射信号遵循均匀分布时,俯仰角EOA和阵元间距对阵元(1,1)和阵元(2,2)之间空间相关性的影响。 设定 φ0和 θ0取 90°,AS为定值时,取 ES为不同值,比较两个阵元之间相关性对于阵元间距的变化。随着ES的增大,两阵元间相关性随之减小,随着阵元间距的增大,空间相关性减小。
图3所示为方位到达角AOA和阵元间距对两阵元间空间相关性的影响。 设定 φ0和 θ0取 90°,ES为定值时,取AS为不同值,比较两个阵元之间的相关性相对于阵元间距的变化。从图中可以明显看出,随着AS的增大,两阵元之间的相关性随之减小,同样随着阵元间距的增大,空间相关性减小。
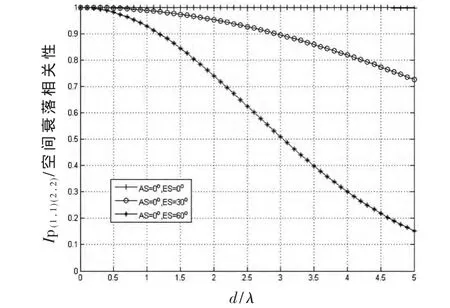
图2 均匀分布下AS=0°时d/λ和ES对空间衰落相关性的影响
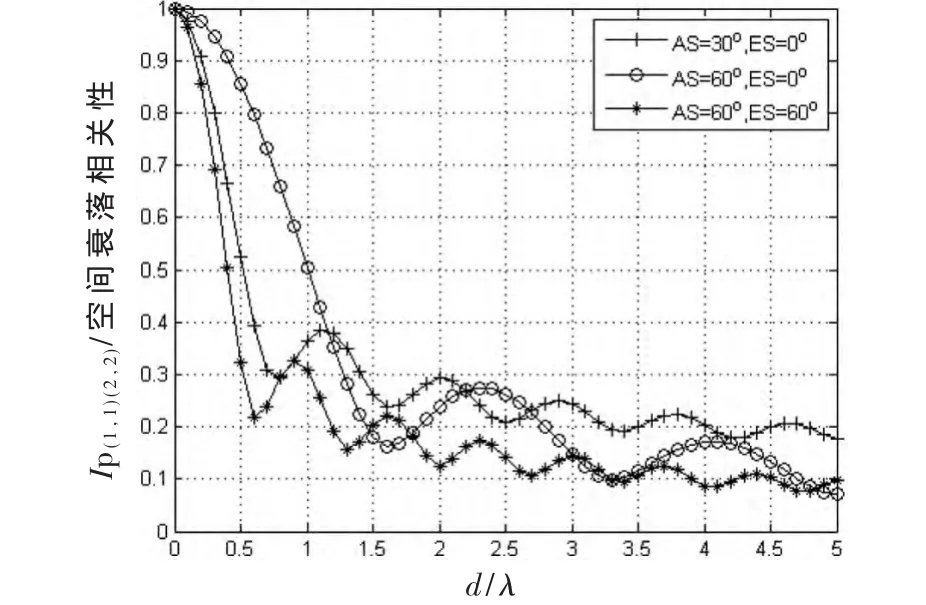
图3 均匀分布下ES=0°时d/λ和AS对空间衰落相关性的影响
图4所示为入射信号遵循高斯分布时,方位到达角AOA和阵元间距对两阵元间空间相关性的影响。当AS为0°时,取ES为不同值,比较两个阵元之间的相关性相对于阵元间距的变化。从图中可以看出随着ES的增加空间相关性减小。
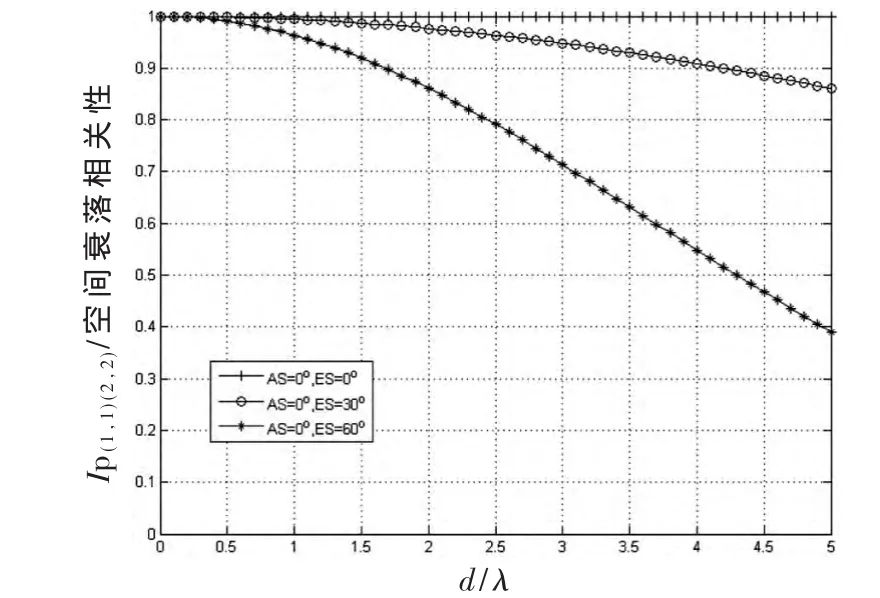
图4 高斯分布下AS=0°时d/λ和ES对空间衰落相关性的影响
如图5所示,入射信号遵循高斯分布时,方位到达角AOA和阵元间距对两阵元之间的空间相关性的影响。当 ES为 0°时,取 AS为不同值,可以看出随着AS的增加,空间衰落相关性下降的更快,结论与均匀分布情况下得出的结论一致。
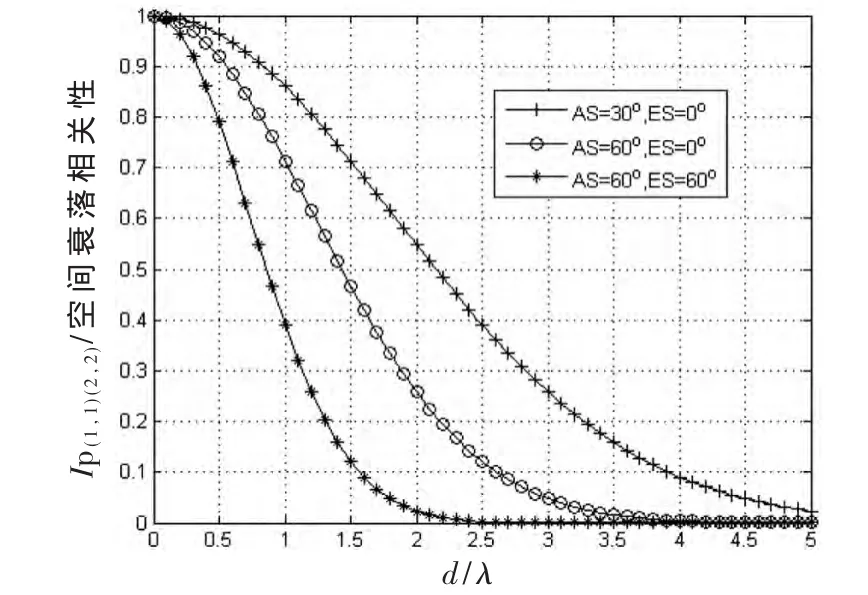
图5 高斯分布下ES=0°时d/λ和ES对空间衰落相关性的影响
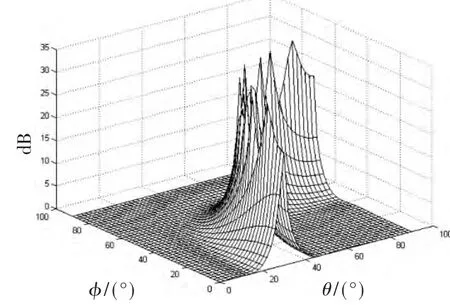
图6 均匀线性阵列下空间谱
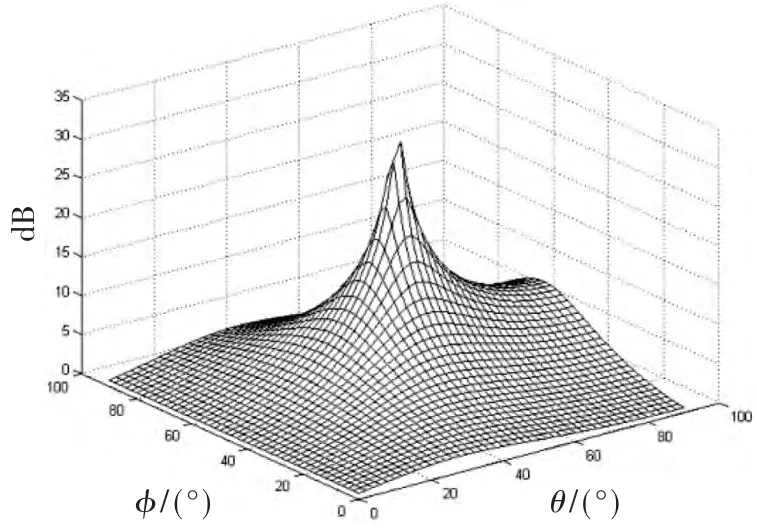
图7 均匀圆形阵列下空间谱
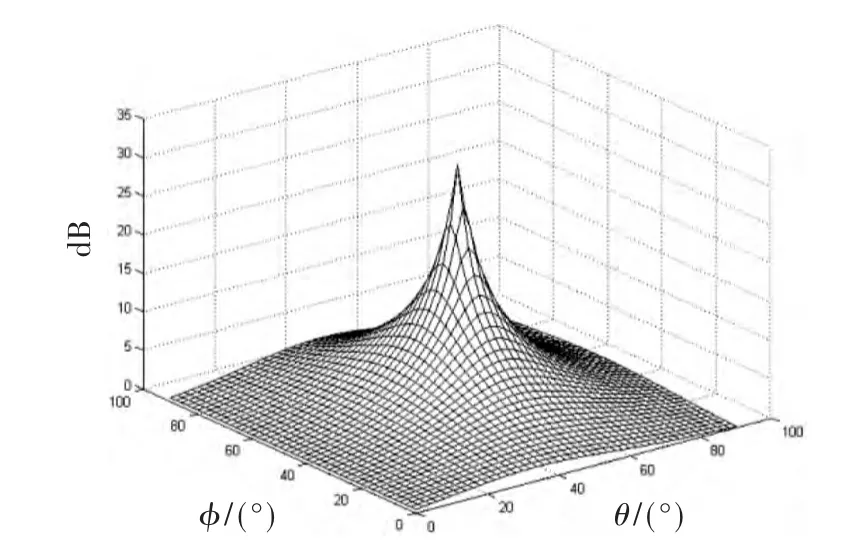
图8 均匀矩形阵列下空间谱
如图6~图8所示为MIMO天线阵列在分别采用ULA、UCA和URA情况下的空间谱分析仿真结果。假设有9个天线阵元,ULA阵元间距为d=0.5λ,UCA阵元半径r=0.5λ,URA阵元间距为dx=dy=0.5λ。 在到达角参数 φ和θ取相同值的情况下,入射信号在三维空间中进行定位时,会出现相位模糊情况。图6所示ULA空间为非均匀性,方向选择性强,所以波达信号的相位模糊比较严重,出现许多的MUSIC伪谱峰值。在图7和图8中可以看出,UCA和URA情况下相位模糊情况比ULA减弱,在θ角测向时可能出现一个伪谱峰值。所以分析空间谱时采用UCA和URA会得到更好的效果,趋向于无模糊定位。
5 结论
本文推导了三维多径信道中均匀矩形阵列URA在多种角能量分布下的空间衰落相关性解析公式,分析AOA、EOA、AS、ES以及阵元间距对空间衰落相关性的影响。采用多重信号分类MUSIC算法对MIMO系统波达信号方向进行空间谱估计,推导了多种天线阵列空间谱通用公式。通过计算机程序模拟仿真验证了分析结果,仿真结果表明方位角扩展AS和仰角扩展ES是天线相关性的主要决定因素,空间衰落相关性随着AS和ES的增加而减小。当AS和ES增加同样角度时,在AS增加的情况下,空间衰落相关性下降的更快,表明了AS对空间相关性影响更大。仿真结果还表明,采用同样的参数情况下估计MIMO系统空间谱,均匀矩形阵列URA相对于ULA和UCA更有优势。
[1]AULIN T.A modified model for the fading signal at a mobile radio channel[J].Vehicular Technology,IEEE Transactions on,1979,28(3):182-203.
[2]KUCHAR A,ROSSI J P,BONEK E.Directional macro-cell channel characterization from urban measurements[J].Antennas and Propagation,IEEE Transactions on,2000,48(2):137-146.
[3]KALLIOLA K,SULONEN K,LAITINEN H,et al.Angular power distribution and mean effective gain of mobile antenna in different propagation environments[J].Vehicular Technology,IEEE Transactions on,2002,51(5):823-838.
[4]TSAI J A,BUEHRER R M,WOERNER B D.Spatial fading correlation function of circular antenna arrays with Laplacian energy distribution[J].IEEE Communications Letters,2002,6(5):178-180.
[5]周杰,陈靖峰,邱琳.三维空间MIMO信道接收天线阵列互耦效应及系统容量分析[J].通信学报,2012,33(6):1-10.
[6]YONG S K,THOMPSON J S.Three-dimensional spatial fading correlation models for compact MIMO receivers[J].Wireless Communications,IEEE Transactions on,2005,4(6):2856-2869.
[7]ZHOU J,SASAKI S,MURAMATSU S.Spatial correlation functions for a circular antenna array and their applications in wireless communication system[J].IEICE Trans FUNDAM COMPUT SCI,2003,E86-A(7):1716-1723.
[8]SALIB F,SEDDIK K G.Exploiting spatial spectrum holes in multiuser MIMO systems[C].Signals,Systems and Computers,2013 Asilomar Conference on.IEEE,2013:1865-1868.
