基于改进希尔伯特黄变换的变压器励磁涌流识别

朱翔宇,王宝华

(南京理工大学 自动化学院,江苏 南京 210094)

基于改进希尔伯特黄变换的变压器励磁涌流识别

朱翔宇,王宝华

(南京理工大学 自动化学院,江苏 南京 210094)

变压器空载合闸或者短路故障切除后产生的励磁涌流会导致变压器差动保护误动作,因此需要对励磁涌流和故障电流进行识别。根据励磁涌流与故障电流的特点,前者中含有大量的二次谐波,研究了用改进希尔伯特黄变换方法对电流信号进行分解,根据分解后产生能量较大的IMF个数来区分励磁涌流和故障电流。改进希尔伯特黄变换方法用集成经验模态分解(EEMD)和经验模态分解(EMD)的组合,克服了经典法必然会出现模态混叠的问题,使信号能够被清晰的分解开来。经过Matlab仿真软件验证,该方法可以很好识别励磁涌流。

励磁涌流；二次谐波；改进希尔伯特黄变换；IMF；Matlab

变压器空载合闸和外部短路故障切除后电压恢复时所产生的涌流,可能会导致变压器的差动保护误动作。因此,对励磁涌流进行正确而有效的识别是一个亟待解决的问题。许多学者针对此问题做了大量研究。目前应用的识别原理主要是基于波形特征的方法。这种方法是以励磁涌流和内部故障电流波形特征的差异为依据,主要是利用以下两种原理,即二次谐波制动原理和间断角原理［1］。文献［2］提出利用励磁涌流波形具有间断角的特征进行识别可能会由于变压器铁芯材料的改进,剩磁,合闸角以及电流互感器的传变的影响,间断角可能变形甚至消失,使得这些保护判据受到影响。

而根据二次谐波制动原理进行励磁涌流识别在实现时需要滤波技术从电流信号中分离出基频分量和二次谐波分量。常用的电力系统信号分析方法中傅里叶变换能够在频域内得到较高的分辨率,在时域内却失去了分辨能力。小波变换能够在时域和频域内同时得到较高的分辨率,但也存在基函数的选择的问题。文献［3］提出了一种信号处理新方法——经典希尔伯特黄变换（Hilbert-Huang Transform,HHT）。这种方法采用了固有模态函数（Intrinsic Mode Function,IMF）概念以及将任意信号分解为IMF组成的思想,即经验模态分解（Empirical Mode Decomposition,EMD）,使得瞬时频率具有实际的物理意义［5-6］。但是,经典希尔伯特黄变换本身会发生的模态混叠现象。文献［7-10］提出了一种噪声辅助信号分析新方法,即聚类经验模态分解 （Ensemble Empirical Mode Decomposition, EEMD）,利用EEMD取代EMD进行分解。该方法将白噪声加入信号来补充一些缺失的尺度,从而克服模态混叠现象。

本文在用EEMD取代EMD进行改进的基础上提出对信号EEMD分解后进行部分重组,再利用EMD分解的两次分解方法,改进了经典希尔伯特黄变换。本文运用此方法,提出根据分解后在Hilbert谱中提取出能量较大的IMF的个数来对励磁涌流进行识别的判据。经过Matlab仿真结果分析,改进希尔伯特黄变换对励磁涌流能够进行很好地识别。

1 经典HHT与改进HHT简介

1.1 Hilbert变换

时间信号x（t）的Hilbert变换表示为:

将x（t）和y（t）组成解析信号z（t）:

从而得到了信号的瞬时幅值、相位和频率:

1.2 固有模态函数(IMF)

希尔伯特黄变换中的重要概念——固有模态函数（IMF）的主要目的是使得Hilbert变换得到的瞬时频率能够反映信号所含的物理机制。固有模态函数需要满足以下两个条件:

1）在信号的整个持续时间内,零交点的数目与极值点的数目必须相等或至多相差1；

2）在任意时刻,由局部极大值点定义的上包络线和局部极小值点定义的下包络线之间的平均值为零。

1.3 Hilbert谱

对每个IMF作Hilbert变换得到

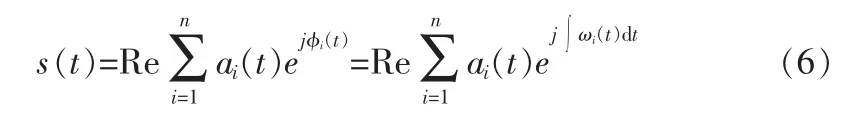
式（6）称为Hilbert谱,记作

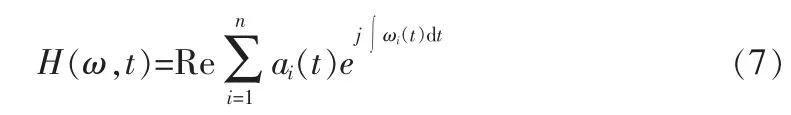
1.4 经验模态分解(EMD)

经验模态分解 （EMD）就是把 IMF筛选出来的过程（Sifting Process）。具体分解过程如下:

1）给定信号x（t）,寻找x（t）的所有局部极值点。对极值点进行拟合从而得到信号的上下包络线分别记为 xmax（t）、xmin（t）,使x（t）满足xmin（t）≤x（t）≤xmax（t）。

2）记m1（t）为上、下包络线的均值,即m1（t）=［xmax（t）+xmin（t）］/2。

3）用原序列x（t）减去m1（t）,得到一个新序列h1（t）,即h1（t）=x（t）-m1（t）。如果h1（t）满足IMF的定义,那它就是第一个固有模态函数,否则,把h1（t）当作原序列,找到h1（t）的包络平均值m1,1（t）,计算h1（t）与m1,1（t）的差得到:h1（t）-m1,1（t）=h1,1（t）。重复以上步骤k次,直到当h1,k（t）满足IMF的两个条件,得到第一个IMF,记c1（t）=h1,k（t）。

4）用原序列x（t）减去 c1（t）,得到剩余值序列r1（t）,即r1（t）=x（t）-c1（t）。

5）把剩余值序列r1（t）作为一个新的原序列,按照以上步骤,依次提取直到第个固有模态函数cn（t）,提取最后一个固有模态函数之后,rn（t）变成一个单调序列。

如果把各IMF分量合并起来,就得到原序列x（t）。

经典希尔伯特黄变换的关键EMD是按照特征时间尺度对信号进行分解。但是,如果信号中包含有噪声,分解时可能就会缺失一些尺度,这样就出现了模态混叠现象。所谓模态混叠,即一个IMF分量包括了尺度差异较大的信号,或是一个相似尺度的信号出现在不同的IMF分量中。在实际工程中,所有数据都是信号中夹杂了噪声的干扰。因此,经典希尔伯特黄变换的模态混叠现象是不可避免的,这就是其主要缺陷。

1.5 改进希尔伯特黄变换

为了解决模态混叠问题,有学者提出了一种噪声辅助数据分析方法EEMD。它是把一个全体测试的均值定义为真实的IMF分量,每个都包含了信号和有限幅值的白噪声。EEMD过程如下:

1）向信号加入正态分布白噪声。

2）将加入白噪声的信号分解成各IMF分量。

3）重复步骤（1）（2）,每次加入新的白噪声序列。

4）将每次得到的IMF集成均值作为最终结果。

然而,EEMD构成的二进滤波器组相邻两个滤波器之间会有一定的频带重合部分,因此,当信号数据中包含的两个模态的固有频率非常相近时,会有少量的能量泄露在相邻的分解分量中。

本文提出的改进希尔伯特黄变换是将EEMD分解作为一个二进滤波器,再利用EMD方法对第一次EEMD的结果进行再处理,即将模态相同的相邻分量重新组合后再进行EMD分解,最后做出Hilbert谱进行谱分析。这样避免了模态混叠的问题,从而可以提取出带有物理意义的IMF分量。

2 励磁涌流识别判据

2.1 故障电流分解特性

根据电路叠加原理,故障点的电流是正常分量和故障分量的叠加。电力系统发生故障时的故障分量是远大于正常分量,因此故障点电流可以忽略正常分量,只看成故障分量的电流。故障电流含有较少的非周期分量,没有呈现出尖顶波凸凹特性,含有二次谐波为主的高次谐波较少。因为故障电流基本保持了基频正弦波特征的特点,所以对故障电流进行希尔伯特黄变换后,Hilbert谱上只有一个能量较大的IMF分量,即基频分量。

2.2 励磁涌流分解特性

三相变压器产生的励磁涌流中含有大量的高次谐波分量,并且以二次谐波为主。同时三相励磁涌流有可能出现一相或两相的二次谐波含量较小,但至少会有一相比较大。由于有基频分量和大量二次谐波分量的存在,对励磁涌流进行希尔伯特黄变换后,通过Hilbert谱可以观察到多个能量较大的IMF分量。

2.3 识别判据

首先输入三相电流波形信号,利用改进希尔伯特黄变换的方法对电流信号进行分解,并且做出Hilbert谱。利用Hilbert谱进行观察,如果至少有一相的电流分解后出现多个能量较大的IMF时,那么就可以判断为励磁涌流,否则为内部故障电流。

3 仿真分析

3.1 变压器短路故障切除

本文应用Matlab中的Simulink进行建模仿真。仿真模型如图1所示。

图1 变压器短路故障模型Fig.1 Model of short circuit fault of transformer

变压器短路故障的仿真时间设为5s,在A相合闸角为0°和A、B、C三相剩磁为0.6,0.6,0的条件下,系统在4.2s时发生三相短路,4.5s时将短路故障切除。由于在实际工程状况下测得的信号会含有噪声的干扰,得到短路故障切除后三相励磁涌流的差流波形如图2所示。

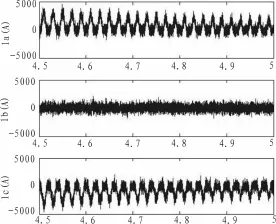
图2 三相励磁涌流差流波形Fig.2 Differential current waveform of three phase inrush current

由图2可以看出,B相涌流为对称性涌流,A、C两相为非对称性涌流。由于对称性励磁涌流的数值比较小,故对A、C两相的励磁涌流差流使用改进希尔伯特黄变换方法进行判据验证。在进行EEMD分解时,选择添加噪声幅值比为0.1,总体个数为50。

以C相为例,C相励磁涌流EEMD分解如图3所示。

图3 C相励磁涌流EEMD分解结果Fig.3 EEMD of C phase inrush current

对C相励磁涌流EEMD分解结果进行分析,c1到c5为EEMD对白噪声的分解,c6到c9认定为信号的主模态。由于在EEMD分解中不同模态之间有能量的泄漏,将c6到c9分量进行重新组合,再对重新组合的信号进行EMD分解,并做出Hilbert谱,如图4所示。

Hilbert谱中IMF分量能量大小的区分通过显示的颜色深浅进行区别。对Hilbert谱进行分析,C相电流经过改进希尔伯特黄变换分解出多个能量较大分量的IMF,其中包括有能量较大的50 Hz基频分量和以二次谐波为主的谐波分量。根据识别判据可以判断此电流为励磁涌流。用同样的方法对A相电流进行分解,可以得到类似的结论。

3.2 变压器空载合闸

变压器空载合闸仿真模型与图2类似,通过将短路故障模型中的变压器二次侧空载而得到。设置A相合闸角为0°, A、B、C三相剩磁（标幺值）分别为0.6,0.6,0,三相励磁涌流差流波形如图5所示。

由变压器空载合闸三相励磁涌流的差流波形,同样也出现了非对称性涌流和对称性涌流。对A、C两相非对称性励磁涌流差流使用改进希尔伯特黄变换方法进行分解。电流信号中同样含有噪声,因此,在EEMD分解过程中添加白噪声的幅值比为0.1,总体个数为50。

以A相为例,A相励磁涌流进行EEMD分解如图6所示。

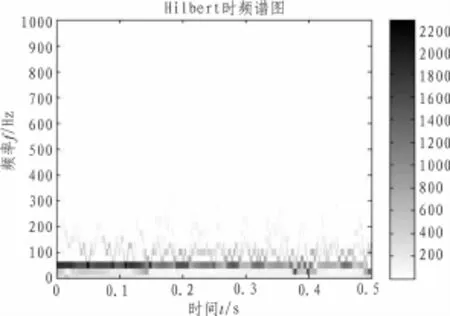
图4 C相励磁涌流Hilbert谱Fig.4 Hilbert spectrum of C phase inrush current

图5 三相励磁涌流差流波形Fig.5 Differential current waveform of three phase inrush current

图6 A相励磁涌流EEMD分解结果Fig.6 EEMD of A phase inrush current

对A相励磁涌流分解结果进行分析,可以看出c1到c5为EEMD对白噪声的分解,而c6到c9可以认定为信号的主模态。将c6到c9分量进行重新组合,再进行EMD分解,做出Hilbert谱,如图7所示。通过Hilbert谱可以看出A相励磁涌流分解出IMF有多个较大分量,并可以观察到其中两个主要的IMF分量频率分别为50 Hz和100 Hz。

图7 A相励磁涌流Hilbert谱Fig.7 Hilbert spectrum of A phase inrush current

A相电流差流波形经过改进希尔伯特黄变换分解出两个能量较大分量的IMF,由判据可以判断A相电流为励磁涌流,验证了励磁涌流识别判据。用同样的方法对C相电流进行分解,可以得到类似的结论。

3.3 变压器内部故障

当变压器内部发生两相短路时,用改进希尔伯特黄变换方法做出三相故障电流的Hilbert谱,其中A相电流结果如图8所示。

图8 A相励磁涌流Hilbert谱Fig.8 Hilbert spectrum of A phase inrush current

经分析,三相故障电流通过改进希尔伯特黄变换分解出的IMF中都只有一个较大的分量,并且可以观察到该分量确为50 Hz的基频分量。根据本文提出的识别判据,认为是故障电流,从而再次验证了励磁涌流识别判据。

4 结 论

本文研究了利用改进希尔伯特黄变换来识别变压器励磁涌流。与经典法相比,改进法能克服EMD天生的缺陷,较为理想地去除模态混叠。针对故障电流和励磁涌流的分解特性,指出了故障电流与励磁涌流区别的明显特征:前者只有一个较大的IMF分量,而后者能分解出多个较大的IMF。仿真实验结果表明改进希尔伯特黄变换方法能够清晰的将信号分解出来,可以很好识别励磁涌流和故障电流。

［1］张保会,尹项根.电力系统继电保护［M］.北京:中国电力出版社,2009.

［2］倪良华,姚春球.故障电流与励磁涌流的EMD特性分析［J］.电力系统保护与控制,2009,37(10):27-32.NI Liang-hua,YAO Chun-qiu.Characteristics analysis of fault current and inrush based on EMD［J］.Power System Protection and Control,2009,37(10):27-32.

［3］刘德利.HHT算法及其在电力系统中的应用研究［D］.哈尔滨:哈尔滨工业大学,2011.

［4］贾春花.希尔伯特-黄变换及其在信号处理中的应用研究［J］.电力学报,2012,556(49):47-50.JIA Chun-hua.Study of Hilbert-huang transform and its applications in signal processing［J］.Journal of Electric Power, 2012,556(49):47-50.

［5］李天云,赵妍,季小慧,等.HHT方法在电力系统故障信号分析中的应用［J］.电工技术学报,2005,20(6):87-91.LI Tian-yun,ZHAO Yan,JI Xiao-hui,et al.Application of HHT method for analysis of fault signal in electric power system［J］.Transactionsof ChinaElectrotechnical Society,2005, 20(6):87-91.

［6］刘德利,曲延滨,梁景凯.希尔伯特-黄变换在电力谐波分析中的应用研究［J］.电测与仪表,2011,546(48):39-43.LIU De-li,QU Yan-bin,LIANG Jing-kai.Application research of HHT in harmonic analysis of power system［J］.Electrical Measurement&Instrumentation,2005,20(6):87-91.

［7］焦彦军,胡春.基于改进EEMD方法的数字滤波器［J］.电力自动化设备,2011,31(11):64-68.JIAOYan-jun,HUChun.Digital filter based on improved EEMD method［J］.Electric Power Automation Equipment, 2011,31(11):64-68.

［8］时世晨,单佩韦.基于EEMD的信号处理方法分析和实现［J］.现代电子技术,2011,34(1):88-94.SHI Shi-chen,SHAN Pei-wei.Signal processing method based on ensemble empirical mode decomposition［J］.Modern Electronics Technique,2011,34(1):88-94.

［9］陈可,李野,陈斓.EEMD分解在电力系统故障信号检测中的应用［J］.计算机仿真,2010,27(3):263-266.CHEN Ke,LI Ye,CHEN Lan.Ensemble empirical mode decomposition for power quality detection applications［J］.Computer Simulation,2010,27(3):263-266.

［10］朱宁辉,白晓民,董伟杰.基于EEMD的谐波检测方法［J］.中国电机工程学报,2013,33(7):92-98.ZHU Ning-hui,BAIXiao-min,DONG Wei-jie.Harmonic detection method based on EEMD ［J］.Proceedings of the CSEE,2013,33(7):92-98.

Identification of power transformer inrush current based on improved Hilbert-Huang transform

ZHU Xiang-yu,WANG Bao-hua
（School of Automation,Nanjing University of Science&Technology,Nanjing 210094,China）

Inrush currentmay lead to a false action of the differential protection.In that case,the identification of inrush current and fault current is needed.According to the characteristic of inrush current and fault current,inrush current contains a large component of second harmonic.The decomposition,based on improved Hilbert-Huang Transform,of a current signal into IMF is studied.And according to the number of larger IMF,inrush current and fault current can be distinguished.The improved Hilbert-Huang Transform combines EEMD with EMD in order to overcome the mode mixing problem,which cannot be avoidedby the classic Hilbert-Huang Transform.Thus,it can decompose the signals clearly.It is proved by Matlab simulation that this method can identify inrush current well.

inrush current；second harmonic；improved Hilbert-Huang transform；IMF；Matlab

TN919.5

：A

：1674-6236（2015）18-0148-05

2014-11-28稿件编号：201411245

朱翔宇(1989—),男,江苏南京人,硕士研究生。研究方向:电力系统继电保护。