基于混合分布估计算法的智能配钞策略
2015-02-21罗攀峰梁添才徐俊
罗攀峰,梁添才,徐俊
(广州无线电集团,广州广电运通金融电子股份有限公司,ATM研究院,广东 广州510663)
基于混合分布估计算法的智能配钞策略
罗攀峰,梁添才,徐俊
(广州无线电集团,广州广电运通金融电子股份有限公司,ATM研究院,广东 广州510663)
目前金融自助设备采用钞箱或者鼓存放现钞,每一个钞箱或者鼓只存放一种面额,为减少钞箱数量和节省硬件制造成本,实现一个钞箱或鼓存放多个面额,是钞箱设计技术的发展趋势之一,因而实现自助设备存在一个或多个钞箱或存储鼓同时存放有多种不同的面额情况下的配钞是一个组合优化问题。针对该组合优化问题,本文建立了相应组合优化问题的线性规划数学模型,并提出了一种基于混合分布估计算法(HEDA)的智能配钞策略。通过实验仿真表明新的智能配钞算法的有效性。
金融自助设备;分布估计;钞箱;配钞策略
目前鼓式循环机芯只针对人民币采取1种面额的纸币需要1个鼓的配置方法,而对于混存及鼓少于币种面额方案没有加于考虑,鼓本预研计划考虑面额数量大于鼓个数的情况,比如欧元有7个面额,如只用4个鼓如何处理,及需要考虑混存和配置缓存区的情况,并提出几种方案的优劣势对比分析。提出多种鼓式循环机芯配钞方案,考虑多种应用环境。
为减少钞箱数量,节省硬件制造成本,实现一个钞箱或鼓存放多个面额,是钞箱设计技术的发展趋势之一,因而实现自助设备存在一个或多个钞箱或存储鼓同时存放有两种不同的面额情况下的配钞是必要的。
本文提出了基于混合分布估计算法的多种智能配钞方案,考虑多种应用环境,能提供取款的多种数额,考虑多种应用环境。该智能配钞策略是基于混合粒子群算法的优化策略,通过引入分布估计算法(EDA)的建立概率模型和随机采样的思想,保证算法整体算法收敛性,另外通过引入遗传算法的交叉和变异操作思想来避免算法陷入局部最优解。最终通过实验仿真结果表明,在混合分布估计算法在求解钞箱混合面额配钞优化问题具有很好的效果。
1 钞箱混合面额配钞优化问题
钞箱混合面额配钞优化问题是一个复杂的组合优化问题。为了描述方便,先对钞箱混合面额配钞优化数学建模。首先设定的自助设备配备有m个混合面额钞箱和n个单一面额钞箱,K表示钞箱能装钞票的张数上限。给定取款数额C,aij表示第i个混合面额钞箱中第j张钞票的面额,bij表示第i个单个面额钞箱中第j张钞票面额,如何选择出钞方案,使得出钞的总额度最接近取款额度?其目标函数为:
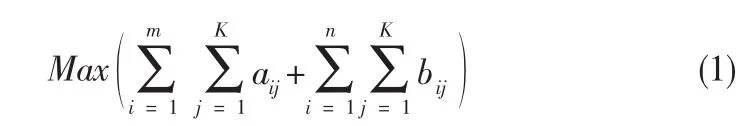
约束条件为出钞的累积面额不能超过取款额度,即

2 本文算法描述
分布估计算法(EDA)[1-3]是遗传算法[4-7]和概率统计的相互结合,根据进化过程中优质解信息的概率分布模型产生新解,具有概率分析的数学理论基础。本文混合分布估计算法(HEDA)的基本框架如下:
第一步:选择,初始种群是通过随机产生的解中挑选出优良解组成;
第二步:建模,利用建立数学的概率模型来计算出种群的优劣并产生新解;
第三步:变异,采用随机选取某位进行变异操作;
第四步:替换,将产生的新解加入新种群替换旧解;
第五步:判断是否满足终止条件。若满足则结束,新种群的解即为所求解;否则转至第二步;
分布估算法的核心算子是概率模型的建立。在分布估计算法中,表示解空间分布的概率模型是一个概率向量即p(x)=(p(x1),p(x2),…,p(xn)),其中p(xi)表示位置i上取值1的概率。概率模型的计算公式如下:

其中,pj(x)表示第j次种群解空间的概率向量,表示N个优质解,表示位置i上的取值,a表示学习因子。
3 实验仿真及结果分析
假设出钞机芯有3个混合钞箱:a1j(面额值为2和5)、a2j(面额值为10和20)、b1j(面额值为50)。二个混合钞箱依次存放钞票的信息为:

表1 钞箱现有钞票信息Tab.1 a1jbanknotes information

表2 a2j钞箱现有钞票信息Tab.2 a2jbanknotes information
用本文提出的混合分布估计算法来求解该问题,含有交叉操作的分布估计算法(HEDA)和传统的分布估计算法作了性能比较,各算法在计算机上迭代40次,当要求出钞额度1 029时,目标函数收敛曲线如图1所示。
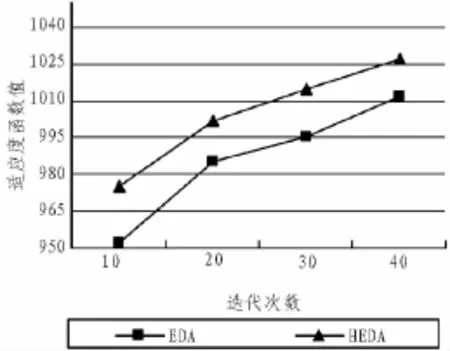
图1 算法寻优能力比较Fig.1 Search capability comparison
从图1基本能看出本文的混合分布估计算法能更开的寻找到更佳的近似最优解。并且在算法的整个迭代过程中,HEDA算法由于引入交叉等操作使得算法保持较好的种群多样性,从而使得HEDA算法比EDA算法具有更好的寻优能力。
4 结论
文中针对智能配钞的组合优化问题建立了相应组合优化问题的线性规划数学模型,并提出了一种基于混合分布估计算法(HEDA)的智能配钞策略。通过实验仿真表明新的智能配钞算法提供更好的资源利用率和寻优能力,充分地说明了算法的有效性和可靠性。
[1]Shapiro J L.Drift and scaling in estimation of distribution algorithms[J].Evolutionary Computation,2005,13(1):99-123.
[2]周树德,孙增炘.分布估计算法综述[J].自动化学报,2007,33(2):113-124.ZHOU Shu-De,SUN Zeng-Qi.A survey on estimation of distribution algorithm[J].Acta Automatic Sinica,2007,33(2): 113-124.
[3]刘明芳.基于分布估计算法的整数规划研究[D].武汉:武汉理工大学,2008.
[4]云庆夏,黄光球,王站权.遗传算法和遗传规划[M].北京:冶金工业出版社,1997.
[5]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,2000.
[6]张文修、梁怡编.遗传算法的数学基础[M].西安:西安交通大学出版社,2003.
[7]蒋磊,邹兵,吴明.基于改进免疫遗传算法的含分布式电源配电网规划[J].陕西电力,2012(10):26-30.JIANG Lei,ZOU Bing,WU Ming.Distribution network planning with distributed generation based on improved immune genetic algorithm [J].Shaanxi Electric Power,2012 (10):26-30.
Intelligent allocation strategy of currency based on estimation of distribution algorithm
LUO Pan-feng,LIANG Tian-cai,XU Jun
(ATM Research Institute,GRGBanking,Guangzhou Radio Group,Guangzhou 510663,China)
The current financial self-service equipment using money box or drum storage notes,each note box or drum store only one denomination,in order to reduce the cash box number and save hardware cost,the realization of a cash box or drum store multiple denominations,is the development trend of the design technology of money box,thus realizing self-service equipment there one or more cash box or storage drum at the same time deposit with bank note denomination of a variety of different conditions is a combinatorial optimization problem.In view of this combinatorial optimization problem,the paper establishes the mathematical model of linear programming corresponding combinatorial optimization problems,and propose a hybrid estimation of distribution algorithm based on(HEDA)smart with money policy.Simulation results show that the effectiveness of the new algorithm intelligent allocation of money.
hadoop;estimation of distribution;particle swarm optimization;mapreduce
TN18
:A
:1674-6236(2015)18-0004-02
2014-12-16稿件编号:201412128
国家863计划重大项目智能云服务与管理平台核心软件及系统(2013AA01A212);国家科技支撑计划课题电子信息产业集群质量保障服务平台应用示范(2012BAH27F05);广东省自然基金团队研究项目云计算核心技术及云服务应用研究(S2012030006242)
罗攀峰(1976—),男,湖南株洲人。研究方向:ATM智能配钞,企业信息化等。
