Vassiliev不变量与纽结的相似性
2015-02-21霍承刚
霍承刚
(宿州学院 数学与统计学院,安徽 宿州 234000)
v(KD)=v(K+)-v(K-)
.
,
.
,
,
.
Vassiliev不变量与纽结的相似性
霍承刚
(宿州学院 数学与统计学院,安徽 宿州 234000)
介绍一类重要的纽结不变量,即Vassiliev不变量,且利用纽结的相似性研究了其一些重要性质.
纽结; 琼斯多项式;Vassiliev不变量; 相似性
纽结理论与分子生物学、理论物理、化学等自然科学领域密切相关,例如近20年来在生物体和实验室合成出许多拓扑新颖的分子纽结和分子环链.Birman和Lin给出了Vassiliev不变量的公理描述.本文采用Birman-Lin所引进的Vassiliev不变量的定义[1]. 纽结的Vassiliev不变量是一个特色鲜明的不变量,有类似多项式的性质等.研究者刻画Vassiliev不变量的特性的角度方法逐渐增多[1-8],比如,Ohyama[2]运用纽结的相似性进行刻画;Stanford[3]运用辫交换子研究其性质,Ohyama和Yamada[4]结合Cn-move来研究等.
1 预备知识
对于值域是Abel群的纽结不变量,运用下述线束关系
v(KD)=v(K+)-v(K-)
来定义奇异纽结的不变量,KD,K+,K-代表局部如图1所示,但其他部分相同的纽结图表.

定义1 设v为值域在Abel群的纽结不变量,若对任意多于n个奇异点的纽结K有v(K)=0,则称不变量为n阶Vassiliev不变量,记为vn.
例 令L=L1∪L2∪…∪Ln表示有序定向的n-分支环链,λij(L)为1阶的Vassiliev不变量,其中λij(L)表示Li与Lj(i 定理1 令λijλkl(L)=λij(L)λkl(L),则λijλkl是2阶的Vassiliev不变量. 事实上,设vd和ve分别为d阶和e阶的Vassiliev不变量,则vdve为d+e阶的Vassiliev不变量. 因为纽结的Conway多项式中二次项的系数是2阶的,所以有6种2阶的Vassiliev不变量:常数,φi(1≤ i≤n),λij(i 定理2 令a,bi,cij,dij,eijk,fijkl为常数,则 为n分支环链L的2阶的Vassiliev不变量. 引理1 对纽结K及自然数n,存在无限多个纽结与K具有相同m(1≤m≤n)阶不变量. 定义2 设K为纽结,D(K)是K的图表,令C为D(K)中交叉点的集合,n为正整数,设A={A1,A2,…,An}为n个C的不交非空子集的集合.用Aj1j2…jm记子集{Aj1,Aj2,…,Ajm}.若对A的每个非空子集Aj1j2…jm中元素交换交叉点,都可得到固定纽结L,那么称K与L是n-相似的.特殊地,若L为平凡纽结,K称为 n-平凡的. 引理2 对任意自然数n>1,存在无穷多个纽结为n-平凡的却不是n+1平凡的. 引理3[5]对任意纽结L和自然数n,有无穷多个复合纽结相似于L. 设K为n-相似于L的纽结,D(K)是K的图表,并且{A1,A2,…,An}给出K与L的相似性. 定理3 设K为纽结,则K与任意有限个(n+1)-平凡纽结的连通和同K拥有相同阶≤n的Vassiliev值.特别的,K′记(n+1)-平凡的纽结,#iK′记i个K′做连通和,那么K与K#(#iK′)拥有相同阶≤n的Vassiliev值. 证明 先证明如果K与L是n-相似的纽结,那么有下式成立 (1) 当n=1时,利用v(KD)=v(K+)-v(K-) 归纳,有 假设n=k-1时,定理成立.若K与L是k-相似的(关于{A1,A2,…,Ak}),则K与L是(k-1)-相似的(关于{A1,A2,…,Ak-1}),则 再反复运用关系式(1)并运用引理2即证得定理. 定理4 若K是n-平凡纽结,则当 1≤m 1≤m 证明 由式(1)有 从而vm(K)=vm(O). 对纽结不变量的研究对纽结分类意义非凡,而Vassiliev不变量特色明显,其作用不容忽视.寻找和合成拓扑新颖的蛋白质是生物学目前面临的挑战和机遇,希望借助Vassiliev不变量获得突破. [1] Barnatan D. On the Vassilliev knot invariants[J]. Topology, 1995, 34(2):423-472. [2] Ohyama Y. Vassiliev invariants and similarity of knots[J]. Proc.Amer. Math.Soc,1995,123: 287-291. [3] Stanford T. Braid commutators and Vassiliev invariants[J]. Pacific J.Math,1996,174: 269-276. [4] Yasutaka N, Ohyama Y. Knots with given finite type invariants and Conway polynomial[J]. Knot Theory Ramifications,2006, 15 (2):205-215. [5] Zhu J. On Jones knot invariants and Vassiliev invariants[J]. J.Math, 1998, 27(2) : 293-299. [6] Kofman I. Approximating Jones coefficients and other link invariants by Vassiliev invariants[J]. Journal of knot theory and its ramifications, 2000,9(7):955-966. [7] 霍承刚.纽结的Vassiliev不变量[D].大连:辽宁师范大学,2007. [8] 霍承刚.辫交换子与Vassiliev不变量[J].海南大学学报(自然科学版),2013,31(4):311-312. Vassiliev Invariant and Similarity of Knots Huo Chenggang (School of Mathematics and Statistics, Suzhou University, Suzhou 234000, China) In the report, a kind of important knot invariant, Vassiliev invariant, was introduced, and the similarity of knots was used to analyze its some important characteristics. knot; Jones polynomial; Vassiliev invariant; similarity of knots 2015-01-12 安徽省高校省级自然科学研究项目(KJ2013A248);宿州学院教研项目“应用型院校近世代数课程教学改革的探索与实践”(szxyjyxm201319);宿州学院大学生科研项目(KYLXWKB14-16) 霍承刚(1980-),男,山东禹城人,讲师,硕士,研究方向:低维拓扑,E-mail:huochenggang_2006@163.com 1004-1729(2015)03-0212-03 O ADOl:10.15886/j.cnki.hdxbzkb.2015.00392 Vassiliev 不变量与纽结的相似性


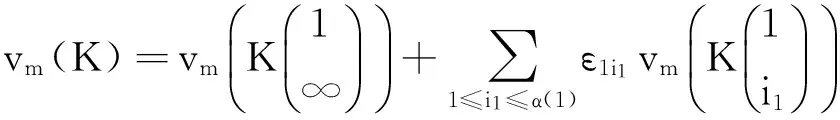



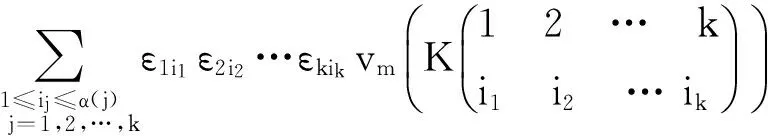






3 结束语
