一种边优先的露天煤矿DEM构建算法
2015-02-21赵景昌白润才刘光伟
赵景昌,白润才,刘 威,刘光伟
(1.辽宁工程技术大学矿业学院,辽宁阜新 123000;2.辽宁工程技术大学理学院,辽宁阜新 123000)
一种边优先的露天煤矿DEM构建算法
赵景昌1,白润才1,刘 威2,刘光伟1
(1.辽宁工程技术大学矿业学院,辽宁阜新 123000;2.辽宁工程技术大学理学院,辽宁阜新 123000)
摘 要:DEM(Digital Elevation Model,数字高程模型)是以高程为地形属性,用来描述地形表面形态属性信息的数字表达模型。根据数字化露天煤矿DEM构建需求,提出了一种边优先的DEM构建算法。该算法基于二维空间直线体素遍历原理建立边的格网索引,并采用“最小外接矩形”法搜索DT点。为了确保DEM对地形描述的正确性,采用改进的平坦区域搜索修正算法对相邻等值线之间的平坦区域进行修正。实验及应用结果表明,该算法时间效率高,运行稳定,建模精度可靠,能够满足露天煤矿DEM构建需要。
关键词:DEM;边优先;体素遍历;最小外接矩形;DT点搜索;平坦区域修正
责任编辑:许书阁
赵景昌,白润才,刘 威,等.一种边优先的露天煤矿DEM构建算法[J].煤炭学报,2015,40(8):1827-1833.doi:10.13225/ j.cnki.jccs.2014.1026
DEM(Digital Elevation Model,数字高程模型)是以高程为地形属性,用来描述地形表面形态属性信息的数字表达模型。DEM最主要的3种表示模型是:规则格网模型、等高线模型和不规则三角网(triangulated irregular network,TIN)模型[1-2]。其中,TIN通过从不规则分布的数据点生成连续三角面来逼近地形表面,与格网模型相比,TIN模型在某一特定分辨率下能用更少的空间和时间更精确地表示更加复杂的表面,因此可以认为TIN为目前进行精细地形表达最好和最常用的方法[3]。对于TIN模型,其基本要求有3点:TIN是惟一的;力求最佳的三角形几何形状,即每个三角形尽量接近等边三角形;保证最邻近的点构成三角形,即三角形的边长之和最小。在所有可能的三角网中,Delaunay三角网在地形拟合方面表现最为出色,因此常被用于TIN的生成[4]。
在数字化露天煤矿过程中,基于地质与地形勘测数据、采场与排土场测量验收数据以及规划设计数据等构建DEM为矿区时空数据库建立、生产计划编制设计、采剥工程量计算、矿区虚拟现实等综合应用的基础[5]。构建露天煤矿DEM就是对各种不同来源的建模数据进行三角剖分,在实际建模数据中,除离散点外,经常还存在大量约束边,如:建模边界、山脊线、山谷线、断层线、台阶线坡顶线与坡底线等,对含有约束边的建模数据进行三角剖分时,应保持其原有的约束关系,否则生成的DEM难以满足实际应用需要。
对含有约束边的建模数据进行Delaunay三角剖分即为约束Delaunay三角剖分[6-7]( Constrained Delaunay Triangulation,CDT)。CDT算法主要包括以下5类:分治算法、加密算法、边优先生长算法、两步法、扫描线算法[8-12]等。分治算法采用递归分块策略使算法复杂度接近线性,但由于在子块合并时需要将相邻子块两侧凸包边界采用自下而上的连接算法,涉及大量复杂的判断,使浮点数误差错误几率增大,算法稳定性较差;两步法首先对约束数据集建立非约束Delaunay三角网(初始三角网),然后嵌入约束线段,在约束域较简单情况下,算法效率很高,但当约束域存在洞、岛屿或约束边界比较复杂时,该算法在去除多余三角形方面较繁琐且不够稳定;加密算法由于加密点的存在破坏了原始数据集,且该算法前期数据处理较烦琐,使算法整体效率降低;扫描线算法首先将平面多边形域的所有顶点按扫描方式排列,然后按有序点寻找局部区域的一条边来构造新的三角形,但在实际应用过程中,为满足设定的优化标准,该算法需要进行边翻转等操作,且不适合在大量离散点存在的情况下应用;边优先生长算法以非约束Delaunay三角网生长算法为基础,在建网过程中,对约束边进行优先扩展,通常结合网格索引搜索扩展边DT点(能与扩展边构成Delaunay三角形的“第3点”),以实现快速三角剖分。
根据数字化露天煤矿对DEM构建的具体需求,结合露天煤矿DEM建模数据特点,笔者提出了一种改进的边优先CDT算法,实验与实际应用证明,该算法时间效率高,运行稳定,建模精度可靠,能够较好地满足数字化露天煤矿DEM构建的需要。
1 算法思想与数据结构
1.1 算法思想
本文算法以露天煤矿DEM建模数据中的约束边作为优先扩展对象,边界约束边向内收缩、边界内约束边向外扩展,直至所有边均饱和(除边界约束边外,边邻接三角形数2个)为止。上述过程中,扩展边DT点搜索是决定算法效率的关键因素之一,而DT点的搜索效率则取决于DT点搜索范围以及参与DT点可见性判断的边集合规模。本文算法采用分块技术,并基于二维空间直线体素遍历原理建立边的格网索引,使每条边只关联于其穿越的格网单元,大大减少了参与DT点可见性判断计算的边数,同时,采用“最小外接矩形”法,将每条扩展边DT点的初始搜索范围限定于该边最小外接矩形所覆盖的格网单元内,从而确保算法具有较高的整体效率。
在基于露天煤矿地质与地形属性等值线构建DEM时,由大量平三角形(3个顶点高程相等的三角形)构成的平坦区域会使DEM对地形与地质实体的空间形态表达失真,笔者基于DEM拓扑关系,根据平坦区域内相邻三角形所构成四边形的凸凹性,分别采用顶点插入与对角边交换法修正平坦区域,提高了DEM对地形表达的精度。
1.2 数据结构
本文算法主要数据对象包括:顶点(Vertex)、边(Edge)、Delaunay三角形(DT)、约束Delaunay三角网(CDT)、索引格网(Grid)、索引单元格(GridCell) 等,数据结构如图1所示。
2 边优先的露天煤矿DEM构建
2.1 建立点与边格网索引
建立点与边的格网索引就是将构建DEM的离散数据域划分为大小相同的单元格,然后把离散点放到其所在单元格中,把边放到其所穿越的单元格中,每个单元格分别存储位于其内部的离散点、穿越或位于该单元格内部的边,从而建立起单元格、离散点、边之间的索引关系,目的就是使不规则的DEM离散数据分布“规则化”,提高DEM构建过程中DT点的搜索效率。
索引单元格过大或过小都会增加查询次数而降低算法效率,笔者经多次实验确定合理的格网单元边长cellSize为所有约束边平均边长的1.3倍。
建立点的格网索引比较简单:设某点的平面坐标为(x0,y0),建模数据域最小外接矩形左下角点的坐标为(xmin,ymin),格网单元边长为cellSize,则该点所在索引单元格的位置(即单元格的行坐标rowId与列坐标colId)可按下式计算:
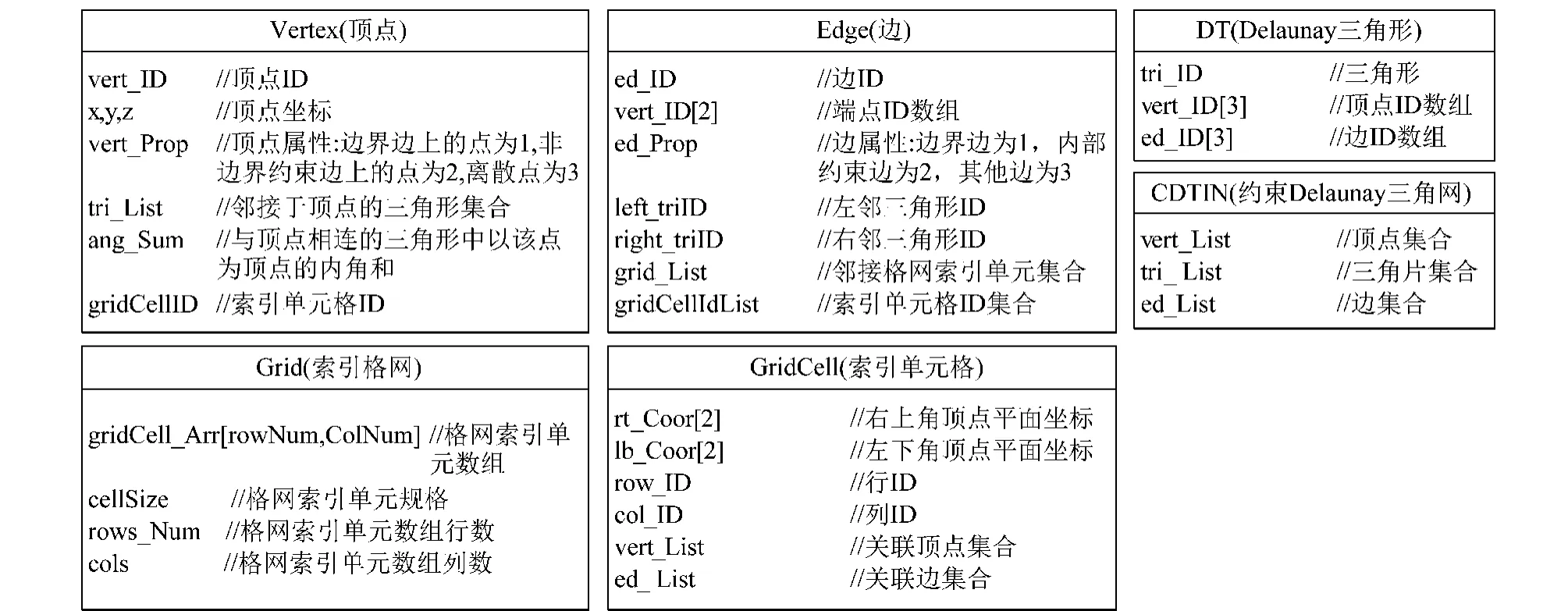
图1 本文算法主要数据结构Fig.1 Data structures of the algorithm
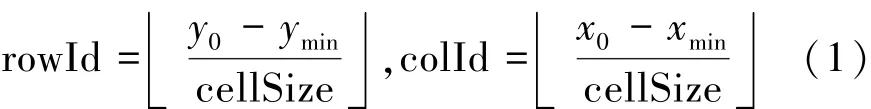
建立边的格网索引时,一种较粗略的方法是用边最小外接矩形来确定边的索引单元格,如图2(a)所示,图中虚线所示矩形是边AB的最小外接矩形,则该矩形范围内的16个单元格即为边AB的索引单元格,而边AB实际穿越的单元格仅为图2(b)中阴影所示7个单元格。
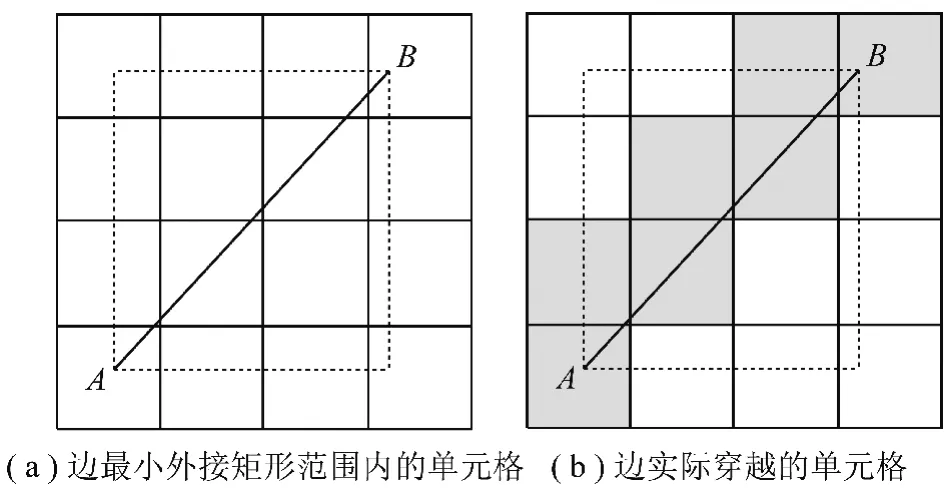
图2 边格网索引示意Fig.2 Diagram of edge grid index
可见,用边的最小外接矩形来确定边的索引单元格范围过大,在判断DT点可见性时,会因为存在大量不必要的相交检测计算而影响算法效率。为了减少DT点可见性判断时的计算量,提高算法整体效率,本文算法基于二维空间直线体素遍历原理[13]建立边的格网索引,使每条边仅与其实际穿越的单元格建立索引关系,具体步骤如下:
(1)确定主坐标轴。
设直线起点坐标为(x1,y1),终点坐标为(x2, y2),起点与终点x轴方向的距离dx= |x2-x1|,y轴方向的距离dy= |y2-y1|,若dx>dy,则x轴为主坐标轴,否则,y轴为主坐标轴(dx, dy之间存在另外7种关系,限于篇幅,本文仅以dx>dy且x2> x1,y2>y1为例,其他7种情况原理与此相同)。
(2)用式(1)确定边起点所在单元格。
(3)计算边穿越的单元格。
如图3所示,边起点V1相对其所在单元格左下角顶点沿x轴方向的距离为xs,沿y轴方向的距离为ys,边与起点单元格右侧边交点V2相对于左下角顶点的高度hy0为
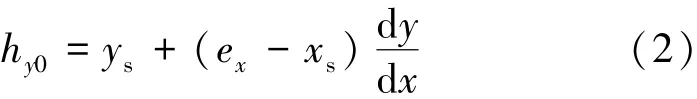

图3 计算边索引单元格示意Fig.3 Diagram of calculating the edge indexed grid cells
比较hy0与起点单元格右上角顶点P0高度ey的关系,若hy0>ey,则边穿越起点单元格的上邻单元格与右上邻单元格,否则,边穿越右邻单元格。
在到达终点之前,边与其所穿越单元格的交点坐标在x轴方向以步长递增,在y轴方向按下式累加计算:

图3中,单元格坐标用行与列ID表示,起点单元格坐标r0,c0可用式(1)计算,交点V2高度hy0用式(2)计算,起点单元格(r0,c0)右上角顶点P0高度ey,由于hy0
按上述方法计算直至边终点所在单元格,即可建立起边与其实际穿越单元格之间的索引关系。
2.2 DT点快速搜索
建立点与边格网索引的目的是为了提高DT点搜索效率,此外,DT点搜索范围也是影响DT点搜索效率的关键因素之一。陈学工等在文献[14]中提出了一种基于“最小搜索圆”的DT点搜索算法,将DT点的搜索范围控制在以当前扩展边长度1.5倍为半径的“最小搜索圆”之内,在构建有10 000个离散点的CDTIN时,算法运行时间为2.15 s。
采用“最小外接矩形”法搜索DT点,实验证明,该方法的时间效率优于“最小搜索圆”法,具体步骤如下:
(1)从边集合中取出一条非饱和边(边邻接三角形数小于2个)作为当前扩展边。
(2)用式(1)分别计算当前扩展边起点与终点单元格,并据此确定扩展边“最小外接矩形”单元格范围。
(3)在步骤(2)确定的单元格范围内搜索可用DT点,若当前扩展边为建模边界边,则根据顶点排列方向(逆时针或顺时针)搜索位于边左侧或右侧的顶点作为可用DT点;若当前扩展边不是边界边,则可同时搜索边左侧与右侧的可用DT点。
在判断点的可见性时,可按2.1节所述方法动态建立新边格网索引,并只对新边索引单元格所关联的边进行相交检测计算。
(4)计算步骤(3)所有可用DT点中与扩展边构成DT的顶角,并取顶角最大者与当前扩展边构成DT。
(5)更新顶点与边的饱和状态。点是否饱和可通过计算点角判断,点角是指与点相连的三角形中,以该点为顶点的内角和,当非边界点的点角为360°、边界点角与初始点角相等时(边界点的初始点角为与该点相连的两条边界线段的夹角),则该点饱和;边的饱和状态则根据边邻接的三角形数确定,当边邻接的三角形数为2时,则该边饱和。饱和点与边不再作为后续三角剖分中的可用DT点与扩展边,因此,将其从顶点集合与边集合中动态删除,以提高后续三角剖分效率。
(6)重复上述步骤,直至边集合为空。
2.3 局部LOP优化与平坦区域处理
一般三角剖分算法得到的TIN并不能保证是最优的,通常需要LOP优化,但对于约束Delaunay三角网CDTIN而言,由于约束边的存在,除了一般LOP优化准则外,还应遵循以下准则[15]:
(1)两个邻接三角形若不满足空圆准则应交换对角线,但如果对应对角线是约束边可不优化;
(2)若三角形的外接圆中不存在同时满足从三角形3个顶点都理想可见的顶点,则该三角形仍为DT,不需要优化。
受三角形几何特性与约束边数据特征限制,在基于地质属性等值线或地形等高线构建DEM时,会存在由大量平三角形(三角形的3个顶点属性值相等)构成的平坦区域,如图4所示。平坦区域的存在使DEM对露天煤矿地形表达失真,因此,为了获得正确的DEM,除了进行局部LOP优化外,还应对平坦区域进行修正。
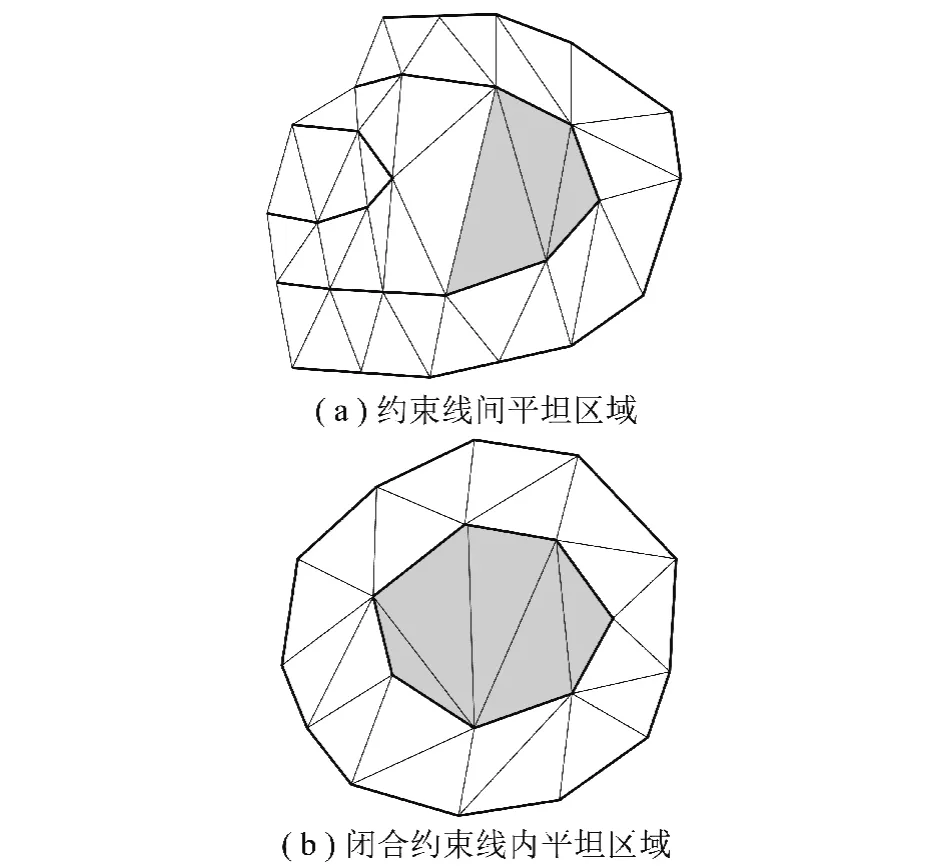
图4 平坦区域示意Fig.4 Diagram of flat region
对于露天煤矿DEM而言,在一条闭合约束线(地质属性等值线、地形等高线、台阶坡顶或坡底线)内出现平三角形的主要原因是在闭合约束线内缺少离散的特征点,如果以地形等高线或地质属性等值线为约束构建DEM,可以通过手动增加特征点来解决闭合等高线内平三角形问题;若以台阶坡顶或坡底线为约束构建露天煤矿DEM,在闭合台阶线内出现平三角形表示该闭合台阶线内高程无明显变化,可认为是对露天煤矿地形的正确描述。因此,本文只考虑对两条约束线之间的平坦区域进行修正。
平坦区域修正算法主要分为3类:数据概化修正法、特征修正法和平坦区域搜索修正法[16-18]。数据概化修正法通过减少约束线上的采样点数量并增加采样点之间的距离,从而最大限度地减少平三角形的出现,此方法损失了采样数据信息量,同时也不能完全消除平三角形;特征修正法主要是通过插入特征点、特征线消除平三角形,然而特征线的提取是一个比较复杂的问题,而且此类算法需要插入大量特征点,导致三角网重构工作量较大,修正效率较低;平坦区域搜索修正法[18]首先搜索约束线间存在的平坦区域,然后根据相邻三角形所构成四边形的凸凹性,采用插入点或交换边实现平坦区域的处理,此类算法在修正平坦区域时,在遇到内部平三角形(3条边都不是约束线的平三角形)后会出现路径二义性问题,对算法修正速度有一定影响。本文对平坦区域搜索修正法进行了改进,通过引入缓存栈,较好地解决了搜索路径二义性而导致的算法效率问题。
如图5(a)中阴影所示平坦区域(其中,tv为与平坦区域邻接的内部非平三角形;t1~t7为平三角形;t5为内部平三角形),应用本文改进的平坦区域搜索修正法进行修正的具体步骤如下:
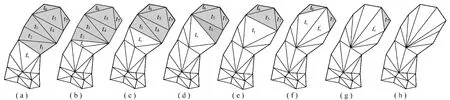
图5 平坦区域修正示意Fig.5 Diagram of flat region correcting
(1)内部非平三角形tv与平三角形t1构成凹四边形,因此,在tv与t1公共边上插入中点(该点高程用距离幂次反比法计算),将凹四边形分裂为4个三角形,修正后DEM如图5(b)所示;
(2)分裂后的4个三角形中,与t2邻接的三角形为与残留平坦区域邻接的内部非平三角形tv,tv与t2构成凸四边形,因此,交换t1与tv公共边,修正后DEM如图5(c)所示;
(3)图5(d),(e)修正方法同步骤(2);
(4)图5(e)中与tv邻接的三角形t5为内部平三角形,交换tv与t5公共边后得到两个分别与平三角形t6,t7邻接的内部非平三角形tv与tv′(存在二义性搜索路径),此时建立一个内部非平三角形缓存栈, 将tv与tv′压入缓存栈;
(5)依次弹出缓存栈栈顶三角形tv′与tv,交换tv′与t7,tv与t6公共边,结果如图5(g),(h)所示,此时平坦区域所有平三角形已全部修正,算法结束。
3 算法实验与应用实例
3.1 算法实验
本文算法已基于Visual Studio.NET平台用C#语言实现,表1所列为本文算法与文献[3,14]算法在相同实验环境(Windows 7中文旗舰版SP1操作系统,Intel(R) Core(TM) i7-2720QM CPU 2.20 GHz, 4 GB DDR3内存)下,用5组数据构建DEM的运行时间(其中第4、第5组数据是基于地形等高线的DEM数据,无离散的特征高程点)。
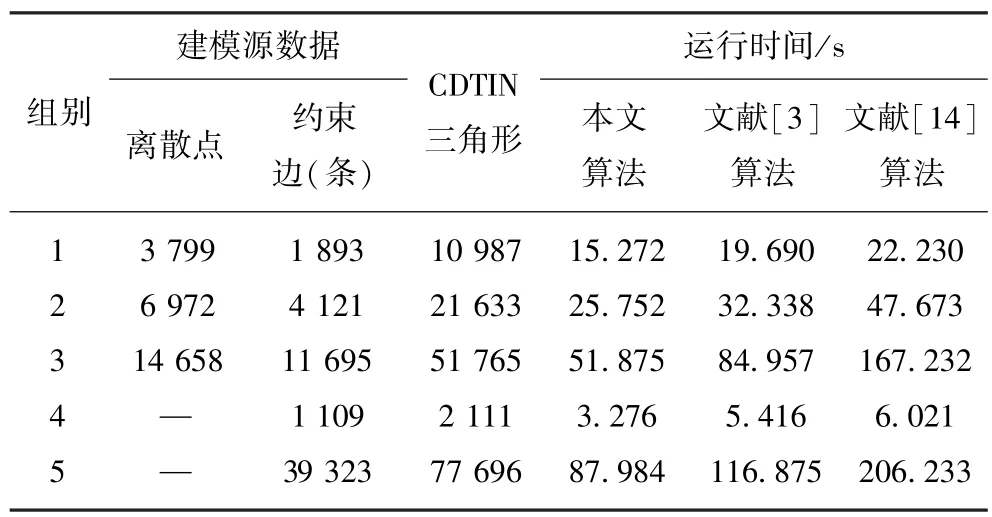
表1 算法运行时间Table 1 Running time of the algorithm
由表1中数据可知,在不同特征、不同规模的数据条件下,本文算法时间效率均高于文献[3,14]算法:其中文献[3]算法与本文算法DT点搜索范围是一致的,但在建立边格网索引时,文献[3]为根据边最小外接矩形来确定边的索引单元格范围,在后续建网过程中判断DT点相对于扩展边的可见性时,由于存在大量不必要的相交检测计算而影响了算法整体效率;文献[14]算法基于“最小搜索圆”确定DT点搜索范围,较本文“最小外接矩形”法范围大,DT点搜索时参与计算的点与边数较多、计算量较大而导致算法效率较低。
3.2 应用实例
本文算法已应用在笔者开发的露天煤矿剥采计划CAD软件系统中,图6为应用本文算法生成的地形DEM二维视图,图7为应用本文算法生成的露天煤矿现势DEM与采场计划DEM三维渲染图。
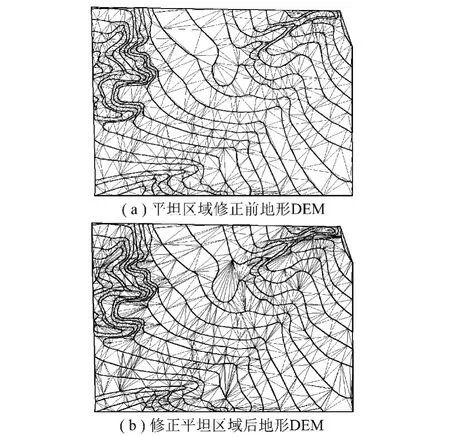
图6 地形DEM二维视图Fig.6 2D view of terrain DEM

图7 露天煤矿现势DEM与计划DEM三维渲染图Fig.7 3D rendering of open-pit coal mine’s present situation and plan DEM
实际应用表明,本文算法运行稳定,时间效率高,建模精度可靠,可广泛应用于各种数据条件下露天煤矿DEM构建。
4 结 语
DEM构建算法是数字化露天煤矿重要的基础算法之一。本文算法基于二维直线体素遍历原理建立边格网索引,并采用“最小外接矩形”法进行DT点快速搜索,此外,针对基于等值线构建DEM时存在大量平三角形而影响模型精度问题,提出了一种改进的等值线间平坦区域修正算法。实验及应用结果表明,本文算法时间效率高,运行稳定,建模精度可靠,能够满足露天煤矿DEM构建需要。
随着多核与网络时代的到来,基于多核的多线程并发编程以及分布式并行编程将是未来算法性能提升的主要途径,笔者将继续深入研究多核条件下的DEM并行构建算法,以满足海量数据露天煤矿DEM快速构建的需要。
参考文献:
[1]邬 伦,刘 瑜,张 晶,等.地理信息系统:原理、方法和应用[M].北京:科学出版社,2001:195-200.
Wu Lun,Liu Yu,Zhang Jing,et al.Geographic information system: Theory,method and application[M].Beijing:Science Press,2001: 195-200.
[2]胡金星,潘 懋,马照亭,等.高效构建Delaunay三角网数字地形模型算法研究[J].北京大学学报(自然科学版),2003, 39(5):736-741.
Hu Jinxing,Pan Mao,Ma Zhaoting,et al.Study on faster algorithm for constructing Delaunay triangulations DTM[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2003,39(5):736-741.
[3]汤国安,刘学军,闾国年.数字高程模型及地学分析的原理与方法[M].北京:科学出版社,2006:107-110.
Tang Guo’an,Liu Xuejun,Lü Guonian.Principles and methods of digital elevation model and analysis[M].Beijing:Science Press, 2006:107-110.
[4]李志林,朱 庆.数字高程模型[M].武汉:武汉测绘科技大学出版社,2000:34-35.
Li Zhilin,Zhu Qing.Digital elevation model[M].Wuhan:Wuhan Technical University of Surveying and Mapping Press,2000:34-35.
[5]隋 心,徐爱功,宋伟东.露天矿精细DEM模型的建立及更新方法[J].测绘科学,2013,38(3):148-150.
Sui Xin,Xu Aigong,Song Weidong.Establishment and update of fine DEM for strip mine[J].Science of Surveying and Mapping,2013, 38(3):148-150.
[6]刘学军,龚健雅.约束数据域的Delaunay三角剖分与修改算法[J].测绘学报,2001,30(1):83-88.
Liu Xuejun,Gong Jianya.Delaunay triangulation of constrained data set[J].Acta Geodaetica et Cartographica Sinica,2001,30(1):83-88.
[7]Floriani L D.An online algorithm for constrained Delaunay triangulation[J].Graphical Models and Image Processing,1992,54 (3): 290-300.
[8]Chew L P.Constrained Delaunay triangulations[J].Algorithmica, 1989,4(1):97-108.
[9]Boissinnat J D.Shape reconstruction from planar cross sections[J].Computer Vision,Graphics,and Image Processing,1988,44(1):1-29.
[10]Piegl L A.Algorithm and data structure for triangulation multiply connected polygonal domains[J].Computer and Graphics,1993,17(5):563-574.
[11]Sloan S W.A fast algorithm for generating constrained Delaunay triangulations[J].Computers & Structures,1993,47(3):441-450.
[12]Domiter V,žalik B.Sweep-line algorithm for constrained Delaunay triangulation[J].International Journal of Geographical Information Science,2008,22(4):449-462.
[13]刘勇奎,云 健,王晓强,等.沿三维直线的非单位体素遍历的多步整数算法[J].计算机辅助设计与图形学学报,2006, 18(6):812-818.
Liu Yongkui,Yun Jian,Wang Xiaoqiang,et al.A multi-step integer algorithm for non-unit voxel traversing along a 3D line[J].Journal of Computer-Aided Design & Computer Graphics,2006,18(6): 812-818.
[14]陈学工,马金金,黄 伟,等.一种基于最小搜索圆平面多边形域约束Delaunay三角剖分算法[J].小型微型计算机系统, 2011,32(2):374-377.
Chen Xuegong,Ma Jinjin,Huang Wei,et al.Constrained delauny triangulation algorithm for planar polygonal domains based on minimum search circle[J].Journal of Chinese Computer Systems,2011,32(2):374-377.
[15]周晓云,刘慎权.实现约束Delaunay三角剖分的健壮算法[J].计算机学报,1996,19(8):615-624.
Zhou Xiaoyun,Liu Shenquan.A robust algorithm for constrained Delaunay triangulation[J].Chinese Journal of Computers,1996, 19(8):615-624.
[16]Mark Ware J.A procedure for automatically correcting invalid flat triangles occurring in triangulated contour data[J].Computer & Geosciences,1998,24(2):141-150.
[17]陈学工,黄晶晶.基于等高线建立的TIN中平坦区域的修正算法[J].计算机应用,2007,27(7):1644-1646.
Chen Xuegong,Huang Jingjing.Corrective algorithm of flat areas occurring in TIN constructed from contours[J].Computer Applications,2007,27(7):1644-1646.
[18]解愉嘉,刘学军,胡加佩.无平三角形处理的等高线数据三角化方法[J].南京师大学报(自然科学版),2012,35(4):106-111.
Xie Yujia,Liu Xuejun,Hu Jiapei.Triangulating the contour data without flat triangle treatment[J].Journal of Nanjing Normal University (Natural Science Edition),2012,35(4):106-111.
Zhao Jingchang,Bai Runcai,Liu Wei,et al.An edge-prior DEM construction algorithm for open-pit coal mine[J].Journal of China Coal Society,2015,40(8):1827-1833.doi:10.13225/ j.cnki.jccs.2014.1026
An edge-prior DEM construction algorithm for open-pit coal mine
ZHAO Jing-chang1,BAI Run-cai1,LIU Wei2,LIU Guang-wei1
(1.School of Mining,Liaoning Technical University,Fuxin 123000,China;2.College of Science,Liaoning Technical University,Fuxin 123000,China)
Abstract:DEM(Digital Elevation Model) is a digital representation model of the terrain surface morphology property information using the elevation as the terrain property.According to the demand for DEM construction in digitalizing open-pit coal mine,an edge-prior DEM construction algorithm was put forward in this paper.The edge grid index was established based on two dimensional linear voxel traversal principle,and the“minimal circumscribed rectangle”method was adopted to search the DT point.In addition,in order to ensure the true terrain description of DEM,the flat regions between adjacent contour lines were corrected with the improved flat region searching and correcting algorithm.Test and application results show that the algorithm is of high efficiency,stable,reliable and accurate,and can meet the requirements of open-pit coal mine DEM construction.
Key words:DEM;edge-prior;voxel traversal;minimal circumscribed rectangle;DT point searching;flat region correcting
作者简介:赵景昌(1974—),男,内蒙古宁城人,讲师,博士研究生。E-mail:lntuzjc@126.com
基金项目:国家自然科学基金资助项目(51304104);辽宁省教育厅科学研究一般资助项目(L2011051)
收稿日期:2014-08-06
中图分类号:TD176
文献标志码:A
文章编号:0253-9993(2015)08-1827-07
