加筋板低周疲劳寿命和累积塑性应变模型
2015-02-21汪丹杨平邓军林董琴
汪丹,杨平,2,邓军林,董琴
1武汉理工大学交通学院,湖北武汉 430063
2武汉理工大学高性能舰船技术教育部重点实验室,湖北武汉 430063
加筋板低周疲劳寿命和累积塑性应变模型
汪丹1,杨平1,2,邓军林1,董琴1
1武汉理工大学交通学院,湖北武汉 430063
2武汉理工大学高性能舰船技术教育部重点实验室,湖北武汉 430063
为分析加筋板结构累积塑性破坏的影响,应用损伤力学基础理论,并结合筋板相互影响系数,以塑性应变为损伤演化的控制参量,推导并建立加筋板结构低周疲劳累积递增塑性应变模型和低周疲劳寿命模型。将加筋板在循环载荷下的疲劳损伤变量引入累积递增塑性应变方程中,通过积分变换,推导出循环载荷下船舶加筋板结构轴向累积塑性应变的演化方程及其低周疲劳寿命本构模型;采用船舶通用高强度402钢相关材料疲劳特性参数对船舶加筋板结构低周疲劳寿命模型进行对比分析;将塑性应变发展理论模型与有限元计算结果进行比较,分析平均应力和筋条刚度比对累积塑性应变的影响规律。结果表明,该模型较好地反映了船舶加筋板结构的轴向累积塑性应变演化规律,同时能方便地对船舶结构低周疲劳强度进行评估、校核。
损伤力学;加筋板;低周疲劳;累积塑性应变
0 引 言
研究表明,船体结构的总体破坏[1]往往是低周疲劳破坏与递增塑性破坏耦合作用的结果,而传统的船舶结构疲劳分析主要围绕高周疲劳展开而忽略了低周疲劳,直至最近频繁发生的海损事故以及船舶结构的大型化发展,才引起船舶行业对低周疲劳问题的重视。低周疲劳引起的船舶结构损伤为塑性损伤,与碰撞和触礁现象不同,疲劳损伤的影响不是瞬时的,而是随着时间不断累积,最终导致船舶结构发生塑性破坏而产生宏观裂纹,裂纹在疲劳应力作用下不断扩展直至引发船舶结构断裂。我国在塑性分析领域内的著名学者陈刚和刘应华[2]通过多年大量研究后明确指出:在较大循环载荷作用下,结构进入塑性变形,在不断累积或不断反复的过程中,最终将导致结构破坏,其破坏形式分别对应于增量塑性变形破坏(或棘轮效应)或交变塑性变形破坏(或低周疲劳)。“应变累积”是指塑性变形随循环次数的增加不断累积的行为,随着循环次数的增加,船体结构逐渐积累出现明显的大塑性应变。当船体产生的塑性变形累积值超过某一限定值后,会引发船体局部结构低周疲劳裂纹的形成、扩展并最终产生结构的总体断裂破坏。因此,本文将采用损伤力学理论和方法,推导建立适合船舶的加筋板低周疲劳损伤力学模型。为准确评估加筋板在交变载荷作用下的长期稳定性和安全性,对加筋板的循环疲劳塑性应变理论进行研究。将加筋板在循环载荷下的疲劳损伤变量方程引入累积塑性应变方程中,通过积分变换,推导出低周疲劳循环条件下加筋板轴向塑性应变的演化方程。
1 理论分析
1.1 损伤力学模型
低周疲劳破坏是一个能量耗散的过程,疲劳破坏的物理本质与损伤力学基础理论一致。由文献[3-4]可知,损伤过程是一个能量耗散过程,而耗散特性可用耗散势或损伤流动势的热力学势ψ*来描述,它是关于体积能密度Y的凸函数。由热力学的对偶关系和内变量的正交流动法则,可得

式中,D为用来描述材料的细观损伤变量。由式(1)可知,由耗散势就可以得到损伤演化方程。
为了推导损伤演化方程,参考文献[5]给出的耗散势ψ*,可表示为
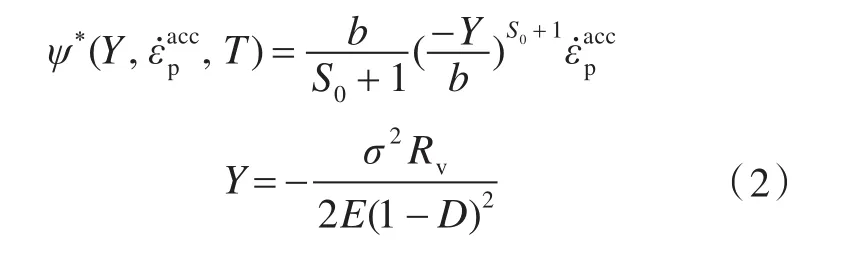
式中:Rv为三轴应力比;E为弹性模量;S0为依赖于温度的材料特性参数;b为材料常数为累积塑性应变率;σ为所受的外力。
将式(2)代入式(1),可得

由损伤力学的有效应力概念[6],可得有效应力的表达式为

将式(4)代入式(3),可得

1.2 船舶加筋板累积塑性应变模型
在对加筋板进行分析的时候,需给予必要的简化,并确定一些基本假设。基于递增塑性准则的加筋板分析方法假设如下:
1)加筋板模型被离散成一系列小的结构单元,计算时不考虑结构单元之间的相互作用;
2)材料为理想弹塑性材料。
低周疲劳一般在高上限应力、大振幅的周期加载情况下发生。根据Ramberg-Osdood应变硬化率[8],塑性应变εp与等效应力考虑损伤时表达式为

式中,K和m分别为疲劳试验确定的材料特性参数。在一维单轴应力状态下由式(6)求导可得

将式(8)代入式(3),则
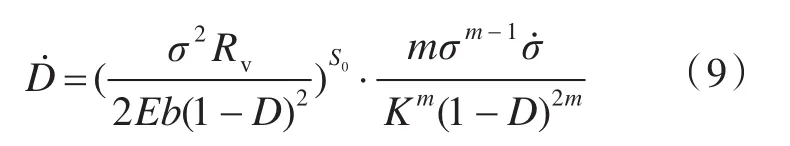
对于加筋板筋条对板强度的影响,已有学者提出用含有参数ky的解析表达式来表示加强筋对板强度的影响系数,即[9]

式中:tw为加强筋腹板厚度;t为带板厚度。对于不同的型材,d的取值不同为加筋板的长宽比),其中:
角钢d=0.98-0.14(L/W)
扁钢d=0.12-0.02(L/W)

故加强筋低周疲劳损伤力学模型为
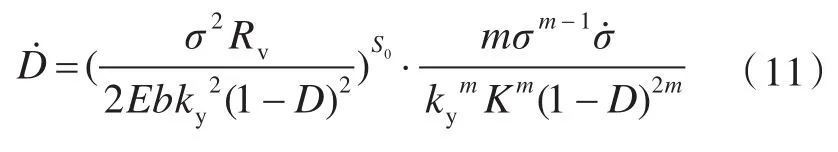
在循环载荷作用下,用平均应力σa代替单轴应力σ,则循环损伤模型由式(11)可得

设低周疲劳循环次数N=0时,结构不存在损伤,即D=0;低周疲劳破坏N=NF时,D=1,则

所以得到低周疲劳完全破坏时循环次数

由式(13)可得低周疲劳循环次数为N时,低周疲劳损伤演化方程为

将式(15)代入式(8),得
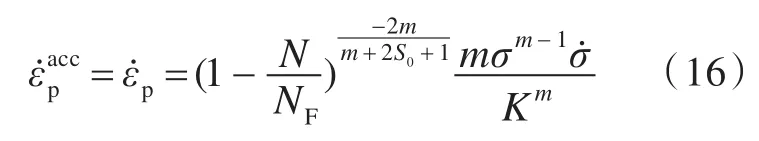
在循环载荷作用下[10],加筋板变形的弹性部分在卸载的过程中将会得到恢复,但是不可逆变形(又称塑性变形或残余变形)会残留下来。因此,一个循环周期内轴向塑性应变量等于该周期加载阶段的轴向塑性应变量。所以

对式(17)进行积分,并代入边界条件

得低周疲劳循环下船舶加筋板轴向累积塑性应变模型为

其中:ε0为初始塑性应变;εF为循环结束时船舶加筋板结构达到累积塑性破坏状态下的轴向塑性应变。
从实验观测可知损伤对于应变的演变过程是线性的[11],故可取S0=1;另外,在单轴应力状态下,三轴应力比Rv=1,b=1,则式(14)、式(19)可分别简化为:

式(20)、式(21)即分别为基于损伤力学的船舶加筋板单轴载荷下的低周疲劳寿命模型和累积塑性应变模型。
2 有限元模型建立
本文选取在均匀拉伸载荷作用下,具有缺口的船体加筋板有限元模型进行计算,模型几何图与加载历程示意图如图1所示。图中:加筋板宽度W=200 mm,长度L=300 mm;缺口半径r= 3 mm;板厚t=3 mm;σ为单向拉伸循环外载荷,边界条件为加筋板左侧Ux=0,加筋板下端Uy=0。单元类型选用Plane 182单元和Beam 189单元,材料本构关系模型选用Chaboche非线性强化准则。

图1 模型几何图与加载历程示意图Fig.1 A notched stiffener plate and loading history
带缺口的船体板平面图及其有限元计算网格模型如图2所示。为降低单元网格划分对缺口根部应力应变的影响,在缺口局部区域进行网格细化处理,随着网格的细化,计算结果趋于稳定。

图2 缺口加筋板有限元网格划分模型Fig.2 Finite element mesh model of the notched stiffener plate
在循环拉伸载荷作用下,带缺口的船体加筋板构件通过ANSYS自带的Chaboche非线性随动强化模型进行数值分析,Chaboche模型参数选取如表1所示(表中,C1~C6为材料参数)。模型参数的选取根据文献[12]的实验结果,采用单一变量法调整各个模型参数,直至模拟曲线与实验曲线基本吻合而最终确定[13],该本构模型能描述材料的棘轮效应。

表1 Chaboche模型材料参数Tab.1 Material parameters of Chaboche model
本文选取船舶通用高强度钢402为研究对象,其相应的材料特性参数如表2所示[14],其中σs为极限屈服强度。

表2 402钢材料特性参数Tab.2 Material parameters of 402 steel
选取缺口根部进行受力分析,在外加载荷为σmax=800 MPa,σmin=40 MPa时,其缺口根部处拉伸应力循环载荷作用下的应力应变迟滞回线如图3所示。从图中可以看出,在非对称应力循环载荷作用下,带缺口船体板构件产生了塑性应变的累积。在初始循环中,累积递增塑性应变增长较快,随着循环数的增加,累积递增塑性应变率逐渐下降,并逐渐趋于稳定。

图3 加筋板循环应力应变曲线Fig.3 The stress-strain curve based on Chaboche models
3 累积塑性应变模型分析
3.1 低周疲劳寿命比较
船舶加筋板在不同平均应力幅下,由式(20)和有限元模拟求得的相应低周疲劳寿命如图4所示。从图中可以看出,当低周疲劳寿命低于5 000次时,低周疲劳寿命模型式(20)的计算结果与有限元计算结果吻合;当402钢的低周疲劳寿命大于5 000次后,弹性应变对疲劳寿命的影响变得显著,式(20)的估算结果偏大。可见,式(20)较适用于以塑性应变为主的船舶结构低周疲劳强度的评估。

图4 不同平均应力幅下疲劳寿命对比Fig.4 Low cycle fatigue life of stiffened plate under differentσa
3.2 低周疲劳累积递增塑性应变模型对比
3.2.1 筋条刚度比对累积塑性应变的影响
讨论筋条刚度比对缺口船体加筋板构件累积塑性应变的影响,保持其循环加载载荷不变,取σmax=800 MPa,σmin=40 MPa,加筋板刚度比β= 0.1,0.2,0.3。针对图2给出的带缺口船体加筋板构件模型进行循环计算,可得出加筋板在不同刚度比下缺口顶点处的累积递增塑性应变的变化关系,如图5所示。

图5 加筋板筋条刚度比对累积塑性应变的影响Fig.5 The relationship of stiffened plate between accumulative plastic strains and number of cycles under differentβ
由图5可知,在相同的加载情况下,随着加筋板刚度比变大,缺口顶点处的累积塑性应变值变小,光板的累积塑性应变值较加筋板的要大。累积塑性应变开始增长较快,但随着循环周次的逐渐增加,最终趋于稳定。图5表明筋条刚度比对缺口船体加筋板构件累积递增塑性应变的影响明显。
3.2.2 平均应力对累积塑性应变的影响
为研究平均应力对缺口船体加筋板构件累积塑性应变的影响,分别给予其循环加载为540±100,640±100和740±100 MPa,加筋板刚度比β=0.3。选取图2所示模型进行循环计算,得出加筋板在不同平均应力下缺口顶点处的累积递增塑性应变的变化关系,如图6所示。
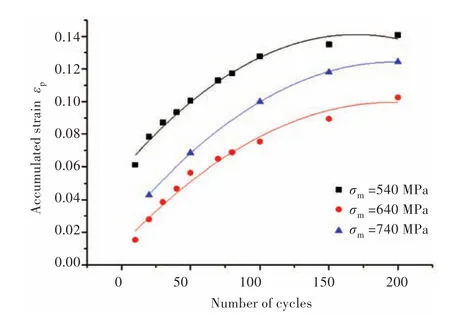
图6 平均应力对加筋板累积塑性应变的影响Fig.6 The relationship of stiffened plate between accumulative plastic strains and number of cycles under differentσm
由图6可知,随着平均应力变大,缺口加筋板顶点处的累积塑性应变值也变大,累积塑性应变开始增长较快,但随着循环周次的逐渐增加最终趋于稳定。图6表明,平均应力对缺口船体加筋板构件累积递增塑性应变的影响非常重要。
3.2.3 低周疲劳累积递增塑性应变模型对比
为对上述累积递增塑性应变模型进行验证,将有限元计算结果与根据本文中式(21)得到的拟合曲线结果进行了对比,如图7所示。根据图7中有限元计算结果和本文拟合曲线的对比可以看出,大部分曲线的相关度很好,所以该模型可以对循环载荷作用下加筋板的单轴低周疲劳累积塑性应变发展规律进行较好的反映;另外,从图7可以看出,加筋板轴向塑性应变的累积发展过程经历了从“加速”到“平稳”的过程。
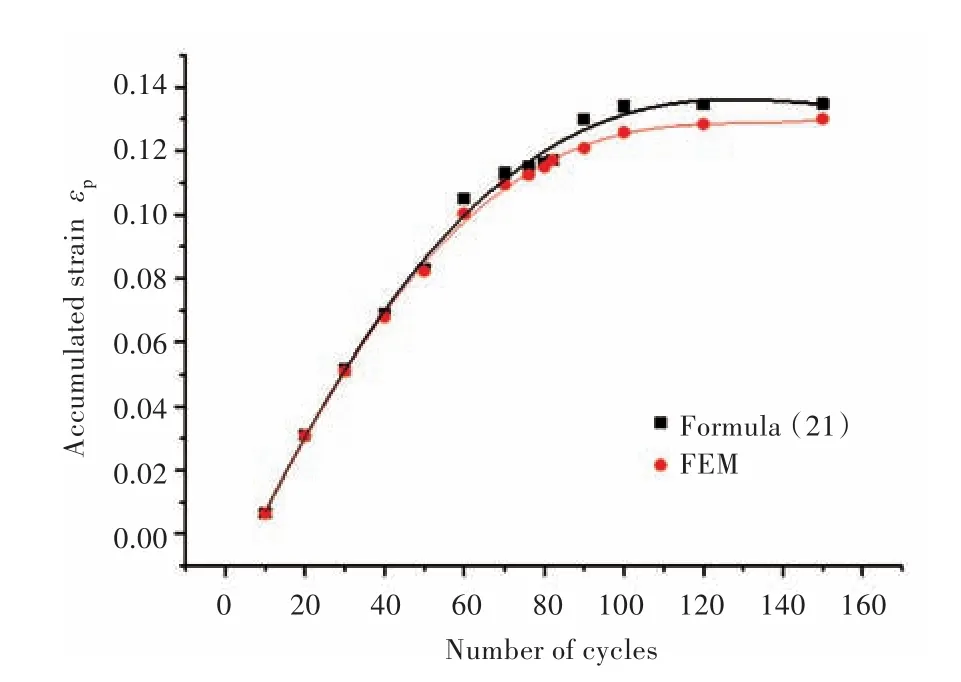
图7 累积塑性应变理论模型与有限元结果比较Fig.7 Comparison between theory model and finite element results
4 结 论
通过本文的研究,可得出以下2点结论:
1)为研究加筋板在循环载荷下轴向塑性应变的发展演化规律,在众学者工作的基础上,利用损伤力学理论,引入加强筋对板的系数推导了循环载荷下加筋板轴向塑性应变发展演化模型,经与有限元计算结果对比,发现该模型可以较好地反映单轴循环载荷下加筋板的轴向塑性应变发展演化规律。
2)此模型仅适用于一维单向加载或比例加载情况,累积塑性应变随着循环周次的增加,是先快速增加而后趋于稳定。在相同的加载情况下,随着加筋板刚度比的增加,累积塑性应变减小;平均应力增加,累积塑性应变增加。
[1] 韩芸,崔维成,黄小平,等.大型船舶结构的疲劳强度校核方法[J].中国造船,2007,48(2):60-67. HAN Yun,CUI Weicheng,HUANG Xiaoping,et al. Fatigue strength assessment of large-scale ship struc⁃tures[J].Shipbuilding of China,2007,48(2):60-67.
[2] 陈刚,刘应华.结构塑性极限与安定分析理论及工程方法[M].北京:科学出版社,2006.
[3] LEMAITRE J.A Course on damage mechanics[M]. Berlin:Springer-Verlag,1996.
[4] CHABOCHE J L,LESNE P M.A non-linear continu⁃ous fatigue damage model[J].Fatigue&Fracture of Engineering Materials&Structures,1988,11(1):1-17.
[5] CHANDRAKANTH S,PANDEY P C.An isotropic damage model for ductile material[J].Engineering Fracture Mechanics,1995,50(4):457-465.
[6] YANG X H,LI N,JIN Z H,et al.A continuous low cycle fatigue damage model and its application in engi⁃neering materials[J].International Journal of Fatigue,1997,19(10):687-692.
[7] 郑战光,蔡敢为,李兆军,等.基于损伤力学阐释Manson-Coffin低周疲劳模型[J].中国机械工程,2011,22(7):812-814. ZHENG Zhanguang,CAI Ganwei,LI Zhaojun,et al. Interpretation of Manson-Coffin model of low cycle fa⁃tigue based on damage mechanics[J].China Mechani⁃cal Engineering,2011,22(7):812-814.
[8] 娄志文.损伤力学基础[M].西安:西安交通大学出版社,1991:4-47.
[9] FUJIKUBO M,HARADA M,YAO T,et al.Estima⁃tion of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure part 2:continuous stiffened panel[J].Marine Struc⁃tures,2005,18(5-6):411-427.
[10] 许宏发,王武,方秦,等.循环荷载下岩石塑性应变演化模型[J].解放军理工大学报(自然科学版),2012,13(3):282-286. XU Hongfa,WANG Wu,FANG Qin,et al.Evolu⁃tion model of rock plastic strain under cyclic loading[J].Journal of PLA University of Science and Tech⁃nology(Natural Science Edition),2012,13(3):282-286.
[11] 李兆霞.损伤力学及其应用[M].北京:科学出版社,2002:,16-31.
[12] 王晓天,黄小平,耿峰,等.高强度材料402钢的低周疲劳性能实验研究[J].哈尔滨工程大学学报,2000,21(3):75-77. WANG Xiaotian,HUANG Xiaoping,GENG Feng,et al.Experiment of low cycle fatigue of high strength material 402[J].Journal of Harbin Engineering Uni⁃versity,2000,21(3):75-77.
[13] 苏莹.铜圆棒缺口试件拉压循环下的疲劳问题研究—模拟与实验分析[D].南宁:广西大学,2014. SU Ying.Research on fatigue problem of copper rod notched under tension and compression cycle:simula⁃tion and experimental analysis[D]. Nanning:Guangxi University,2014.
[14] 田雨,纪卓尚.船舶结构低周疲劳强度分析方法[J].哈尔滨工程大学学报,2011,32(2):153-158. TIAN Yu,JI Zhuoshang.A low-cycle-fatigue assess⁃ment method of ship structures[J].Journal of Harbin Engineering University,2011,32(2):153-158.
[责任编辑:田甜]
The low-cycle fatigue life model and the accumulative plastic strain model for stiffened plates under cyclic loading
WANG Dan1,YANG Ping1,2,DENG Junlin1,DONG Qin1
School of Transportation,Wuhan University of Technology,Wuhan 430063,China Key Laboratory of High Performance Ship Technology of Ministry of Education,Wuhan University of Technology,Wuhan 430063,China
In order to analyze the increasing accumulative plastic damage of ship stiffened plates,this pa⁃per combines the interaction coefficients of stiffeners and plates,and with plastic strain of damage evolu⁃tion being the control parameter,the low-cycle fatigue accumulative increasing plastic damage model and low-cycle fatigue life model for stiffened plates have been derived based on the theory of damage mechan⁃ics.The fatigue damage variable of the stiffened plate under cyclic loading is then introduced into the accu⁃mulative plastic strain equation.Next,by means of integral transformation,the evolution equation of axial accumulative plastic strain and the constitutive model for low-cycle fatigue life are deduced under low cy⁃clic loading.The general high strength steel 402 is adopted,with its related material fatigue characteristic parameters introduced to be compared with the low-cycle fatigue life model of stiffened plates.The theoreti⁃cal evolution results from the presented models of the accumulative plastic strain damage are compared with finite element modeling results,and the influences of mean stress and rib stiffness ratio on the accumu⁃lated plastic strain are discussed.The results indicate that the established model well reflects the evolution⁃al law of the axial plastic strain of the stiffened plate under cyclic loading and brings convenience into the evaluation of low-cycle fatigue strength of ship structures.
damage mechanics;stiffened plates;low-cycle fatigue;accumulative plastic strain
U661.41
A
10.3969/j.issn.1673-3185.2015.06.007
http://www.cnki.net/kcms/detail/42.1755.TJ.20151110.1025.014.html期刊网址:www.ship-research.com
汪丹,杨平,邓军林,等.加筋板低周疲劳寿命和累积塑性应变模型[J].中国舰船研究,2015,10(6):39-44. WANG Dan,YANG Ping,DENG Junlin,et al.The low-cycle fatigue life model and the accumulative plastic strain model for stiffened plates under cyclic loading[J].Chinese Journal of Ship Research,2015,10(6):39-44.
2015-03-18 < class="emphasis_bold"> 网络出版时间:
时间:2015-11-10 10:25
国家自然科学基金面上项目(51479153);中央高校基本科研业务费专项资金资助项目(2015-yb-004)
汪丹,女,1990年生,硕士生。研究方向:结构疲劳与断裂。E-mail:wdan27@163.com杨平(通信作者),男,1955年生,博士,教授,博士生导师。研究方向:结构疲劳与断裂。E-mail:pyang@whut.edu.cn
