乘积度量空间中两对自映象的公共不动点定理
2015-02-20郑慧慧
郑慧慧,谷 峰
(杭州师范大学理学院,浙江 杭州310036)
乘积度量空间中两对自映象的公共不动点定理
郑慧慧,谷峰
(杭州师范大学理学院,浙江 杭州310036)
摘要:在乘积度量空间中,利用自映象对的弱交换条件,证明了两对自映象的几个新的公共不动点定理,并且提供了一个支持新结果的实际例子. 所得结果改进和推广了Ozavsar和Cevikel的相关结果.
关键词:乘积度量空间;弱交换映象;公共不动点
1引言和预备知识
近年来,在不同压缩条件下映象的公共不动点理论已经取得了许多重要的研究成果.谷峰等[1]在完备度量空间中证明了弱交换映象对的公共不动点定理.Ozavsar等[2]首次引进了乘积度量空间的概念,并在完备乘积度量空间中证明了映象的一些公共不动点定理.后来He等[3]证明了乘积度量空间中弱交换映象的公共不动点定理.本文的目的是在完备乘积度量空间中讨论两对弱交换映象的公共不动点问题,证明了几个新的公共不动点定理.
定义1[2]设X是非空集合,称映象d:X×X→R+是X上的一个乘积度量,如果以下条件被满足:
1)d(x,y)≥1,∀x,y∈X,d(x,y)=1当且仅当x=y;
2)d(x,y)=d(y,x),∀x,y∈X;
3)d(x,y)≤d(x,z)·d(z,y),∀x,y,z∈X.
称(X,d)为一个乘积度量空间.
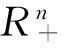
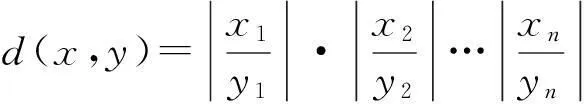

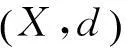
定义4[2]称乘积度量空间X是完备的,如果其中的任意积性柯西列都积性收敛于X中的某一点.
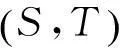
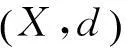
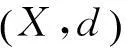
2主要结果
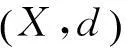
(Ⅰ)SX⊂BX,TX⊂AX;
(Ⅱ)A和S弱交换,B和T也是弱交换的;
(Ⅲ)S,T,A和B之一连续;

则S,T,A和B在X中有唯一的公共不动点.

使用条件(Ⅳ)可得
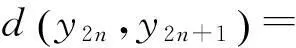
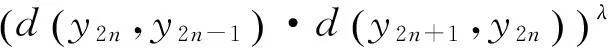
同理有
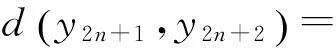

综上,∀n∈N,我们有

于是,对∀n>m,有


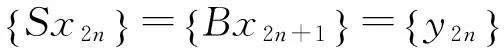


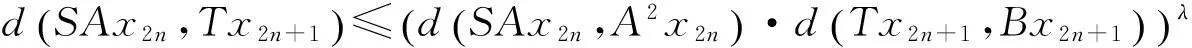
令n→∞,得
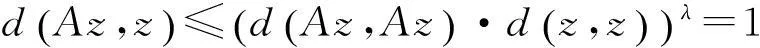
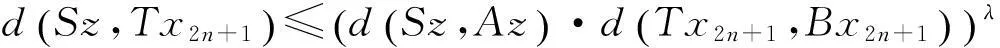
令n→∞,得

又因为z=Sz∈SX⊂BX,所以∃z*∈X使得z=Bz*. 由条件(Ⅳ)有
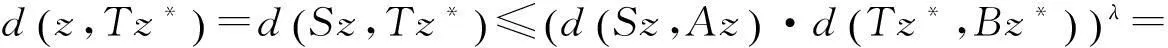
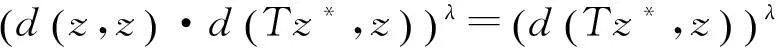
由B和T是弱交换映象可知
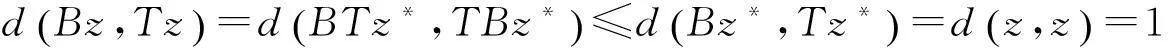
所以Bz=Tz. 进而
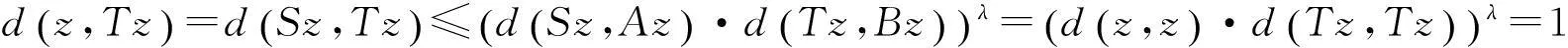
综上得Sz=Az=Bz=Tz=z,于是z是S,T,A和B的一个公共不动点.
情况2假设B是连续的,同情况1类似可得同样的结论.
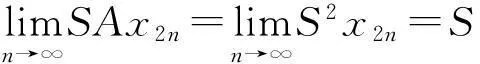

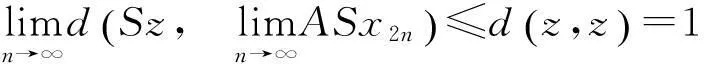

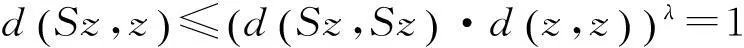
又因为z=Sz∈SX⊂BX,所以∃z*∈X使得z=Bz*. 利用条件(Ⅳ)有

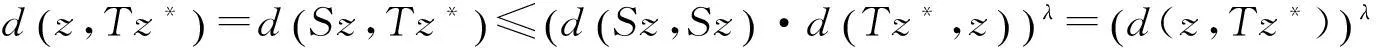
由B和T是弱交换映象可知
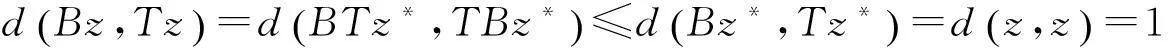
所以Bz=Tz. 由条件(Ⅳ)有
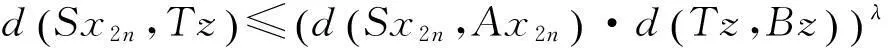
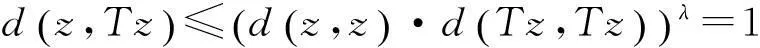
又因为z=Tz∈TX⊂AX,所以∃z**∈X使得z=Az**.由条件(Ⅳ)有

由S和A是弱交换映象可知

所以Az=Sz.
综上,我们得到Sz=Tz=Az=Bz=z,故z是S,T,A和B的公共不动点.
情况4 假设T是连续的,同情况3类似可得同样的结果.
最后,我们证明S,T,A和B有唯一公共不动点. 事实上,若w∈X也是S,T,A和B的一个公共不动点,则由条件(Ⅳ)有

注1文献[4]中定理3.5是定理1中S=T,A=B=I(I表恒等映象)时的特殊情况.
定理2设S,T,A和B是完备乘积度量空间X中的自映象,并满足下列条件:
(Ⅰ)SX⊂BX,TX⊂AX;
(Ⅱ)A和S弱交换,B和T也是弱交换的;
(Ⅲ)S,T,A和B之一连续;
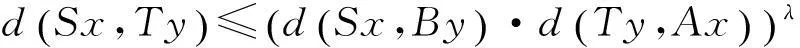
则S,T,A和B在X中有唯一的公共不动点.



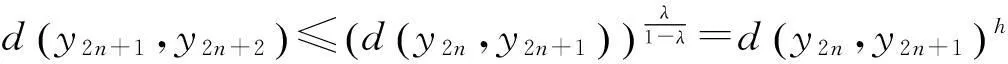
综上,∀n∈N,我们有.对n>m有
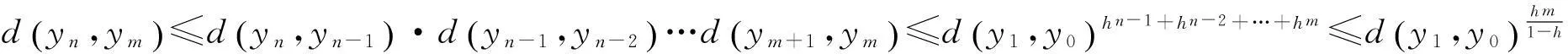
后半部分的证明与定理1类似,此处略去.
注2文献[4]中定理3.6是定理1中S=T,A=B=I(I表恒等映象)时的特殊情况.
定理3设S,T,A和B是完备乘积度量空间X中的自映象,并满足下列条件:
(Ⅰ)SX⊂BX,TX⊂AX;
(Ⅱ)A和S交换,B和T也是交换的;
(Ⅲ)S,T,A和B是连续的;
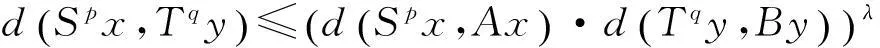
证明因为
SpX⊂Sp-1X⊂…⊂S2X⊂SX⊂BX,
TqX⊂Tq-1X⊂…⊂T2X⊂TX⊂AX.
由于A和S是交换映象,所以

同理,由于B和T是交换映象,所以
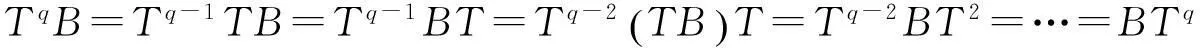
故SpA=ASp,TqB=BTq.
由于交换映象一定是弱交换映象,所以Sp,A和Tq,B都是弱交换映象对.据定理1可知,Sp,A,Tq和B有唯一公共不动点z.
下面证明S,T,A和B在X中有唯一的公共不动点.事实上,因为Spz=Az=Tqz=Bz=z,所以

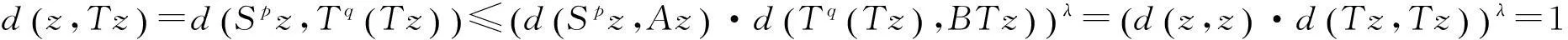
综上我们得到Sz=Tz=Az=Bz=z,所以z是S,T,A和B的公共不动点.
最后,证明S,T,A和B有唯一公共不动点.事实上,若w∈X也是S,T,A和B的一个公共不动点,则

定理4设S,T,A和B是完备乘积度量空间X中的自映象,且满足以下条件:
(Ⅰ)SX⊂BX,TX⊂AX;
(Ⅱ)A和S交换,B和T也是交换的;
(Ⅲ)S,T,A和B是连续的;
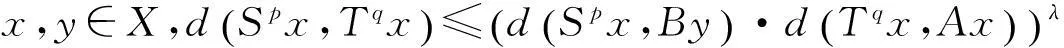
证明同定理3的证明可得Sp,A,Tq和B有唯一公共不动点z.下面证明S,T,A和B在X中有唯一的公共不动点.事实上

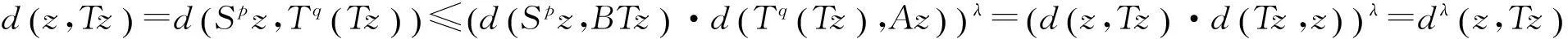
综上得到Sz=Tz=Az=Bz=z,所以z是S,T,A和B的公共不动点.
利用条件(Ⅳ)容易证得S,T,A和B的公共不动点是唯一的.
注3定理3和定理4是新结果,之前未见报道.
参考文献:
[1] 谷峰,崔丽敏,吴艳辉.几个新的压缩型映象的公共不动点定理[J].齐齐哈尔大学学报:自然科学版,2003,19(1):85-89.
[2] Bashirov A E, Kurplnara E M, OzyapIcI A. Multiplicative calculus and its applications[J]. J Math Anal Appl,2008,337(1):36-48.
[3] He X, Song M, Chen D. Common fixed points for weak commutative mappings on a multiplicative metric space[J]. Fixed Point Theory and Application,2014,2014:48.
[4] Ozavsar M, Cevikel A C. Fixed point of multiplicative contraction mappings on multiplicative metric space[EB/OL].(2012-05-23) [2014-02-08]. http://arxiv.org/pdf/1205.5131.pdf.

第14卷第4期2015年7月杭州师范大学学报(自然科学版)JournalofHangzhouNormalUniversity(NaturalScienceEdition)Vol.14No.4Jul.2015
Common Fixed Point Theorems for Two Pairs of Self-mappings
in Multiplicative Metric Space
ZHENG Huihui, GU Feng
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
Abstract:By using the weakly commutative conditions for self-mapping pairs in multiplicative metric space, this paper proves some new common fixed point theorems for two pairs of self-mapings. An example is provided to support the new results, which generalize and extend the relevant results of Ozavsar and Cevikel.
Key words:multiplicative metric space; weakly commutative mappings; common fixed point
doi:10.3969/j.issn.1674-232X.2015.04.018
通信作者:吴晓红(1976—),女,副教授,硕士,主要从事应用数学与数学教育研究.E-mail: zjvccwxh@126.com
基金项目:浙江商业职业技术学院重点科研项目(SZYZD201403).
收稿日期:2014-11-23
文章编号:1674-232X(2015)04-0428-05
中图分类号:O177.91MSC2010: 47H10;54H25
文献标志码:A
