Hopf群余代数的广义Ore扩张

胡希能, 李文强, 李金其

(浙江师范大学数理与信息工程学院, 浙江 金华 321004)

Hopf群余代数的广义Ore扩张

胡希能, 李文强, 李金其

(浙江师范大学数理与信息工程学院, 浙江 金华 321004)

摘要：把Hopf群余代数Ore扩张推广到Hopf 群余代数广义Ore扩张, 并给出了Hopf群余代数的广义Ore扩张成为Hopf 群余代数的充要条件.

关键词：Hopf群余代数;广义Ore扩张;特征

A.N.Panov在文[1]中证明了Hopf代数的Ore扩张成为Hopf代数的充要条件.Wang Zhen在文[2]中证明了Hopf代数的广义Ore扩张成为Hopf代数的充要条件.Wang Dingguo等在文[3]中把Hopf代数Ore扩张推广到Hopf群代数中, 并且给出了Hopf群代数Ore扩张成为Hopf群代数的充要条件. 论文讨论了广义Ore扩张推广到Hopf 群代数中的情形, 并且给出了Hopf群代数的广义Ore扩张成为Hopf群代数的充要条件.

设A是K-代数,τ是A的代数自同态,δ是A的τ-导子.

A的Ore扩张R=A[z;τ,δ]为K-代数,R由变量z和A代数生成, 并对任意a∈A, 满足:

za=τ(a)z+δ(a).

(1)

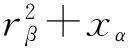
(2)

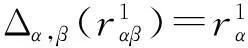
(a)xα=0或yα=0. 或

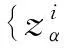
(Δα,β⊗idAγ)Δαβ,γ(zαβγ)=

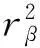
(idAα⊗Δβ,γ)Δα,βγ(zαβγ)=

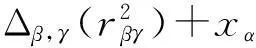
由(Δα,β⊗idAγ)Δαβ,γ=(idAα⊗Δβ,γ)Δα,βγ可得：

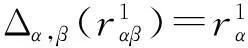
(3)

(4)

(a)当xα=0或yα=0, 结论成立.

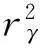
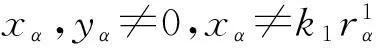
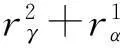
故,uα,β⊗yγ=xα⊗wβ,γ.

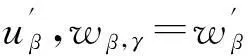
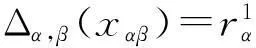
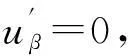
用(Δα,β⊗idAγ)Δαβ,γ=(idAα⊗Δβ,γ)Δα,βγ作用于xαβγ得:

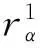
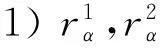
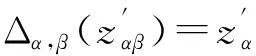
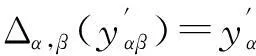
下文中, 我们假定Hopf群余代数广义Ore扩张中的元素{zα}α∈π总是满足:

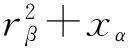
注:当xα⊗yα=0时, Hopf群代数的广义Ore扩张就是Hopf 群代数的Ore 扩张.

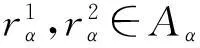
(5)

(6)

(7)

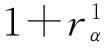
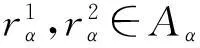
1) 存在特征χ:A1→K, 使得

(8)

2) 下列等式成立:

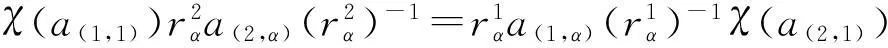
(9)

3)τα-导子δα满足:

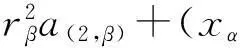
(10)

证明1)必要性. 对任意a∈Aαβ,

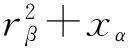
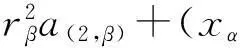
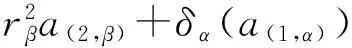
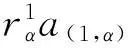
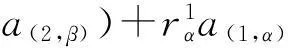
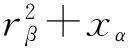
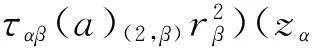
(ταβ(a)(1,α)⊗ταβ(a)(2,β))(xα⊗yβ)+Δα,βδαβ(a),

因此, Δ保持zαa=τα(a)zα+δα(a) 当且仅当下列关系成立:

(11)

(12)

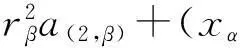
(13)

等式(13)就是等式(10).

定义一族线性映射{χα:A1→Aα}α∈π, 对任意a∈A1,

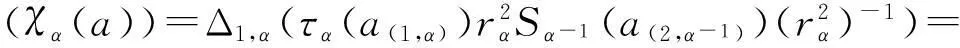
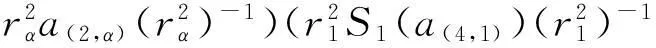
χα(a)=(ε1⊗idα)Δ1,α(χα(a))=(ε1⊗idα)(χ1(a)⊗1α)=

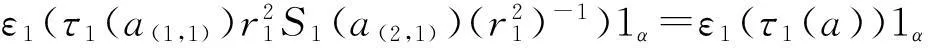
故χα可诱导出同态χ:A1→K,χ(a) =ε1(τ1(a)). 容易验证χ(ab)=χ(a)χ(b) ,χ(a+b)=χ(a)+χ(b), 因而χ是A的特征.

对任意a∈Aα,

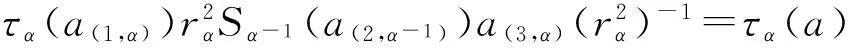
因此, 等式(8)成立.在等式(12)中取β=1得:

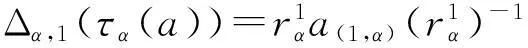
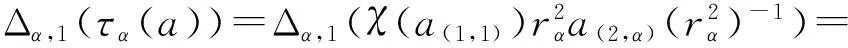
2)充分性. 证明可分为3个步骤:

第一步: 余乘法Δ={Δα}可以通过条件提升到R上并使得zαa=τα(a)zα+δα(a)成立.

因此,等式(11),(12)成立, 所以Δα,β(zαβ)Δα,β(a)=Δα,βταβ(a)Δα,β(zαβ)+Δα,βδαβ(a).

第二步：余单位可以推广到R1当且仅当ε1(δ1(a1))=0, 其中a∈A1.

等式(13)中取α=1,β=1得

两边用m(1⊗ε1)作用得

故a(1,1)ε1(δ1(a(2,1)))=0,ε1(a(1,1))ε1(δ1(a(2,1)))=ε1(δ1(a))=0.

第三步:要证对任意的a∈Aα,Sα(a)Sα(zα)=Sα(zα)Sατα(a)+Sαδα(a).由于ε1(a)=a(1,α)Sα-1(a(2,α-1)), 两边用δ1作用得

δα(a(1,α))Sα-1(a(2,α-1))+τα(a(1,α))δαSα-1(a(2,α-1))=0.

由等式(13)得

Δα-1,ατ1(a)(xα-1⊗yα)+Δα-1,αδ1(a)=

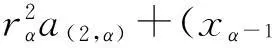
两边用m(1α-1⊗Sα)作用得

一方面,

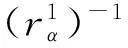
另一方面,

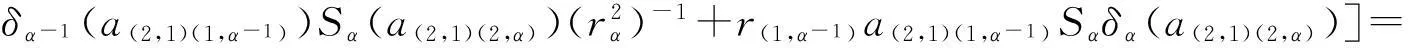
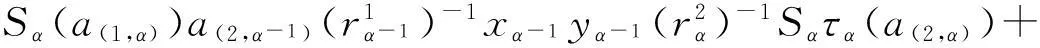
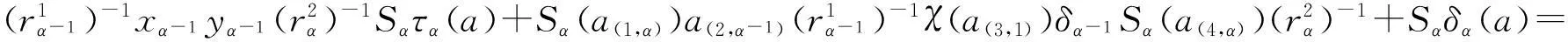
由上面的准备可得

Sα(zα)Sατα(a)+Sαδα(a)=

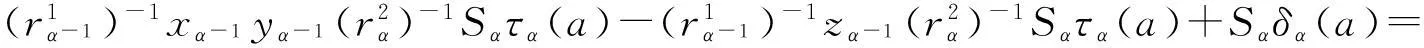
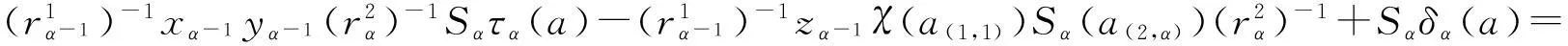
参考文献:

[1] Panov A N. Ore extensions of Hopf algebras[J]. Mathematical Notes,2003, 74: 401-410.

[2] Wang Z. Generalized Hopf-Ore extensions[J].(2013-12-01) [2014-01-05]. http://arxiv.org/abs/1312.0178.

[3] Wang D G, Lu D W. Ore extensions of Hopf group coalgebras[J]. Journal of the Korean Mathematical Society, 2014, 51(2):325-344.

Generalized Ore Extensions of Hopf Group Coalgebras

HU Xineng, LI Wenqiang, LI Jinqi

(College of Mathematics, Science and Information Engineering, Zhejiang Normal University, Jinhua 321004, China)

Abstract:The Ore extension of Hopf group coalgebras is extended to the generalized Ore extension of Hopf group coalgebras. And the necessary and sufficient condition for the generalized Ore extension of Hopf group coalgebras to become Hopf group coalgebras is given.

Key words:Hopf group coalgebras; generalized Ore extensions; character

文章编号:1674-232X(2015)04-0423-05

中图分类号:O153.3MSC2010: 16T99

文献标志码:A