变结构控制课堂教学中动力系统切换面设计
2015-02-20姚合军
姚合军
(安阳师范学院 数学与统计学院,河南 安阳 455000)
变结构控制课堂教学中动力系统切换面设计
姚合军
(安阳师范学院 数学与统计学院,河南 安阳 455000)
[摘要]研究了相变量系统和多输入多输出动力系统切换面的六种设计方法。基于Hurwitz稳定性判据和等效控制、极点配置、最优控制、特征向量任置法,给出了多输入多输出动力系统的切换面设计方法,保证滑模面的稳定,为变结构控制器设计做好铺垫。
[关键词]变结构控制;切换面;动力系统
1引言
基于不连续控制率的变结构控制方法是处理系统鲁棒稳定性的有效方法[1-4]。众所周知,设计变结构控制器有两个重要的环节: 1.设计合适的变结构控制器使得系统状态在有限时间内到达并保持在切换面上。2.设计恰当的切换面和控制器保证被转移到切换面上的点始终在切换面上运动,并渐近趋于原点。针对环节1,已有大量的研究结果报道,得到了各种各样的趋近率保证系统状态在有限时间内到达切换面。文献[5]设计了带有死区输入的线性系统的变结构控制器[6]。Niu等人研究了针对一类具有非匹配不确定性和状态及输入时滞系统,设计了系统的变结构控制器。文献[7]中,Xia等人研究了具有时变输入和状态时滞的线性系统的变结构控制问题。以线性矩阵不等式形式给出了切换面设计的时滞依赖的充分条件。Liu等人利用全局变结构控制方法研究了一类非线性系统的镇定问题,得到了一个新的鲁棒控制器,改进了系统的鲁棒性和稳定性[8]。
然而控制器设计的前提是切换面的设计。近年来,有关于切换面设计的结果也有不少的报道。文献[9]研究了一类多输入多输出系统的变结构控制问题,利用极点配置法设计切换面,并采用一种改进的指数趋近律,有效降低变结构所产生的抖振。在文献[10]中,颜等人,针对一类离散不确定时滞系统,提出了一种输出反馈变结构控制算法,基于LMI技术给出了切换面的设计方法。然而以往的研究结果对于切换面的选取并没有统一有效的办法,并且切换面的设计技巧性较强,对于初学变结构控制的学者来说不利于把握。正因为此,本文将给出不同系统的多种设计切换面的策略,在归纳总结前人研究的基础上,针对相变量系统、多输入多输出系统,给出切换面设计的最优控制法,特征向量任置法等,为设计变结构控制打好基础,为初学变结构控制的学者提供帮助。
2主要结果
(1)S>0
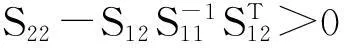
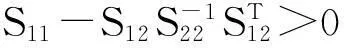
2.1 相变量系统的切换面设计
考虑下面n阶相变量系统
(1)
其中ai(i=1,2,…,n),b均为常数。
选取切换面:
S=c1x1+c2x2+…+cn-1xn-1+xn
其中ci(i=1,2,…,n-1)满足Hurwitz条件。
2.2 利用等效控制设计切换面
考虑下面正则型线性系统
(2)

假设1:系统(2)可控,即(A,B)可控。
选取切换面:
S(t)=Cx(t)
(3)
其中C∈R(n-m)×n为待定的常数矩阵。
把(2)代入(3)式,并求导得到

ueq(t)=-(CB)-1CAx(t)
把上式代入(2)中得到滑模方程
=[I-B(CB)-1C]Ax(t)
由上式知道可以设计系统的状态反馈控制器,因此假设控制器为
u(t)=Kx(t)
(4)
其中K∈Em×n为待定的常数矩阵。
把(4)代入系统(2)得到


从而可以选取切换面系数矩阵C和矩阵W满足

(5)
即可。
定理1对于满足(5)的矩阵C和W,有CW=W
证明:在式子
两边同时左乘以矩阵C得到
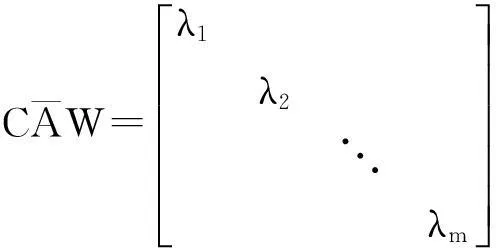
从而CW=0。
2.3 利用二次型最优控制设计切换面
(6)
其中x(t)∈Rn为系统状态,u(t)∈Rm为系统控制输入,矩阵A∈Rn×n,B∈Rn×m为列满秩常数矩阵。
选取系统二次型性能指标为:
J=∫0∞xT(t)Qx(t)dt
(7)
其中Q为半正定对称矩阵。
对系统(6)作变换:
得到


则滑动模态方程为
S(t)=0
其中切换面选为
(8)
其中C1是具有适当维数的矩阵。
由引理1得到



令
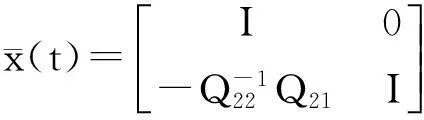
从而性能指标(7)变为
J=∫0∞xT(t)Qx(t)dt

对滑模方程
=A11x1(t)+A12x2(t)
由最优控制得到
2.4 利用极点配置方法选取切换面

选取切换面
(9)
其中C1,C2为具有适当维数的常数矩阵。
滑模方程为
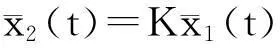
其中C1可取任意非奇异矩阵,如单位矩阵。
令K=-C2-1C1可以确定C2,则滑动方程为:
S(t)=0
取新变量
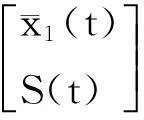
则滑动方程为
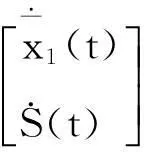
从而
2.5 利用最优控制法设计切换面
对系统(6),选取性能指标为
J=∫0∞xT(t)Qx(t)dt
(10)
其中Q∈Rn×n为正定矩阵。
则
xT(t)Qx(t)
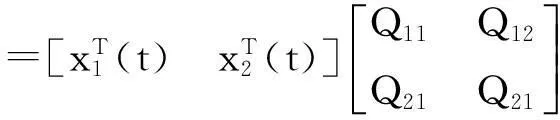
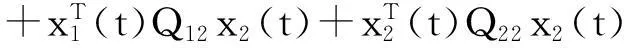
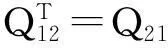
作变换
于是有
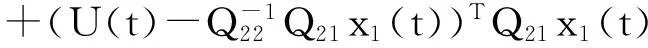
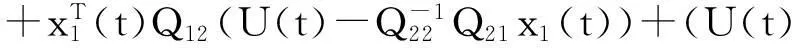

因此滑模方程
就变成了
这样得到一个等价的性能指标
其解为
U(t)=Kx1(t)
其中P是满足
的解。
2.6 利用特征向量任置法设计切换面
对系统(6)选取切换面为
S(t)=Cx(t)
其中C为具有适当维数的常数矩阵。
ueq(t)=-(CB)-1CAx(t)
代入系统(6)中得到
其中
K=(CB)-1CA
令S=Cx(t)=0得到滑动模态在C的零空间,即
ker(C)=N(C)
亦即
C(A-BK)x(t)=0⟺R(A-BK)⊆N(C)
记(A-BK)的特征根为λi(i=1,2,…,n),记λi的特征向量为νi(i=1,2,…,n),则有
C(A-BK)νi=0
亦即
Cλiνi=λiCνi=0
由此可知λi=0或νi∈ker(C)。
已知滑模是n-m维的,等价控制方程要成为滑模必有m个零根。假设n-m个特征根λ1,λ2,…,λn-m的特征向量ν1,ν2,…,νn-m张成ker(C),即
Span(v1,v2,…,vn-m)=ker(C)
于是有
CV=0
(11)
其中V=[v1V2…Vn-m]
由式(11)可解出矩阵C,但其解不唯一。
若将CV=0写成

其中C1,C2为适当维数的矩阵,即
C1V1+C2V2=0
从而得到
C1=-C2V2V1-1
于是切换面的系数矩阵为C
3结论
本文是在前人研究的基础上,针对相变量系统和多输入多输出动力系统,结合Hurwitz稳定性判据和等效控制、极点配置、最优控制、特征向量任置法,得到了多输入多输出动力系统的多种切换面设计方法,系统的归纳总结了切换面设计各种技巧,为变结构控制器的设计与实施做好铺垫,为初学变结构控制的学者提供帮助。
[参考文献]
[1]K.K. Shyu, W.J. Liu, K.C. Hsu. Design of large-scale time-delayed systems with dead-zone input via variable structure control[J]. Automatica, 2005, 41:1239-1246.
[2]X.K. Chen. Adaptive sliding mode control for discrete-time multip-input multip-output systems[J]. Automatica, 2006, 42:427-435.
[3]C.C. Hua, X.P. Guan, G. Duan. Variable structure adaptive fuzzy control for a class of nonlinear time-delay systems[J].Fuzzy Sets and Systems, 2004,148:453-468.
[4]S.W. Kau, Y.S. Liu, A new LMI condition for robust stability of discrete-time uncertain systems[J]. Syst. Contr. Lett.,2005.54:1195-1203.
[5]S.J. Bai, P.B, Q. Zhou, X. Huang. Variable structure controller design for linear systems with bounded inputs[J].International Journal of Control, Automation, and Systems, 2011, (2):228-236.
[6]Y. Niu, B. Chen, Sliding mode control for a class of nonlinear Ito stochastic systems with state and input delays[J]. International Journal of Control, Automation, and Systems, 2009,(7)33:365-370.
[7]Y. Xia, H. Yang, M. Fu, P. Shi, Sliding mode control for linear systems with time-varying input and state delays[J]. Circuits Syst Signal Process, 2011,30:629-641.
[8]L. Liu, Z. Han, W. Li, Global sliding mode control and application in chaotic systems, Nonlinear Dyn, 2009,56:193-198.
[9]于驰,宫明龙,多输入多输出系统的滑模控制器设计及其应用[J].东北大学学报(自然科学版),2012,33(4):473-475.
[10]颜闽秀,井元伟,何友国.一类离散不确定时滞系统的输出反馈变结构控制[J].控制与决策,2009,24(4):499-507.
[责任编辑:Z]
Design of sliding mode surface for dynamical systems in variable structure control classroom teaching
YAO He-jun
(School of Mathematics and Statistics, Anyang Normal University,Anyang 455000,China)
Abstract:Six approaches have been given to design the sliding mode surface for dynamical systems in this paper. Based on the Hurwitz stability criterion、equivalent control、pole-placement method、optimum control、eigenvector method,several approaches have been obtained to design the stable sliding mode surface and the variable structure controller.
Key words:Sliding mode control; Discrete-time systems; Large-scale system with delays
[中图分类号]TP273
[文献标识码]A
[文章编号]1671-5330(2015)02-0121-05
[作者简介]姚合军,男,副教授,主要从事动力系统方面的教学与研究。
[收稿日期]2015-01-29
