分布式电源在配电网中布点规划研究

李 宁

(吉林敦化抽水蓄能有限公司，吉林敦化133700)

分布式发电(Distributed Generation，简称DG)是指为了满足一些特殊用户的需求，支持已有的配电网的经济运行而设计和安装在用户处或其附近的小型发电机组(一般小于30MW)以及安装在用户附近用于提高负荷的供电可靠性和电能质量，或者由于就地应用热电联产使效率得到提高的发电形式。由于大电网中任何一点的故障都可能对整个电网带来严重的影响以及在一些比较偏远地区，距离电力系统太远，或者自然条件太恶劣，输配电建设投资过大或者根本就无法架设，导致供电不理想，且全球的一次能源正日渐衰竭，而由电力生产所带来的环境污染也越来越明显。然而分布式发电的使用不仅能优化电网结构，降低网络损耗，实现经济运行，而且能提高电力系统运行的稳定性和可靠性，具有污染少，能量利用率高的优点。因此，大电网与DG相结合的方式是未来的发展方向。

然而随着分布式发电技术的逐步推广，分布式电源的位置和容量的选择对配电网的节点电压、线路潮流、短路电流、网络可靠性等都会带来影响。因此，对分布式电源进行合理选址定容十分重要［1－5］。

国内外己有一些学者对分布式电源选址和定容问题进行了研究。文献［6］在考虑新增负荷节点的情况下，由新增负荷总量确定待建分布式电源的总容量，采用遗传算法及基于支路交换的模拟退火算法进行网络扩展规划，得到分布式电源和配电网络的综合优化方案。文献［7］在给定分布式电源容量情况下，采用解析法研究了单条辐射线路上分布式电源的最优安装位置。文献［8］提出了一种空间决策支持系统用于确定分布式电源的允许安装位置。文献［9］在分布式电源个数、位置和容量都未知的情况下，采用遗传算法对分布式电源的位置和容量进行优化。文献［10］提出了基于遗传算法和决策理论的三步式方法用于中压网络中分布式电源的最优位置和规模的确定。

本文在分布式电源个数、位置和容量都未知的情况下，以折算到每年的分布式电源的投资及运行费用和线路建设运行费用最小及引入分布式电源后购电费用最小为目标函数，建立含分布式发电的经济性模型，首先采用前推回代法对含分布式电源的配电网进行潮流计算，再用遗传算法优化分布式电源的位置和容量，最终得到分布式电源的优化配置方案。

1 含分布式电源的线路负载能力及潮流计算

1.1 含分布式电源的线路负载能力

由于分布式电源一般安装在负荷中心附近，这里假设分布式电源安装在负荷节点上。

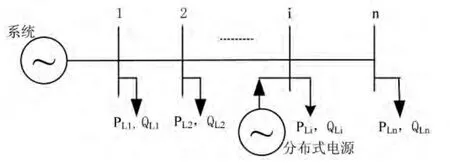
图1 带分布式电源的辐射线路

图1所示为一条辐射型线路，假设分布式电源安装在该条路径的第i个负荷节点上，根据节点上的负荷与分布式电源的有功大小关系得到负荷在配电网中的有功流动情况:

(1)PDG＞Pli时，该负荷节点可看成是一个向配电网供出PDG－Pli有功的电源节点;

(2)PDG=Pli时，配电网和该负荷节点间没有有功流动;

(3)PDG＜Pli时，配电网向该负荷节点提供Pli－PDG有功;

经过分析得出分布式电源的加入可能使线路潮流的流向发生改变，而配电网中系统保护是根据线路潮流单向流动这一特性进行设计，因此，为使电网中接入分布式电源后潮流流向不发生改变，配电网中所安装的分布式电源容量不超过所在节点的负荷大小，即PDG≤Pli。

1.2 含分布式电源的线路潮流计算

因分布式电源所采用的模型［11］可简化为PV或PQ节点，本文将其视为具有恒定功率因数的PQ节点。采用前推回代法［12］进行含分布式电源的配电网潮流计算，方程描述如下:

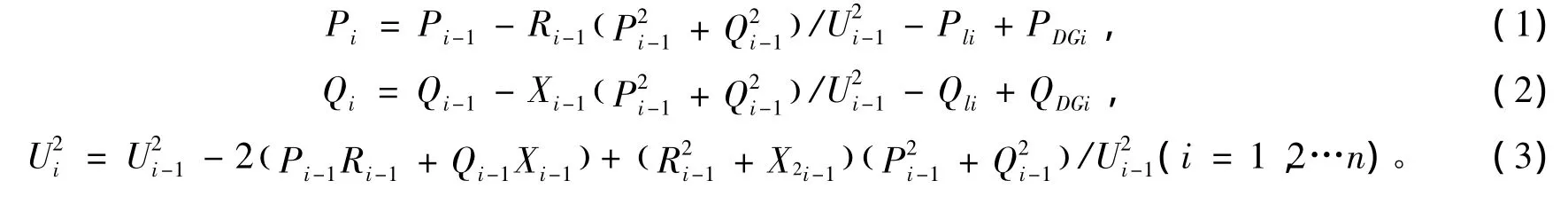
2 分布式电源选址定容的优化模型

分布式电源的布点规划即在不改变现有配电网结构的前提下考虑负荷的增长，通过合理的接入分布式电源来满足负荷的需求。本文假定配电网规划期限为20年，负荷需求以每年1%的速度增长(模型中不考虑变电站扩建费用)。建立含分布式电源配电网规划的经济性模型描述如下:

2.1 目标函数

CDG=为折算到每年的分布式电源的投资及运行费用;

其中:nDG为接入配电网的分布式电源个数;αi为第i个分布式电源的固定投资年平均费用系数;CDGi为第i个分布式电源的固定投资费用(万元);Cpu为单位电价(元/kWh);ΔEDGi为第i个分布式电源的年电量损失总值(万kWh);WDGi为第i个分布式电源的检修、维护费用(万元为折算到每年的线路运行费用;Cpu为单位电价(元 /kWh);τmax为第i条支路的年最大负荷损耗小时数(h);ΔPli为第i条支路上的有功损耗(万kW)为购电费用;Τmax为最大负荷年利用小时数;P∑新增为新增负荷总量;P∑DG为分布式电源的总有功出力为分布式电源i的功率因数;SDGi为第i个分布式电源的容量。

2.2 不等式约束条件

(1)节点电压约束

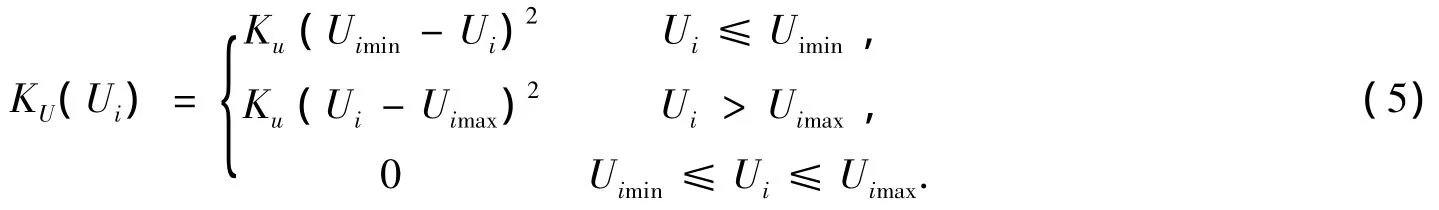
式中:Ui为节点i的电压;Uimin、Uimax分别为Ui的上下限;KU为节点电压惩罚因子，作为对偏离运行极限的惩罚，一般取值较大，满足要求时则取值为O。

(2)导线电流不等式约束［22］

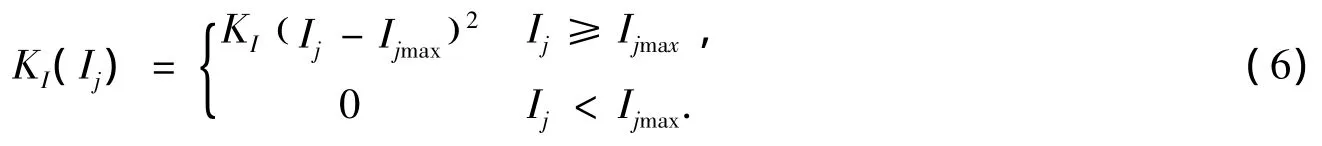
式中:Ij为支路j的电流;Ijmax为第j条支路允许通过的电流上限;KI为导线电流惩罚因子，取值的原则同KU。

(3)分布式电源运行约束

式中:假设在电网中分布式电源的最大接入容量不超过最大负荷总量的10%［13］，S∑DG为分布式电源接入电网的总容量;SL为电网总负荷的10%;K∑DG为分布式电源注入量惩罚因子，取值原则同KI。将上述模型的不等式约束以惩罚因子的形式并入归一化目标函数，所得新的目标函数为:

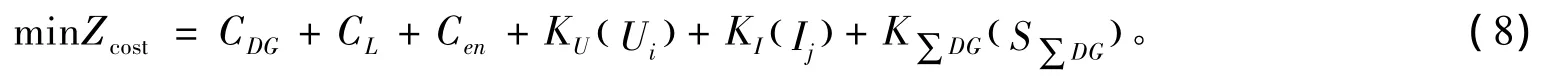
3 分布式电源布点规划的求解步骤

3.1 染色体编码

本文对分布式电源的位置和容量变量采用实数编码［14］的方法，同时假设各分布式电源安装在负荷节点上，且一个负荷节点安装一个分布式电源。。

3.2 产生初始群体

在优化过程中，采用随机方式产生初始解，具体产生步骤如下:

(1)由待规划电网新增负荷总容量确定分布式电源总容量;

(2)随机产生一个初始群体，并对该群体所有个体进行校验。

3.3 遗传算法的实现

遗传算法从初始群体出发，以适应度函数为依据，通过对群体进行选择、交叉、变异的操作使群体达到最优，所采用的3种遗传算子如下:

(1)选择(复制)算子

本文对于选择(复制)算子采用最优保存策略，保证了当前群体中的最优个体的适应度不低于前代群体的适应度。

(2)交叉算子

采用改进的“自适应交叉算子”，调整公式如下:

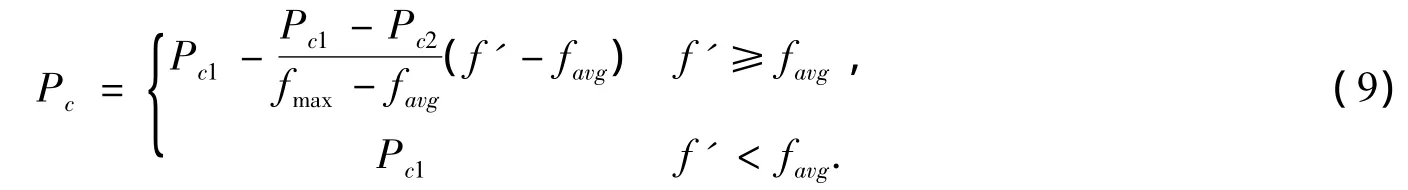
式中:fmax代表群体中最大的适应度值;favg代表每代群体的平均适应度值;f'代表要交叉的两个个体中较大的适应度值。

交叉概率选择 Pc1=0.9，Pc2=0.4［15］。

(3)变异算子

采用改进的“自适应变异算子”，调整公式如下:

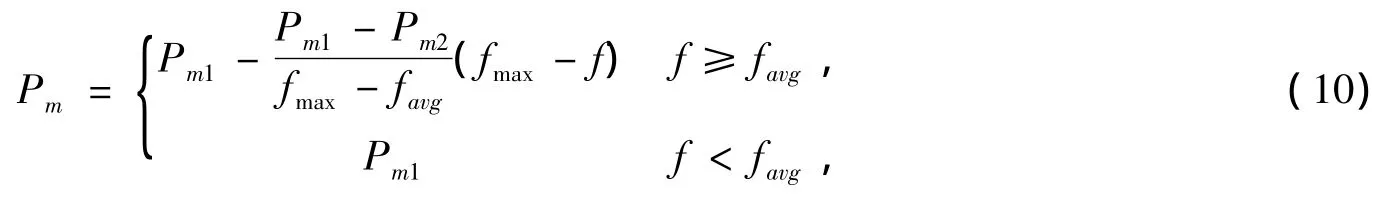
式中:fmax代表群体中最大的适应度值;favg代表每代群体的平均适应度值;f代表要变异个体的适应度值。

变异概率选择 Pm1=0.1，Pm2=0.001［9］。

3.4 搜索终止条件

一般来说，遗传算法优化搜索的终止条件有以下三个，其中满足任何一个条件搜索就结束，本文采用达到遗传操作的最大迭代次数Ncmax。

4 算例分析

本文把分布式电源视为具有恒定功率因数的PQ节点。这里假设待选的单个分布式电源的功率因数η =0.9，容量为0.1 MVA的整数倍，且不大于所安装节点的负荷量PDG≤Pli［16］，最大接入容量为最大负荷总量的10%。关于交叉概率、变异概率的选取如下:群体大小为M=60，交叉概率Pc1=0.9，Pc2=0.4，变异概率Pm1=0.1，Pm2=0.001，最优保存个数取2，最优解连续不变最大代数W=5，最大迭代次数Nc=100，收敛判据ε=0.000 1。年最大负荷利用小时数τmax=3 000 h，单位电价Cpu=0.5元 /kW·h，惩罚系数KU=KI=K∑DG=100，分布式电源的固定投资年平均费用系数αi=0.35。

算例采用IEEE33节点系统，其结构如图1所示。网络中允许接入分布式电源节点为节点2～节点33。

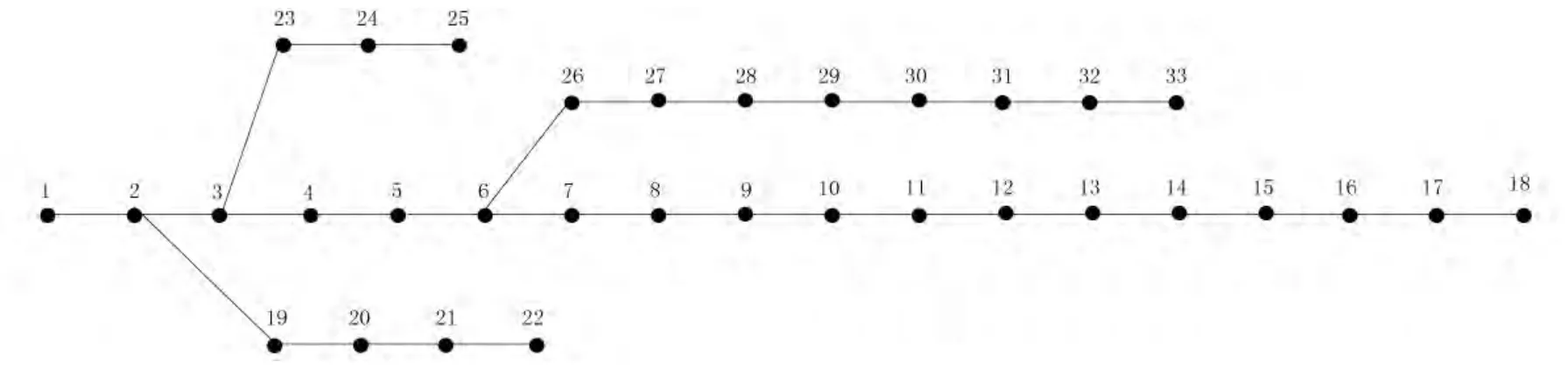
图2 算例的初始网架

应用算法，经过仿真分析，我们可以得出:

(1)改进自适应遗传算法和标准遗传算法收敛性对比图:

图3 图表

由图3可知，改进的自适应遗传算法保证了遗传算法的收敛能力，避免了“早熟”现象，有效地提高了遗传算法的优化能力。

(2)分布式电源布点规划优化结果

由仿真结果得知，分布式电源安装于负荷节点3、15、16、31，安装容量如表1所示。

由表1得出，分布式电源主要分布在辐射状配电网的末端。系统接入DG后的有功网损为86.6kW，系统未接入DG时的有功网损为190kW，优化后的有功网损下降了54.442%，由此可得出对分布式电源进行优化配置能够有效的降低网络损耗。

表2为含分布式电源和不含分布式电源两种情况下的电网运行费用比较。

从网损方面看，接入分布式电源后，对配电网进行合理地规划，可以有效的降低线路年费用。

表1 分布式电源的接入位置和容量

表2 不同规划方案的费用比较

5 结 论

通过遗传算法对配电网中分布式电源的位置和容量进行优化配置，在IEEE33节点网络中验证了此方法的有效性。尽管目前分布式电源的发电成本比较高，但是对分布式电源进行布点规划可明显降低购电费用，并有效降低网损。因此在配电网中引入分布式发电，在满足一系列约束条件下，能得出较优的规划方案，找到较优的规划点，其具有良好的经济效益和社会效益。

［1］王建，李兴源，邱晓燕.含分布式发电装置的电力系统研究综述［J］.电力系统自动化，2005，29(24):90－97.

［2］梁才浩，段献忠.分布式发电及其对电力系统的影响［J］.电力系统自动化，2001(6):53－56.

［3］BOIRGCES C LT FALCAO DM.Impact of Distributed Generation allocation and sizing on reliability losses and voltage profile［J］.Proceedings of IEEE Power Tech Conference Bologna(Italy);2003.

［4］崔金兰，刘天琪.分布式发电技术及其并网问题研究综述［J］.现代电力，2007，3(24):53－57.

［5］王志群，朱守真，周双喜.分布式电源对配电网电压分布的影响［J］.电力系统自动化，2004，28(16):56－60.

［6］王成山，成凯，谢莹华，郑海峰.配电网扩展规划中分布式电源的选址和定容［J］.电力系统自动化，2006，30(3):38－43.

［7］Mutale J.Strbac G，Curcic et al.Allocation of Losses in Distribution Systerm with Embedded［C］.IEEE Proceeding of Generation Transmission and Distribution.UK，April，2000，32:146－164.

［8］New York State Energy Research and Development Authority.Combined Heat and Power market potential for New York State final report.Octorber 2002，438－440.

［9］DU grand R C，McDermott T E.Operating Conflicts for Distribution Generation on Distribution System Distribution System.Rural Electric Power Conference，2001.

［10］孙建国，冯志兵.冷热电联产系统的发展及前景［J］.燃气轮机技［J］.2006，31(9):113－118.

［11］段玉倩，贺家李.遗传算法及其改进［J］.电力系统及其自动化学报，1998，10(1):39－52.

［12］颜伟，刘方，王官洁.辐射型网络潮流的分层前推回代算法［J］.中国电机工程学报.2003，23(8):76－80.

［13］周明，孙树栋.遗传算法原理和应用［M］.北京:国防工业出版社，1999.

［14］邹琳，夏旦堪，胡国安.基于实数编码的多种群并行遗传算法研究［J］.小型微型计算机系统.2004，25(6):982－986.

［15］许明辉，搞成修，于刚.一种克服遗传算法早熟的参数调整及并行方法［J］.武汉理工大学学报:理学版，2001，47(1):33－35.

［16］王志群，朱守真，周双喜等.分布式发电接入位置和注入容量限制的研究［J］.电力系统及其自动化学报.2005，(1):53－58.

［17］张奇.配电网规划中分布式电源的选址和定容［D］.济南:山东大学，2008.

［18］段玉倩，贺家李.遗传算法及其改进［J］.电力系统及其自动化学报，1998，10(1):39－52.

［19］马少平，朱小燕.人工智能［M］.北京:清华大学出版社，2004.

［20］蔡丽霞.含分布式电源的配电网规划研究［D］.北京:华北电力大学，2007.