粘附性颗粒流化特性研究及信息熵分析

郑建祥，朱秀丽

(1.东北电力大学能源与动力工程学院，吉林吉林132012;2.东北电力大学理学院，吉林吉林132012)

粘附性颗粒可归为C类粒子，其表面有有很强的粘性力，在气流作用下会发生聚团，可实现聚团流化。它广泛应用与工厂，矿山，石油化工及药品制备方面，在这些应用中，对颗粒的输运需要对其进行流化，所以现在颗粒聚团物的流态化行为的研究逐渐成为研究的热点。Venkatesh等［1］在锥形圆柱体内对C类颗粒流化特性进行了实验研究。Wank等［2］对氮化硼细颗粒在低压下的震动流化进行了实验研究。Jung＆Gidaspow［3］对纳米级尺寸颗粒流化和塌落行为进行了实验研究。郑建祥等［4］对弹性恢复系数对超细颗粒碰撞影响进行模拟研究。尽管国内外对粘附性颗粒聚团流态化过程进行了实验研究，但理论数值模拟工作开展的较少。传统的双流体模型如何进行完善，以适应小尺寸粘附性颗粒流动特性的数值研究是急待解决的问题。本文基于双流体模型，考虑气相和纳米颗粒聚团间及聚团之间的动量和能量的传递和耗散，建立纳米颗粒聚团固相粘度系数、纳米颗粒聚团压力等物性参数计算模型;并采用周涛颗粒团能量平衡计算模型预测颗粒聚团当量直径［5］，数值模拟得到流化床内粘附性颗粒流动特性。

1 数学模型

为简化研究，假设提升管内气体和颗粒是等温流动，气相和颗粒相间无质量交换。基于质量、动量和能量守恒定律可建立提升管内气相和颗粒相流动模型。

1.1 连续性方程(k=g时为气相，k=s时为颗粒相)

式中，ρk为k相密度，εk表示k相体积浓度，vk为k相速度，t为时间。

1.2 气相动量守恒方程

式中，Pg为气相压力，g为重力加速度，β为气固相间曳力系数，τg为气相应力张量:

其中，μg，l为气体层流动力粘度，μt为气体湍流动力粘度。假定气体不可压缩，密度为常量。气相湍流采用大涡模拟方法，气相动力粘性系数:

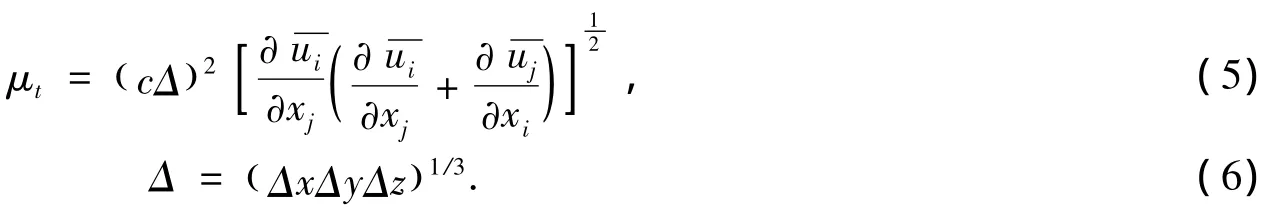
1.3 固相动量方程

式中，τs为固相应力张量:

其中，固相压力Ps、颗粒相剪切粘度μs和颗粒相动力粘度ξs为:

式中，粘性压力系数 ξp1(Rc)为

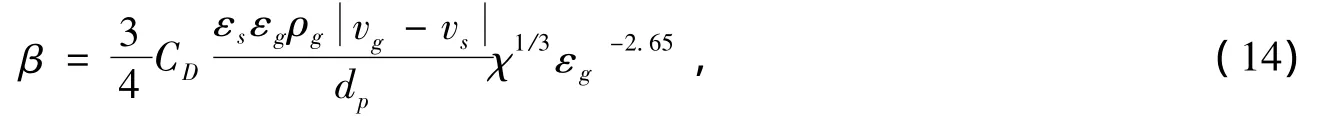
式中，

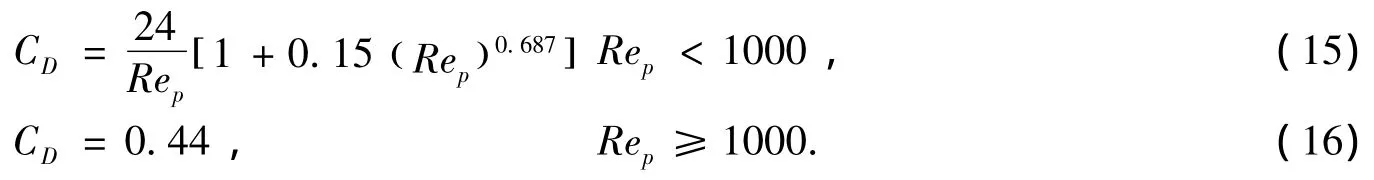
1.4 颗粒脉动能量方程

颗粒脉动主要是由于颗粒间相互碰撞和颗粒与气体湍流相互作用的共同作用引起的。类似于气体温度衡量气体分子的运动一样，定义颗粒温度为:q=u'2/3，其中，u'为颗粒脉动速度。颗粒脉动动能守恒方程可表示如下:

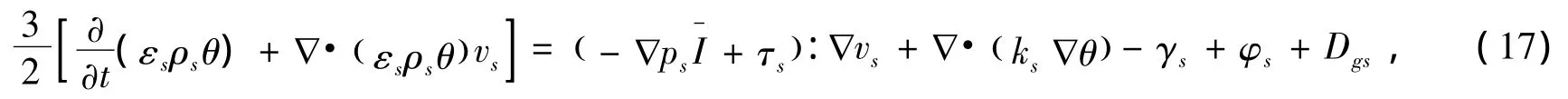
式中，颗粒间碰撞能量耗散率γs和脉动能量传递系数k分别为［6］:

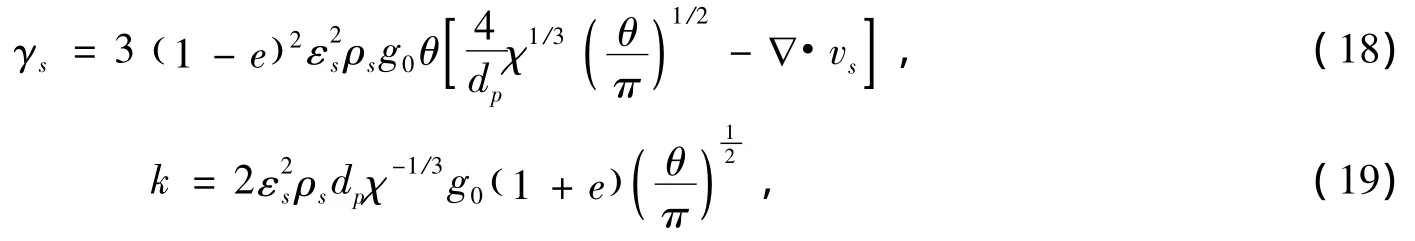
g0是颗粒径向分布函数。颗粒径向分布函数可按Bagnold方程［7］确定:

其中，εs，max是填充状态下最大颗粒浓度。

Dgs是单位体积能量耗散率。基于分子动力学，Koch’s建立颗粒能量耗散率计算模型［8］:

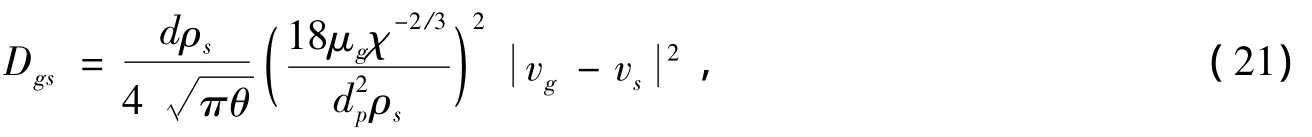
气相与颗粒相脉动能量的交换为:

1.5 颗粒团聚物当量直径

聚团尺寸估算模型采用力平衡模型［5－9］，假定聚团为球形，不考虑壁面的影响;忽略静电力和液桥力的作用。计算公式表示为:

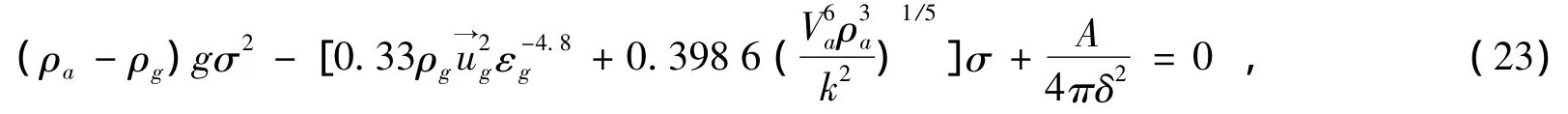
式中:A表示Hamaker常数，δ表示聚团间距离。流化床模拟结构如图1所示，计算数据来源于Li等［9］的实验数据。内径75 mm，高3 250 mm。采用TiO2颗粒作为流化颗粒。颗粒初始直径为0.2 mm，颗粒密度为3 880 kg/m3，聚团密度为886 kg/m3。颗粒间及颗粒与壁面间弹性碰撞恢复系数分别取为0.99和0.9。计算总时间为20 s，最后15 s作为时间平均值的计算样本。

2 模拟结果及讨论

图2给出不同时刻下的瞬时颗粒浓度分布。从图中可以看出，纳米颗粒聚团流动呈典型的“S”型环核流动结构，中心颗粒聚团向上流动，壁面颗粒聚团向下回落。在提升管下部颗粒聚团浓度较高，主要集中在两壁区域。在提升管上部，颗粒聚团浓度分布则较为均匀，而在顶部出口区域，由于出口的转向因素，形成较高聚团浓度区。

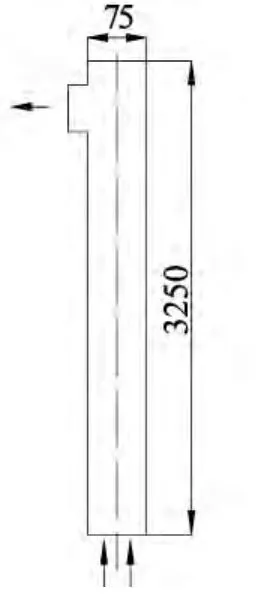
图1 流化床结构示意图

图2 不同时刻瞬时浓度

图3表示在进口气体速度为1.89 m/s和2.20 m/s、质量流量为3.15 kg/m2s时，颗粒聚团截面平均浓度的轴向分布。从图上可以看出，颗粒聚团浓度是下浓上稀。随着入口进气速度的增加，浓度沿轴向分布整体减少，浓度分布趋于均匀。模拟结果与Li等的实验结果吻合的很好。

图4表示在不同进口气体速度下质量流量为3.15 kg/m2s时颗粒聚团截面平均直径的轴向分布。由图可知，在床层底部，均出现了大颗粒聚团。在床层中上部，聚团尺寸分布落差较小，分布较为均匀。随着入口进气速度增加，底部颗粒聚团尺寸变小。故从中可知，改变入口速度将直接影响聚团尺寸大小。

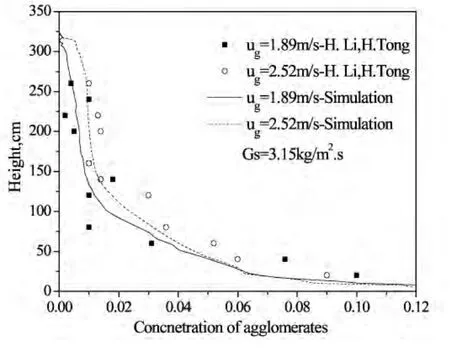
图3 聚团浓度的轴向分布

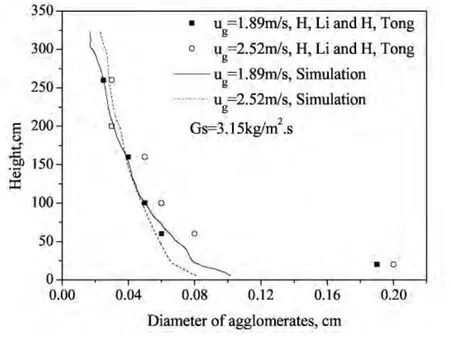
图4 聚团直径的轴向分布

3 模拟结果Shannon信息熵分析

气固流化床中压力、温度和浓度等脉动信号体现了气固运动的大量信息，是床内气固两相流体动力学众多内在因素的综合反映。分析这些信号可以得到两相流动特征。其分析方法有小波分析［10］和混沌［11］等方法。引入信息熵分析两相流信号则刚刚兴起。Cho等［12］采用信息熵研究了三相循环流化床中温度的脉动，李洪伟等［13］讨论了汽液两相场的混沌特征。黄轶伦等［14］对气固流化床中的信息熵进行了研究，提出信息熵通过床内粒子的扰动三维传输的观点。Zhong等［15］对喷动床内流型和信息熵之间的关系进行分析。

流化床内时间序列浓度信号{x1，x2，…，xn}的Shannon信息熵的定义如下:

式中:n为时间序列信号的长度;p(xi)为每个随机信号发生的概率，满足，采用联合概率密度公式进行计算。

图5表示利用速度为1.89m/s，质量流量为3.1 5 kg/m3s工况得到时间序列浓度信号计算出来的不同高度的Shannon信息熵分布图。由前面的分析可知，粘附性颗粒聚团气固两相流动形式是“S”型环核流动，中间区域颗粒聚团在摆动情况下，聚团碰撞脉动较壁面附近剧烈，所以其信息熵值较大。随着高度增加，气流的携带作用减弱，在重力作用下，聚团回落引起的碰撞加强，所以其Shannon信息熵值逐渐增大，说明在流化床上方，聚团流动不是很稳定。但由Shannon信息熵计算值判断，其计算值在1～10 db之间，此工况还是很稳定的。在出口H=3.12 m处，由于出口转向引起的颗粒聚团聚集形成局部高浓度区，此处信息熵值较高。

4 结 论

应用双流体模型对粘附性颗粒聚团的流化过程进行了数值模拟研究。模型中考虑气相和颗粒聚团间及颗粒聚团之间的动量和能量的传递和耗散，建立粘附性颗粒聚团固相粘度系数、聚团压力等物性参数计算模型;并采用周涛颗粒团能量平衡计算模型预测颗粒聚团当量直径，对流化床内粘附性颗粒聚团流动特性进行数值模拟。

模拟结果表明:

(1)颗粒聚团在流化床内流动是典型的S型环核流动。

(2)大颗粒聚团主要分布在提升管底部和边壁环型高浓度区，小颗粒聚团则分布在低浓度区。

(3)利用Shannon信息熵分析粘附性颗粒聚团流化的混沌特性，分析结果为聚团流化中床内浓度的信息熵在1－10之间。在床层升高，信息熵值变大。说明在床层上部聚团与气体间，聚团与聚团间的脉动变化比较剧烈。

［1］Venkatesh R.D.，J.Chaouki，D.Klvana.Fluidization of cryogels in a conical column［J］.Power Technology，1996，89:179－186.

［2］Jeffrey R.W.，S.M.George，A.W.Weimer.Vibro－fluidization of fine boron nitride powder at low pressure［J］.Powder Technology，2001，121(6):195－204.

［3］Jung J.，D.Gidaspow.Fluidization of nano－size particles［J］.Journal of Nanoparticle Research，2002，6(4):483－497.

［4］郑建祥，刘洪雷，弹性恢复系数对超细颗粒气固流场影响的研究［J］，东北电力大学学报，2010，30(6):10－14.

［5］周涛.粘性颗粒聚团流态化实验与理论研究［D］.北京:中国科学院化工冶金研究所，1998:55－60.

［6］郑建祥，吕太，脱硫塔内气固流场数值模拟－稠密颗粒动理学方法［J］，东北电力大学学报，2012，32(2):38－42.

［7］R.A.Bagnold.Experiments on a gravity－free dispersion of large solid spheres in a Newtonian fluid under shear［M］.Proc.R.Soc..London，1954，A225:49－63.

［8］D.L.Koch，A.S.Sangani.Particle pressure and Marginal stability limits for a homogenous monodisperse gas－fluidized bed:Kinetic theory and numerical simulations［J］.J.Fluid Mech.1999，400(6):229－263.

［9］H.Z.Li，H.Tong.Multi－scale Fluidization of Ultrafine Powders in a Fast－bed－riser/conical－dipleg CFB Loop［J］.Chemical Engineering Science.2004，59(8－9):1897－1904.

［10］黄海，黄轶伦.气固流化床压力脉动信号的Hilbert－Huang谱分析［J］.化工学报.2004，55(9):1141－1147.

［11］王轶，王亭杰.金涌.振动流化床中流动结构的混沌分析［J］.化工学报.2003，54(12):1696－1701.

［12］Y.J.Cho，S.J.Kim，S.H.Nam，Y.Kang，S.D.Kim.Heat Transfer and Bubble Properties in Three－phase Circulating Fluidized Beds［J］.Chemical Engineering Science.2001，56(21/22):6107－6115.

［13］李洪伟，周云龙，刘旭.基于主成分分析与支持向量机回归的气液两相流容积含气率的测量［J］.东北电力大学学报.2012，32(1):35－40.

［14］黄轶伦，黄海，陈伯川.复杂性在气固流化床流型识别中的应用［J］.高校化学工程学报.2004，18(4):453－458.

［15］W.Q.Zhong，M.Zhang.Characterization of Dynamic Behavior of a Spout－fluid Bed with Shannon Entropy Analysis［J］.Powder Technology，2005，159(2):121－126.