基于最小二乘原理的组合模型在建设用地需求量预测中的应用

2015-02-19彭明军潘琛玲肖立霞

测绘通报 2015年3期

关键词：建设用地预测

孟　成，彭明军，潘琛玲，夏　希，肖立霞

(武汉市国土资源和规划信息中心，湖北武汉 430014)

Forecasting of Construction Land Demand Based on the Composition

Model of the Principle of Least Squares

MENG Cheng，PENG Mingjun，PAN Chenling，XIA Xi，XIAO Lixia

基于最小二乘原理的组合模型在建设用地需求量预测中的应用

孟成，彭明军，潘琛玲，夏希，肖立霞

(武汉市国土资源和规划信息中心，湖北武汉 430014)

Forecasting of Construction Land Demand Based on the Composition

Model of the Principle of Least Squares

MENG Cheng，PENG Mingjun，PAN Chenling，XIA Xi，XIAO Lixia

摘要：通过分析武汉市2002—2011年建设用地数据，选取了三次指数平滑、灰色GM(1,1)模型和多因素回归法建立组合模型，提出了一种基于最小二乘原理解算组合系数的方法，并对武汉市2012—2025年的建设用地需求量进行了预测。经过计算预测结果的平均绝对百分误差、均方根误差及希尔不等系数，证明了该组合模型可信度高，可用于武汉市土地利用规划编制工作。

关键词：建设用地；预测；组合模型；最小二乘原理

一、引言

近年我国城市经济高速发展，土地资源供不应求的情况时有发生，同时还伴随着耕地面积减少、农村土地质量退化、人地矛盾加剧等诸多问题[1]。因此，土地资源的合理规划对均衡城市用地、合理开发城市资源、促进城市健康增长具有重要意义，而建设用地需求量分析是土地利用总体规划的核心。目前，国内外学者在建设用地需求预测方面形成了大量的研究方法和模型，可归纳为定额指标法、时序预测法、因素预测分析法、控制预测法及目标约束法积累。在实际应用中，不同方法往往只能提供某一方面信息，而丢失另外一些有用信息[2]。基于这种事实，有研究者提出采用组合模型对建设用地进行预测的方法，即对同一个问题,采用两种以上不同模型进行预测[3]。本文在基于传统方法解算组合系数的基础上，提出了一种基于最小二乘原理解算组合系数的思想，其组合模型较经传统方差倒数法解算的组合模型预测精度高。

二、组合模型基本原理

1. 组合模型概念

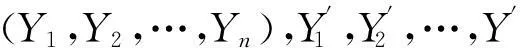
2. 组合系数的确定方法

在组合模型的使用中，通常采用方差倒数法判断单项模型系数，即对误差平方和小的模型赋予较高的权重，误差平方和大的赋予较小的权重，使组合模型的误差平方和尽可能地小。公式如下

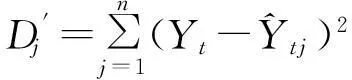
本文通过最小二乘原理解算模型系数，即将真实值作为因变量，单项模型的预测值作为自变量，拟合出一条曲线，使之在坐标系上与已知数据之间的距离的平方和最小，模型的系数即为通过最小二乘原理解算出来的自变量的系数。将Yt作为因变量、Ytf作为自变量，建立回归方程

Yt=K×Ytf+b

根据最小二乘原理解算回归系数为

3. 精度评定

预测领域通常采用平均绝对百分误差(MAPE)、均方根误差(RMSE)和希尔不等系数(Theil IC)判断预测结果的优劣[4]。其中，MAPE低于10则预测精度较高，Theil IC一般介于0~1，且值越小，说明拟合程度越高。公式如下

三、数据分析

可将预测模型分为两大类：一类是用自身前期变化来描述以后情况的自回归模型；另一类是通过研究与之变化相关的其他因素，从而描述以后情况的多因素回归模型。

1. 自回归分析

本文以2002—2011年武汉市建设用地数据作为样本(见表1)，分别选择指数趋势线、线性方程趋势线和二次多项式趋势线对原序列拟合，并计算相关系数R2值。R2值越接近1，表明拟合曲线与原序列相关性越高(如图1(a)所示)。其中，原序列二次多项式曲线的R2=0.994 1，在3种趋势线中拟合效果最好，可选取三次指数平滑法进行预测。选取指数趋势线拟合累加序列，其R2为0.958 5，拟合效果较好，可采用灰色模型GM(1,1)进行预测(如图1(b)所示)。数据的年增长率变化幅度大较，因此不宜采用年均增长率法进行预测(如图1(c)所示)。

表1　2002—2011年武汉市建设用地面积、年增长率、累加面积

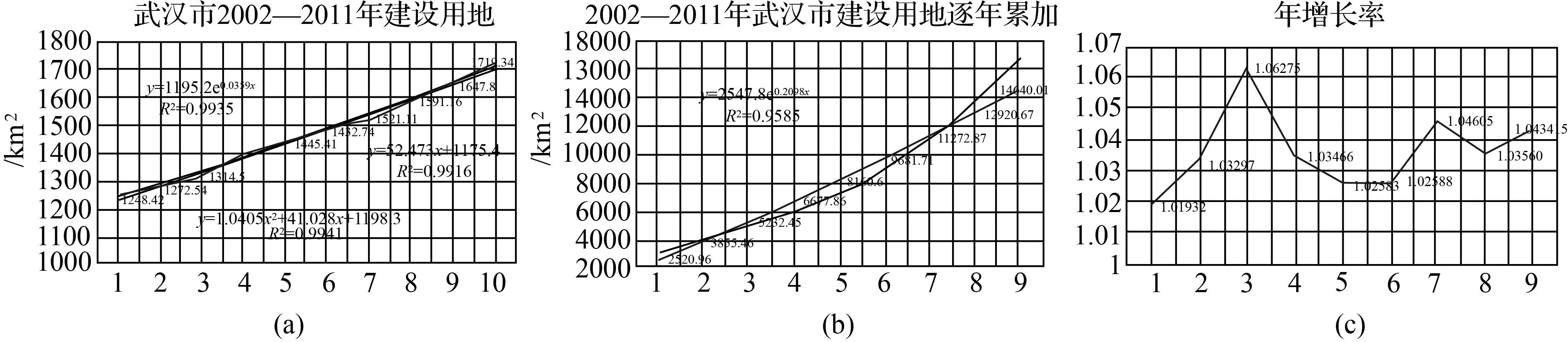
图1　武汉市2002—2011年建设用地、逐年累加值、年增长率折线图

2. 多因素回归分析

本研究为了既不损失预测精度又提高计算效率，在驱动因子的选取时，剔除有线性关系的因子，如选取总人口后，就不再选取城镇人口和农村人口作为驱动因子。根据此原则，在参阅相关文献[5—7]后，最终选取总人口、总GDP、固定资产投资、人均道路面积、路网密度、人均绿地面积作为待分析因子，见表2。

表2　2002—2011年相关驱动因子信息表

续表2

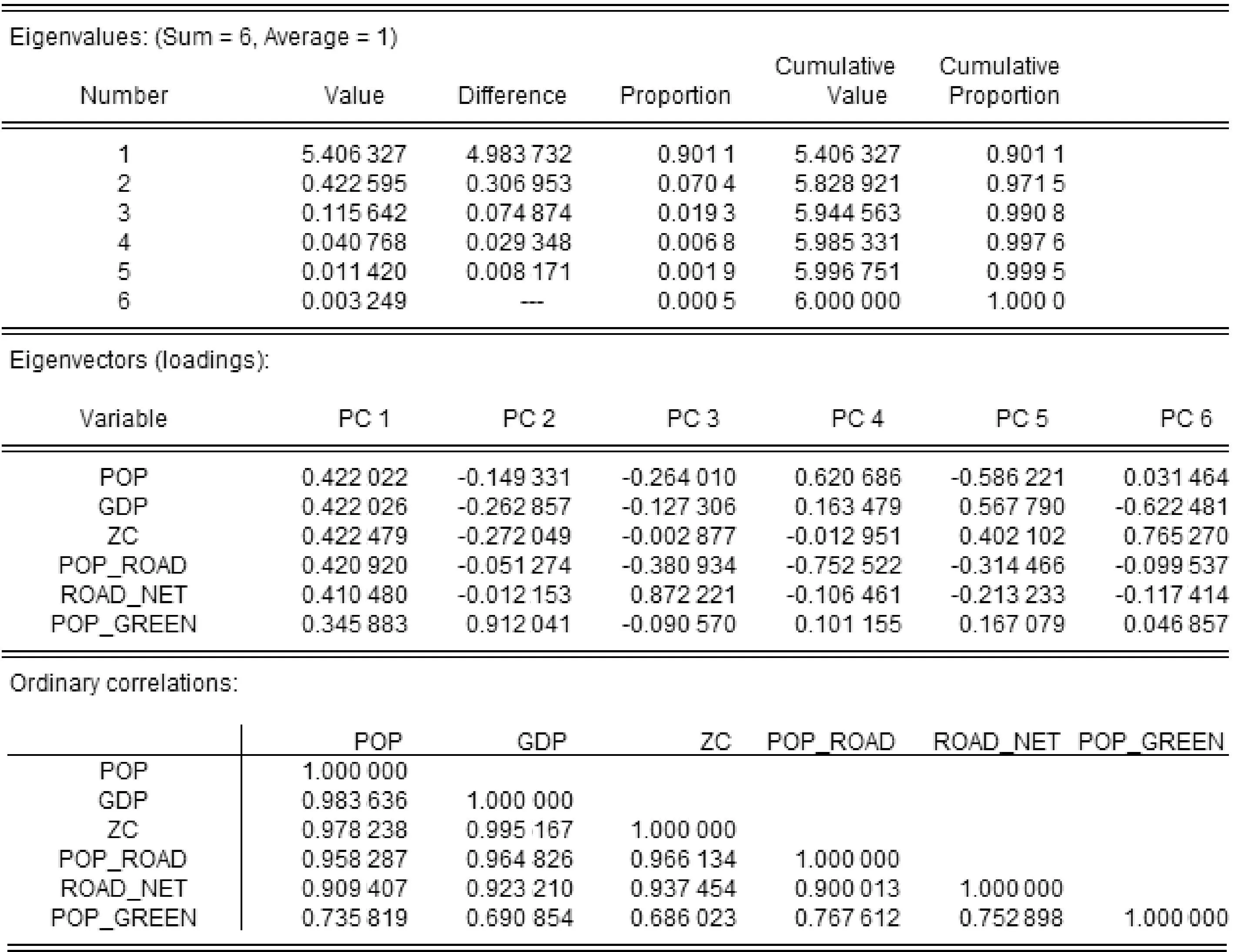
图2　驱动因子主成分分析结果

通过Eviews软件对6个驱动因子进行主成分分析，得到结果如图2所示。其中，POP表示总人口，GDP表示总GDP，ZC表示固定资产投资，POP_ROAD表示人均路面，ROAD_NET表示路网密度，POP_GREEN表示人均绿地面积。第1个成分占总方差的90.11%，第2个成分占7.04%，第3主成分占1.93%，前3个成分占总方差的99.08%。分析可知，前3个指标包含了全部6个指标中99.08%的信息，能够充分代替原来6个指标。主成分公式如下

四、建设用地需求量预测

1. 单项模型预测

通过组合模型进行建设用地需求量预测，首先需分别通过各单项模型进行预测，再将预测结果进行组合求解。本研究中各单模型预测通过Matlab编程实现，结果见表3。

2. 建立组合模型预测

通过各单项模型计算2002—2011年建设用地模拟值并与2002—2011年真值比较，分别计算采用方差倒数法和最小二乘法得到组合模型系数，结果见表4。

分别以2002—2011年武汉市建设用地真实值和各单项模型、两种组合模型的模拟值计算平均绝对百分误差、均方根误差及希尔不等系数来判断预测结果的优劣，结果见表5。

从结果可知，采用最小二乘原理建立的组合模型预测精度优于任一单项模型预测精度和方差倒数法建立的组合模型预测精度。因此，本研究选用最小二乘原理解算组合系数，建立组合模型。通过组合模型预测2012—2025年武汉市建设用地需求量，其预测结果见表6。公式为

Y最小二乘=0.21X指数平滑+0.77XGM+0.02X多因素

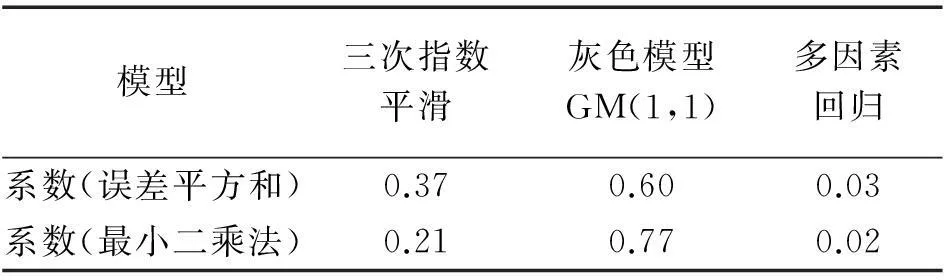
表4　模型误差平方和及组合系数

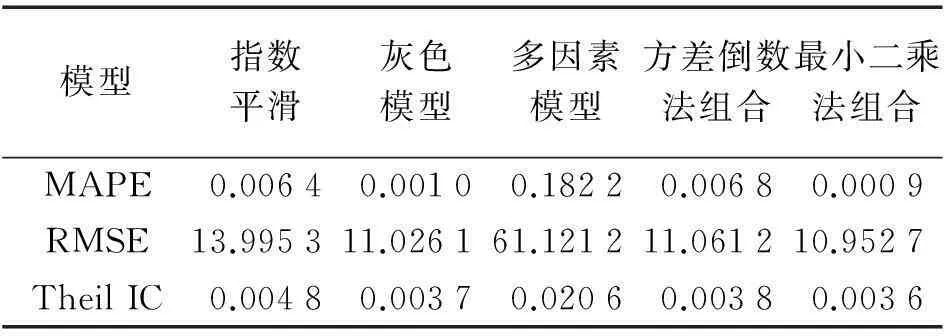
表5　各模型的MAPE值、RMSE值、Theil IC值

表6　组合模型预测武汉市2012—2025年建设用地需求量　km2

五、结束语

在采用组合模型进行预测时，需要选取既有较高预测精度，又能充分反映数据变化趋势的模型，在模型数量的确定上需兼顾预测精度与工作量，在模型系数的确定上需依据组合模型的预测精度高于任一单项模型预测精度的原则，同时根据实际情况尝试多种组合系数解算方案，最终选取预测精度最高的方法解算模型系数建立组合模型。

本文针对武汉市2002—2011年建设用地数据特点及该时期武汉市社会经济情况，通过自回归分析和多因素回归分析，选取三次指数平滑模型、灰色GM(1，1)模型和多因素回归模型进行组合，采用最小二乘原理解算模型系数，最后通过该组合模型预测了武汉市2012—2025年的建设用地需求量，通过分析预测值平均绝对百分误差、均方根误差以及希尔不等系，表明经过该组合模型预测的结果具有较高可信度，其结果对武汉市未来的土地利用规划工作具有一定的参考价值。

参考文献：

[1]徐晓雨.城市建设用地规模增长的驱动力分析——以武汉市为例[D].武汉：华中农业大学,2010.

[2]张晓东,阳亮.交通能源需求量组合预测模型研究[J].南京工程学院学报,2008,6(2):62-67.

[3]BATES T M,GRANGER C M J.The Combination of Forecasts[J].Operational Research Society,1969,20(4)：451-468.

[4]邱道持,刘力,粟辉,等.城镇建设用地预测方法新探——以重庆市渝北区为例[J].西南师范大学学报,2004,29(1):146-150.

[5]由向平,孙德山,林丹凤.组合模型在我国GDP预测中的应用[J].廊坊师范学院学报,2010,10(2):87-89.

[6]刘纪远,张增祥,徐新良,等.21世纪初中国土地利用变化的空间格局与驱动力分析[J].地理学报,2009,64(12):1411-1420.

[7]涂建军,廖和平,刘力,等.城镇建设用地双因素预测模型的改进——兼论城镇人口的预测方法[J].西南师范大学学报,2005,30(2):354-357.

[8]邵建英,王珂,肖志豪,等.城镇建设用地预测方法研究[J].江西农业大学学报,2006,28(3):472-476.

引文格式：孟成，彭明军，潘琛玲，等. 基于最小二乘原理的组合模型在建设用地需求量预测中的应用[J].测绘通报，2015(3)：111-114.DOI:10.13474/j.cnki.11-2246.2015.0091

作者简介：孟成(1985—)，男，博士，主要从事GIS方面的研究工作。E-mail： mengcheng@foxmail.com

基金项目：国家“十二五”科技支撑计划(2012BAH24B00)