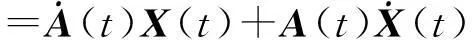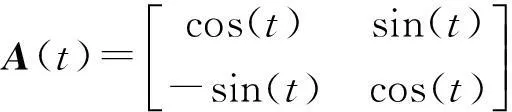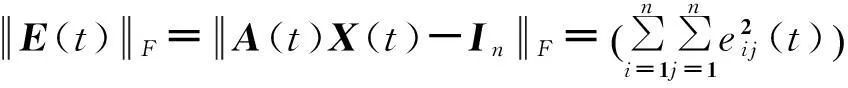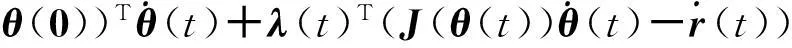终态神经计算：有限时间收敛性与相关应用

孙明轩，余轩峰，孔　颖

(浙江工业大学 信息工程学院，浙江 杭州 310023)

终态神经计算：有限时间收敛性与相关应用

孙明轩，余轩峰，孔颖

(浙江工业大学 信息工程学院，浙江 杭州 310023)

摘要：为了改进动态神经网络的收敛性能，引入终态吸引概念，提出终态神经网络及终态计算方法.对矩阵微分方程的终态吸引性进行分析，结果表明：该方法可保证网络有限时间收敛于零.终态神经网络可应用于求解时变矩阵求逆以及冗余机械臂的轨迹规划，仿真算例针对一平面机械臂，末端执行器完成一个封闭轨迹后，关节角回到初始位置，实现可重复运动.仿真结果验证了终态神经网络方法的有效性.

关键词：有限时间收敛；神经网络；时变矩阵；冗余机械臂；轨迹规划

Terminal neural computing：finite-time convergence

and the related applications

SUN Mingxuan, YU Xuanfeng, KONG Ying

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:This paper suggests the use of terminal neural networks for computing, in order to improve the convergence performance of asymptotically convergent ones. The terminal attraction of the matrix differential equations are analyzed, and the results show that the method can ensure the networks converge to zero in finite time. The terminal neural networks can be applied to solving the time-varying matrix inversion and the trajectory planning of redundant manipulators. A simulation example for a planar manipulator, where the end-effector completes a closed path and the joint variables can return to their initial values, makes the motion repeatable. The simulation results verify the validity of the terminal neural network method.

Keywords:finite time convergence; neural networks; time-varying matrices; redundant manipulators; trajectory planning

矩阵方程求解是一类重要的矩阵分析与计算问题[1]，有着非常广泛的应用背景.因其串行处理的本质，目前已经提出的大量数值算法并非十分有效(特别当求解时变矩阵时).动态神经计算具有高速并行处理能力，能够实现实时计算[2-4]，特别是在处理时变矩阵问题时能达到较好的效果[5].机械臂的运动规划是机器人学中一个重要的课题[6-7].实际中，机械臂末端执行器除完成规定的任务,还需躲避障碍、回避关节极限等，冗余机械臂具有更多的自由度，其运动规划容易满足更多作业要求，可采用递归神经网络方法解决这样的冗余度解析问题[8-9].近年来，Zhang等[10]巧妙地提出了有效的动态神经网络方法，处理冗余机械臂的重复轨迹规划任务.

目前提出的动态神经网络方法多采用渐近动态特性，在时间趋于无穷时，其网络变量收敛于零.相比于渐近动态特性，终态收敛动态特性具有有限时间收敛性[11]，不仅能够改进收敛速度，而且可以提高收敛精度.Zak等[12]将终态吸引特性用作激活函数，提出了有限收敛神经网络，并用于解决时变矩阵计算问题[13].我们知道，通常的激活函数具有更广的应用背景.因此，笔者提出一种终态神经网络，其动态特性具有终态收敛性质，它的激活函数可以是通常的激活函数；并将其应用解决时变矩阵求逆与冗余机械臂的重复运动规划.主要工作包括：提出终态神经网络以及其加速形式；将终态神经网络方法应用于矩阵求逆；将终态神经网络方法应用于冗余机械臂重复运动规划.

1动态神经网络

首先，引入如下记法：对于时变矩阵A(t)=(Aij(t))∈Rn×n，Aij(·):R+→R为矩阵A(t)的第i行第j列的元素，1≤i,j≤n，记；为矩阵A(t)的导数，可表示为；为矩阵A(t)在区间[a,b]上的积分，并定义t.

考虑由下述矩阵微分方程描述的神经网络

(1)

其中：γ>0为可调整参数；E(t)∈Rn×n为时变矩阵；S(·):Rn×n→Rn×n为激活函数，定义为S(E(t))=S(Eij(t)).

-γEij(t)S(Eij(t))

其中⊙表示Hadamard积.因此，为了保证E(t)收敛性，须E(t)⊙S(E(t))是正定的[5].这样，任何严格单调增奇函数可作为激活函数，满足S(-·)=-S(·).应该指出的是，激活函数的不同选择会导致不同的收敛速率.

进一步地，考虑下述矩阵微分方程描述的神经网络

(2)

式中α>0.当α=1时，式(2)退化为式(1)所表示的动态系统；Li等[11-12]将(·)α作为一类激活函数，笔者则是将式(2)作为一类动态系统(实际上，它是终态吸引动态系统)，它的激活函数可以是通常的形式，且该形式下的激活函数具有更广的应用范围.

为了保证E(t)收敛性，须E(t)⊙S(Eα(t))是正定的.因此，激活函数S(·)仍可取严格单调递增奇函数，而幂次α的选择需按照以下取法：

1) 当E(t)≥Λ时，取α=q1/p1，q1和p1为正奇数，且满足q1≥p1.

2) 当E(t)<Λ时，取α=q2/p2，q2和p2为正奇数，且满足q2

这里，Λ为每个元素均取值1的矩阵.

下面给出更为一般形式的终态神经网络，即

(3)

式中：γ,α1,α2>0，q1和p1，q2和p2均为正奇数，满足q1≥p1，q2

为表述简洁起见，以下简单地将激活函数取作线性函数形式，即，S(E)=E；且仅考虑q1=p1，q2=q，p2=p的情形.关于通常形式激活函数的研究结果将另文发表.

2有限时间收敛性

取线性激活函数S(E)=E，式(1)所示神经网络的动态响应可表达为

E(t)=E(0)e-γt

(4)

由式(4)知：当t→∞，若E(0)≠0，则E(t)渐近收敛于0.因此，式(1)为渐近收敛的神经网络，称为渐近神经网络(简写为ANN).显然，ANN网络收敛至平衡态E(t)=0(即原点)需要无限长时间.

为了改进收敛速率，笔者通过引入终态吸引子，提出终态神经网络(简写为TNN)，能够实现有限时间收敛性能，下面给出具体的分析结果.考虑下述矩阵微分方程

(5)

其中：q和p为正奇数，且满足q

由式(5)知：

对上式进行积分

从而任意初始状态E(0)(>0)收敛于平衡态E(t)=0的时间为

(6)

由于引入了幂次q/p<1，右端函数在原点的导数为无穷大，越接近原点，E(t)的收敛速度越快.由式(6)知：终端时刻不但与所选取的参数有关，也与初值E(0)有关，E(0)越远离原点，终端时刻越长，然而，也因为幂次q/p<1，由式(5)描述的TNN，在远离原点时，其收敛速度甚至比ANN的收敛速度慢.为此，采用如下改进形式的TNN网络，即

(7)

其中：β1=γα1；β2=γα2.易知，β1>0，β2>0，这是式(3)的一种简单形式.

式(7)又可写成

(8)

记Y(t)=E1-q/p(t)，则

将式(8)代入，可得

(9)

求解一阶线性矩阵微分方程式(9),得

在时刻tf，令Y(tf)=0，则

这样，从任意初始状态E(0)(>0)到达平衡态E(t)=0所需的时间为

(10)

与式(6)相比较，适当设定β1，β2，p，q，可使网络在更短时间到达平衡态.当E(t)远离平衡点时，β1E(t)是决定收敛时间的主要影响因素，当E(t)接近平衡状态E(t)=0时，则β2Eq/p(t)变为主要影响因素.因此，TNN网络式(6)能够加速收敛，使得E(t)更快收敛.

3时变矩阵求逆

给定满秩的时变矩阵A(t)∈Rn×n，X*(t)∈Rn×n是A(t)的逆矩阵，即X*(t)=A-1(t)，t∈[0,+∞).由逆矩阵定义为

A(t)X*(t)=In

(11)

其中In为n×n单位矩阵.考虑矩阵求逆问题，X*(t)=A-1(t)为未知矩阵，对于每个固定的时刻t，可通过直接求解式(11)获得.

与梯度法不同，Zhang[5]提出动态神经网络方法，巧妙地解决了时变矩阵求逆问题，其中，动态网络如式(1)所描述.容易证明，当时间趋于无穷时，其网络状态收敛于零，进而，X(t)收敛于逆矩阵X*(t).利用前节所述终态神经网络解决时变矩阵求逆问题，经过有限时间，使得X(t)收敛于X*(t).

定义矩阵误差函数为

E(t)=A(t)X(t)-In

(12)

求取已知矩阵的逆矩阵的目的可表述为，选取适当的误差动态方程，使得误差E(t)收敛于0.特别地，采用终态神经网络方法，取式(5)所示的误差动态方程，它可进一步写成

(13)

同理，采用加速终态神经网络方法，取式(7)所示的误差动态方程，它又可写成

-γ(β1(A(t)X(t)-In)+β2(A(t)X(t)-In)q/p)

(14)

考虑如下时变矩阵

(15)

容易给出其逆矩阵

(16)

初始误差X(0)可任意选取，这里取作

应用两种终态神经网络方法，均能使X(t)收敛到逆矩阵的理论值，即A-1(t).同时，加速因子γ可加快收敛速度.为了便于与ANN方法进行比较，两种终态神经网络方法均采用相同的仿真数据.

1) 终态神经网络式(5)

采用终态神经网络式(5)，以式(13)构建如图1所示仿真模型.仿真中，取q=3，p=5.γ=1时，仿真结果如图2所示.从图2中可以看出：由给定的初态出发，X(t)均收敛于逆矩阵A-1(t)，图中显示了X(t)的四种状态X11，X12，X21和X22对应的实际值与期望值的对比曲线，且后文图中出现四种状态的地方代表的含义相同.图3所示为γ=10时的状态X(t)，显然，其收敛速率明显比γ=1时快.对于渐近神经网络在相同初态下进行仿真，获得的结果见图4，可以看出：由给定的初态出发，X(t)渐近收敛于逆矩阵A-1(t).

图1　以式(13)神经网络模型求解逆矩阵的框图Fig.1　The diagram of neural network module (13) for matrix inversion

图2　γ取1时的终态神经网络式(5)Fig.2　Terminal neural network (5) with γ=1

图3　γ取10时的终态神经网络式(5)Fig.3　Terminal neural network (5) with γ=10

图5　γ取不同值TNN和ANN的误差比较Fig.5　Comparison of error by using ANN and TNN (5) with different γ

2) 终态神经网络

图6　γ取1时的终态神经网络式(7)Fig.6　Terminal neural network (7) with γ=1

4冗余机械臂的重复运动规划

考虑笛卡尔空间机械臂终端轨迹m维向量r(t)和机械臂关节空间n维向量θ(t)，其关系可表示为

r(t)=f(θ(t))

(17)

映射关系式(17)是非线性的，且具有复杂的表达形式(特别是对于高自由度的机械臂).式(17)通常要转换成速度模式进行求解，转换后的关系可表示为

(18)

图7　γ取不同值时，三种神经网络误差比较Fig.7　Comparison of error by the three neural networks with different γ

针对冗余机械臂而言，对于给定的末端执行器的工作路径，实时计算所对应的关节向量可行路径的问题称为冗余机械臂的逆解运动学问题，由于其存在多余的自由度，因而该逆解问题存在无穷多组解，且能实现躲避障碍、躲避奇异点以及避免关节超限等.

充分考虑机械臂的冗余特性，已经提出了众多方案来求解该逆解运动学问题.其中，伪逆型方法是求解该问题的一种常用方法，该方法在求解过程中会考虑不同的最优标准，例如关节速度范数最小化和目标任务最优控制等.然而，该方法存在一些不足，例如，矩阵伪逆的高计算负荷会导致高计算复杂度，且伪逆型方法并不能实现机械臂的可重复运动.

对于冗余机械臂，式(18)可能存在多解或无穷多解.且由于伪逆方法求解式(18)存在的不足，使得末端执行器沿封闭路径运行并不能保证关节最终沿封闭路径运行，对于重复运动控制而言，这种形式的关节角初始偏移是不可接受的.

一般地，存在许多因素影响冗余机械臂的运动规划，例如末端执行器的运动需求，关节的物理限制等，这些因素使得当选取伪逆型方法求解机械臂逆解运动学问题时，并不能实现该运动学控制可重复(当末端执行器执行一个特殊任务时，不能使得机械臂的初始配置与最终配置相一致).

与常用的伪逆型求解方案不同，本小节引用了一种冗余机械臂的在线重复运动规划最优方案，该方案充分考虑伪逆型方法存在的缺陷，可以有效的解决一个运行周期结束关节角发生偏移的问题(关节角偏移是指当末端执行器跟踪一个闭环路径以后，关节变量并不能回到初始设定的值)，实现冗余机械臂的可重复运动.

为了使得关节能够重复运动，应使得关节的初态位置和当前位置之间的差最小，可利用的性能指标[9]为

(19)

其中：c=θ(t)-θ(0)，θ(0)为关节角的初始值；参数μ>0，用来引入当前关节角和初始关节角的差值的影响，且在硬件条件允许的前提下设计的越大越好(或者为了实现较理想的仿真效果应设计适当大小).这样，冗余机械臂运动规划任务可以表达为下述二次规划

(20)

W(t)y(t)=v(t)

(21)

其中

(22)

这里，I为具有相应维数单位矩阵，且

(23)

(24)

可以看出：应用拉格朗日乘子法，二次规划问题的求解变为式(21)的求解.所以采用同样的性能指标式(18)，是为了比较终态神经网络与渐近神经网络在同时应用于所述规划问题时的求解效果.

下面分别利用ANN和TNN神经网络进行三连杆平面机械臂的运动规划.雅可比矩阵为

其中

B=2πcos(0.5πt/T)cos(0.5πt/T)

图8　三连杆平面机械臂的沿圆路径轨迹Fig.8　Trajectories of the three-link planar robot arm when its end-effector tracking an circular path

运行结果见图8~11所示.图8为三连杆平面机械臂在二维平面中的运动轨迹，它按照逆时针方向运动，且起始位置正好是该圆轨迹的最右端.这里只给出了TNN模型下的关节和终端轨迹.由仿真结果知：实际轨迹与期望轨迹的误差为10-3数量级.图9，10所示的是TNN模型下机械臂关节角和关节角速度在一个周期内的变化情况.ANN模型下的三个关节角度和速度归零的精度分别为10-3和10-4数量级，而TNN模型下为10-4和10-5数量级.图11为ANN和TNN模型下E(t)在一个周期内的变化，从图11中可以看出：使用终态神经网络方法，E(t)的收敛速度明显变快了，同时收敛精度也较高，可达10-7，而使用ANN方法收敛精度则为10-6.仿真结果表明了所提TNN方法是有效的.

图9　使用终态神经网络时关节角在一个周期内的变化Fig.9　Joint angles during a period when using the terminal neural network model

图10　使用终态神经网络方法时关节角速度在一个周期内的变化Fig.10　Joint velocities during a period when using the terminal neural network model

图11　使用两种不同的神经网络时E(t)在一个周期内的变化Fig.11　The E(t) during a period when using both ANN and TNN (5) neural networks models

5结论

依照动态神经网络方法，引入终态吸引概念，笔者提出了终态神经网络方法，它可使得网络变量有限时间收敛于零.在终端动态方程中增加一附加项，使得网络收敛速度得到进一步提高.与渐近网络相比，收敛速度和精度两方面均得到改善.终态神经网络方法可应用于矩阵求逆和二次规划问题，并给出了具体仿真算例.数值结果验证了终态神经网络求解矩阵求逆和二次规划问题的有效性.

参考文献：

[1]HORN R A, JOHNSON C R. Topics in matrix analysis[M].

England：Cambridge University Press,1991.

[2]WANG Jun. Electronic realisation of recurrent neural work for solving simultaneous linear equations[J]. Electronics Letters,1992,28(5)：493-495.

[3]WANG Jun. Analysis and design of a recurrent neural networks for linear programming[J]. IEEE Transactions on Circuits and Systems,1993,40(9)：613-618.

[4]WANG Jun. Recurrent neural networks for computing pseudoinverses of rank-deficient matrices[J]. SIAM Journal on Scientific Computing,1997,18(5)：1479-1493.

[5]ZHANG Yunong, GE Shuzhi. Design and analysis of a general recurrent neural network model for time-varying matrix inversion[J]. IEEE Transactions on Neural Networks,2005,16(6)：1477-1490.

[6]WHITNEY D E. Resolved motion rate control of manipulators and human prostheses[J]. IEEE Transactions on Man Machine Systems,1969,10(2)：467-53.

[7]徐建明,张健,吴世民,等.基于ARM的机械手运动控制系统设计[J].浙江工业大学学报,2014,42(3)：243-248.

[8]WANG Jun, HU Qingni, JIANG Danchi. Lagrangian network for kinematic control of redundant robot manipulators[J]. IEEE Transactions on Neural Networks,1999,10(5)：1123-1132.

[9]XIA Youshen, WANG Jun. A dual neural network for kinematic control of redundant robot manipulators[J]. IEEE Transactions on Systems, Man, and Cybernetics,2001,31(1)：147-154.

[10]ZHANG Yunong, ZHANG Zhijun. Repetitive motion planning and control of redundant robot manipulators[M]. Germany：Springer Berlin Heidelberg,2013.

[11]LI Shuai, LI Yangming, WANG Zheng. A class of finite-time dual neural networks for solving quadratic programming problems and its k-winners-take-all application[J]. Neural Networks,2013(39)：27-39.

[12]ZAK M. Terminal attractors for addressable memory in neural networks[J]. Physics Letters A,1988,133(1)：18-22.

[13]LI Shuai, CHEN Sanfang, LIU Bo. Accelerating a recurrent neural network to finite-time convergence for solving time-varying Sylvester equation by using a sign-bi-power activation function[J]. Neural Processing Letters,2013,37(2)：189-205.

(责任编辑：刘岩)

中图分类号：TP13

文献标志码：A

文章编号：1006-4303(2015)03-0311-07

作者简介：孙明轩(1962—)，男，安徽固镇人，教授，博士，研究方向为学习控制，E-mail：mxsun@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(60874041,61174034)

收稿日期：2014-12-23