湍流模型在折流板换热器壳侧结构优化中的应用

汤　亮,叶方平,龚发云,钱　坤

(湖北工业大学 机械工程学院,湖北 武汉　430068)



湍流模型在折流板换热器壳侧结构优化中的应用

汤亮,叶方平*,龚发云,钱坤

(湖北工业大学 机械工程学院,湖北 武汉430068)

摘要:研究不同湍流模型在换热器流场和传热计算中的适用性,分别采用Spalart-Allmaras湍流模型、标准k-ε湍流模型和可实现k-ε湍流模型计算换热器在不同入口速度下的出口温度、换热系数等参数．将3种湍流模型的CFD计算结果与Bell-Delaware理论计算值进行对比可知,Spalart-Allmaras湍流模型的换热器性能数值计算存在明显缺陷,可实现k-ε湍流模型的换热器CFD较其他两种湍流模型的更为适用．将适用性较好的可实现k-ε湍流模型进行CFD数值模拟,模拟结果表明挡切率为25%时换热器性能最佳．

关键词:湍流模型;CFD;换热器;结构优化

管壳式换热器具有结构简单牢固、操作弹性大、应用材料广等优点,广泛用于化工、石油和能源系统．目前换热技术正在从大型化向微小化发展,小尺寸管壳式换热器的应用比较广泛[1-2]．评价换热器性能优劣的参数较多,如传热系数、换热面积、压降等[3]．但换热器内部的流动与换热情况很难观测到,且壳侧内部的流场分布、温度分布和传热系数会直接影响到换热器的性能,结构优化也成为换热器研究的热门[4]．在对换热器壳程流动和传热的计算流体动力学(computational fluid dynamics,简称CFD)的预测中,数值计算模型必须考虑到相关结构的综合作用,才能更精确地预测换热器壳程流动和传热[5]．现在很多研究中都讨论了不同湍流模型对具体对象的适用性.黄胜等[6]研究了不同湍流模型在螺旋桨水动力性能预报中的适用性．包涵龄等[7]研究了机翼气流分离区的预测方法和不同湍流模型对其预测结果的影响．为了考察不同湍流模型对换热器壳程流动和传热的适用性,作者采用不同的湍流模型对换热器流场的分布、温度的分布和传热系数进行研究,并将不同湍流模型下的CFD计算值和Bell-Delaware理论计算值[8]进行对比,评估湍流模型对小型折流板换热器的适用性,并应用合适的湍流模型对此换热器在不同挡切率和挡板间距情况下的流场进行分析,得到对应的最优结构参数．

1控制方程

1.1　质量守恒方程

质量守恒定律可以表述为:单位时间内流体微元体中质量的增加等于同一时间内流入该微元体的净质量．按照这一定律,可以得出质量守恒方程[9]为

(1)

1.2　动量守恒方程

动量守恒定律可描述为:对于一个给定的流体微元体,其动量对时间的变化率等于外界作用在该微元体上的各种力之和．依据这一定律,X,Y,Z方向动量方程为[9]

(2)

(3)

(4)

其中:p为流体微元体上的压强;τxx、τxy、τxz等是因分子粘性作用而产生的作用在微元体表面上的粘性应力τ的分量;fx、fy、fz为3个方向的单位质量力,若质量力只受重力,且Z轴垂直向上,则fx=fy=0,fz=-g．

1.3　能量守恒方程

能量守恒方程是有热交换的流动系统必须满足的基本定律,可表述为:微元体中能量的增加率等于进入微元体的净热流量加上体力和面力对微元体所做的功．按照这一定律,可以得到以温度T为变量的能量守恒方程[9]

(5)

其中:Cp为比热容;T为温度;λ为流体的导热系数;ST为粘性耗散项,即流体的内热源及由于粘性作用流体机械能转换为热能的部分．

2湍流模型

由于在此研究中的流动是湍流,湍流效应应该使用湍流模型．常用的湍流模型有单方程模型、标准k-ε模型、重整化群k-ε模型、可实现k-ε模型、雷诺应力模型[10]．

2.1　Spalart-Allmaras湍流模型

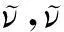
(6)

2.2　标准k-ε湍流模型

标准k-ε湍流模型中液相湍动能方程和耗散率方程[9]可分别表示如下

(7)

(8)

其中:k为湍动能;ε为耗散率;μt为湍流粘性系数;Gk为由平均速度梯度引起的湍动能增量．

μt和Gk的表达式为

(9)

(10)

其中:c1=1.44;c2=1.92;cμ=0.99;σk和σε分别为湍动能和湍流耗散率对应的普朗特常数,σk=1.0,σε=1.33．

2.3　可实现k-ε湍流模型

因为对于时均应变率特别大的情形,标准k-ε湍流模型有可能导致负的正应力．为使流动符合湍流的物理定律,需要对正应力进行某种数学约束．可实现k-ε湍流模型正是基于这种原理提出的,其湍动能及耗散率运输方程[9]分别为

(11)

(12)

其中:Gk是由于平均速度梯度引起的湍动能;Gb是由于浮力影响引起的湍动能;YM是可压缩湍流的过度扩散产生的湍动能变化;C1ε=1.44、C3ε=0.09、C2=1.9、σk=1.0、σε=1.2．

3计算模型

作者构建一个小尺寸管壳式折流板换热器,换热器主要由管壳和多根列管组成,壳体与折流板之间无间隙,折流板与管束之间无间隙.表1为换热器有关参量．

表1　换热器的有关参量

4边界条件及网格划分

流场使用基于有限元体积法的3维单精度Fluent求解软件进行数值模拟,选择基于压力的半隐式求解方式,在求解参数的过程中流动方程(flow)、湍流方程(turbulence)和能量方程的离散计算格式均采用2阶迎风格式(second order upwind)．3维几何模型使用正交六面体网格进行划分,进口速度大小为0.5 m·s-1,温度为298 K,换热管壁温度为378 K．

5结果与讨论

5.1　不同湍流模型下壳程换热情况分析

在前文建立的换热器模型下,选择4种不同的湍流模型,设置4种入口速度为0.5、1、1.5、2 m·s-1,计算得到不同入口速度下换热器的出口温度．图1为不同湍流模型下入口速度与出口平均温度之间的关系.从图1可知,在换热器出口平均温度随入口速度变化的趋势方面,Spalart-Allmaras湍流模型与标准k-ε湍流模型和可实现k-ε湍流模型的变化趋势恰恰相反,而且根据换热规律,随着入口速度的增加,出口温度应该是下降的,因此Spalart-Allmaras湍流模型不适合此换热器的CFD分析．

对于壳程换热系数的计算采用Bell-Delaware法[10]．Bell-Delaware法是Bell以1963年Colburn等人完成的Delaware研究成果为基础,提出的一种精确度较高的半理论方法,此方法利用大量实验数据,引入了各流路的校正系数,考虑了传热、流动与结构的综合效应[11-12]．图2a和图2b分别为可实现k-ε湍流模型与标准k-ε湍流模型下换热器的总换热功率随入口速度的变化情况.从图2可以看出,在可实现k-ε湍流模型下CFD分析值与Bell-Delaware法得到的变化趋势相同,总的换热功率值也很接近;而在标准k-ε湍流模型下CFD分析值与Bell-Delaware法得到的变化趋势虽然相同,但总的换热功率相差较大．由此得出可实现k-ε湍流模型较为适合此换热器的CFD分析．

5.2　不同挡切率和间距下换热器流场CFD分析

在计算折流板挡切率和间距变化对换热器性能影响的过程中,以折流板挡切率和间距作为变量,挡切率分别取25%和36%,折流板数目分别取6、8、10、12,换热器进口速度取为0.5 m·s-1．图3、4分别为挡切率为36%和25%时不同折流板数目下的换热器内部流体轨迹线．从图3、4可以看出,随着折流板挡切率的减小,折流板的阻挡作用增强,流体流通的主流区域集中于折流板窗口的纵向延伸方向,流体流向改变的位置愈接近下一个折流板,同时回流区也逐渐增大,即回流区管壁的传热没有被有效地利用,主流区流速大大高于其他区域流速,流速分布的不均匀性更加突出．当流体通过切口时有部分流体被截留下来形成回流,挡切率较大时,截留下来的流体少一些;挡切率较小时,被截留的流体多一些,且流体的速度冲量也更大,从而形成的回流漩涡也大一些．

换热器壳程换热性能由多种因素决定,换热量和压力损失是衡量换热器性能的重要指标,但是从优化设计的角度出发,单独通过任何一个参量来确定换热器整体性能的优劣显然是不可取的．目前国内外使用较多的处理方法是以单位压力损失下换热系数的大小作为衡量标准,来综合评估换热器的整体性能．以可实现k-ε湍流模型下入口速度0.5 m·s-1为例进行计算,图5a为壳程总换热功率与折流板数目之间的关系,从图5a可以看出,随着折流板数量的增加,壳程总换热功率随之增加,挡切率为25% 的壳程总换热功率始终比挡切率为36%时要高．图5b为单位压力损失下换热系数的大小与折流板数目之间的关系,从图5b可以看出,挡切率为25%的换热器的换热效果始终高于挡切率为36%的情况,即挡切率为25%时此换热器的性能较好．

6结束语

(1) Spalart-Allmaras湍流模型对换热器性能的数值计算存在明显的缺陷,表明该模型不适合模拟计算小尺寸换热器壳程的流动;

(2) 通过对总换热功率的考察,可实现k-ε湍流模型下的CFD计算与Bell-Delaware法的值最为接近,因此可实现k-ε湍流模型具有较其他两种模型更强的数值模拟能力;

(3) 随着折流板挡切率的减小,流体流通的主流区域集中于折流板窗口的纵向延伸方向,流体流向改变的位置愈接近下一个折流板,同时回流区也逐渐增大,即回流区管壁的传热没有被有效利用,主流区流速大大高于其他区域流速,流速分布的不均匀性更加突出;

(4) 以适用性较好的可实现k-ε湍流模型进行CFD计算,评估在两种挡切率的情况下的相关数据,可知挡切率为25%时，换热器的性能最佳．

参考文献：

[1]钱颂文.换热器设计手册[M].北京:化学工业出版社,2002.

[2]王元文.管壳式换热器的优化设计[J].广东化工,2005(3):43-44.

[3]罗贻乡.管式换热器的优化设计[J].石油机械,2005,27(9):14-15.

[4]刘敏珊,董其伍,刘乾.折流板换热器壳程流场数值模拟与结构优化[J].化工设备与管道,2006,2(43):24-31.

[5]李雪英,任静,蒋洪德.不同湍流模型对叶栅对流传热预测的影响[J].工程热物理学报,2013,34(6):1043-1046.

[6]黄胜,王超,王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J].哈尔滨工程大学学报,2009,30(5):481-485.

[7]包涵龄,陈鹏,武玉英.用不同湍流模型预测机翼边界层分离区[J].北京工业大学学报,2003,29(2):159-163.

[8]Kakac S,Bergles A E,Mayinger F. Heat exchangers: thermal-hydraulic fundamentals and design[M]. New York: Hemisphere,1981.

[9]张建文,杨振亚,张政.流体流动与传热过程的数值模拟基础与应用[M]. 北京: 化工工业出版社,2008.

[10]谷俊.管壳式燃滑油散热器换热特性计算方法及试验验证[J].航空发动机,2013,39(1):65-69.

[11]马小明.管壳式换热器[M].北京:中国石化出版社,2010.

[12]Sunden B.Computational fluid dynamics in research and design of heat exchangers[J].Heat Transfer Ehg,2007,24,898-910.

(责任编辑郑小虎)

Application of turbulence model in baffle heat exchanger shell

side structural optimization

TANG Liang,YE Fang-ping*,GONG Fa-yun,QIAN Kun

(School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China)

Abstract:Different turbulence models in the flow field of heat exchanger and heat transfer calculations applicability had been researched.In order to calculate the equation of the parameters at different heat exchanger outlet temperature of the inlet velocity, heat transfer coefficient Spalart-Allmaras turbulence model and the standard k-ε model and realizable k-ε model were used respectively．The comparison of 3 kind models between CFD calculations of turbulence model and the theoretical calculations of Bell-Delaware indicated that Spalart-Allmaras one equation turbulence model had flaw in the numerical calculation of heat exchanger performance.The realizable k-ε turbulence model equation was more applicable to CFD simulation of heat exchangers by comparing to other two turbulence models. Authors used the realizable k-ε turbulence model for simulation.The simulation results showed that the heat exchanger performed best when the baffle cut was 25%.

Key words:turbulence model;CFD;heat exchanger;structural optimization

通信作者

作者简介：杨莲(1988-)，女，新疆伊犁人，新疆大学硕士研究生；*帕孜来·马合木提()，新疆大学副教授，硕士生导师，E-mail: princeleesmile@sina.cn.

基金项目:国家自然科学基金资助项目(61364010)

收稿日期：2014-08-10

doi:10.3969/j.issn.1000-2162.2015.02.012

中图分类号：TK17

文献标志码:A

文章编号:1000-2162(2015)02-0062-06