螺旋屈曲钻柱中诱发扭矩计算方法的研究

廖振武， 徐健， 鄢标， 蒋国彪， 孙巧雷

（长江大学 机械工程学院，湖北 荆州 434023）

0 引 言

在钻井作业中，钻柱的螺旋屈曲问题一直是石油钻井行业的一个热点问题。螺旋屈曲的概念最早由Lubinski等［1］提出，他们是在忽略管柱自身重量与井壁摩擦的情况下，利用能量法求出螺旋屈曲的解析解，这种研究方法忽略了摩擦和钻柱自重，且认为钻柱发生螺旋屈曲时处在弹性变形的情况下，所以在钻柱中不会产生扭矩。

但是随着水平井和大位移井的增多，自重和摩擦是无法忽略的，传统的螺旋屈曲钻柱的强度安全性的分析方法明显不足。Mitchell［2］在考虑以上因素的情况下，进行了螺旋屈曲细长梁的水平大位移分析，他的研究显示在没有外加作用扭矩的情况下，螺旋屈曲钻柱中会产生诱发扭矩。并且一旦外加了屈曲力，钻柱中的扭矩平衡就被打破，同时由于钻柱的形状由正弦形变为螺旋形，扭矩会得到大幅度增加。为分析真实工况下螺旋屈曲管柱的强度安全性，必须对螺旋屈曲管柱中的诱发扭矩计算方法展开研究。

1 螺旋屈曲管柱诱发扭矩的计算模型描述

取钻柱中一段微小单元为研究对象，假设钻柱发生弹性形变，各段材料均匀。水平井造斜部分钻柱可能会发生一定角度的偏转，研究对象为微小单元，可以认定微小单元钻柱始终为圆 柱［3］。 基 于以上 假设可以把产生螺旋屈曲的钻柱简化成由弹性线形成的圆柱螺旋线，如图1所示。

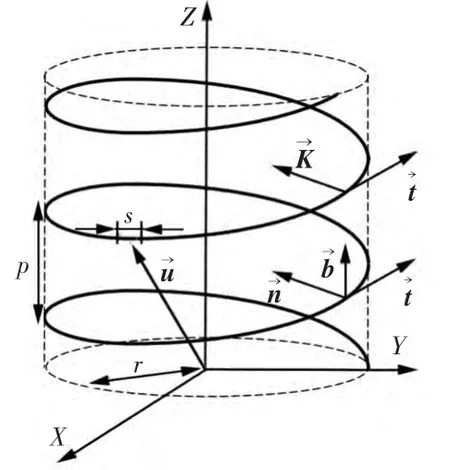
图1 螺旋屈曲管柱的力学分析模型

2 诱发扭矩计算方法的推导

在建立的空间坐标系中，圆柱螺旋线中任意一段弧长s可表示为

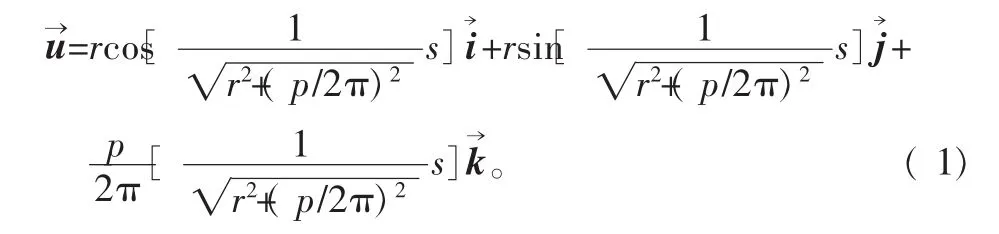
对于整段弹性管柱，认为其抗弯刚度EI是均匀不变的，用M表示钻柱中的诱发扭矩，则内外力矩平衡的欧拉-伯努利方程为

对于图1中的圆柱螺旋空间曲线有以下关系：

综合式（ 2）、（ 3）、（ 4）可得到

式（5）中圆柱螺旋空间曲线的正切向量是

空间曲线的曲率向量是

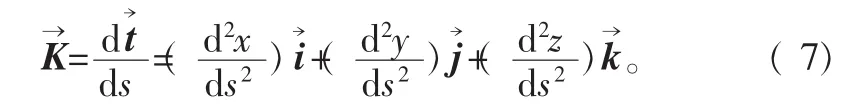
在实际钻井中，发生螺旋屈曲的钻柱和图1中的圆柱螺旋线有所不同，钻柱和井眼之间的半径间隙r与由管柱形成的螺旋线螺距相比是很小的［4］，即 p＞＞r。 因此弹性线与Z轴的偏差是较小的，可以假设d z≅d s。

在式（6）和式（7）中可以用d z替换d s，可以得到：

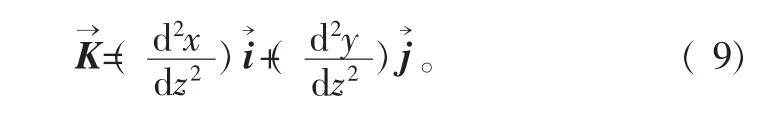
把式（8）和式（ 9）代入式（5），可以得到

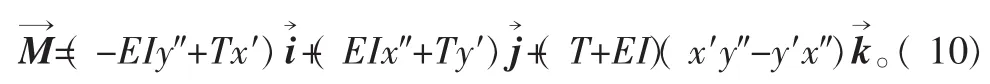
从式（10）可以得到各轴的扭矩是：

利用式（1）和假设条件d z≅d s，可以得到：

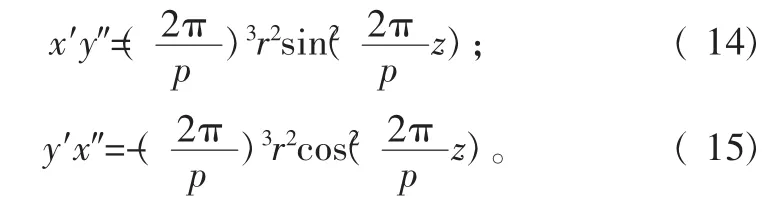
假设在式（13）中没有外部的扭矩被加载到钻柱的Z轴上（Mz=0），然后把式（ 15）和式（ 14）代入式（ 13），管柱内部的扭矩可由下式表达：

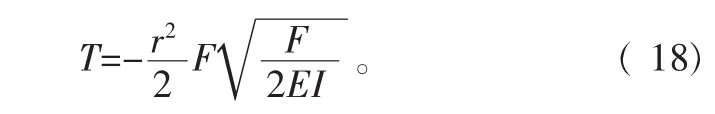
这样就得到了螺旋屈曲钻柱中诱发扭矩T的计算方法。

3 结 语

1）该算法能够对螺旋屈曲钻柱中的诱发扭矩进行计算，且适用于目前日益增多的水平井中；

2）该诱发扭矩计算公式能够反映诱发扭矩与轴向力、钻柱抗弯刚度和螺旋半径之间的线性关系，很好地弥补了现有的螺旋屈曲钻柱的强度安全性分析方法的不足；

3）这种诱发扭矩的计算方法是基于对钻柱的静力学分析，钻柱在实际工作时工况条件比较复杂，尚未考虑钻柱的振动，在下一步研究中可以把这些因素考虑进去。

而Lubinski所推导的螺旋屈曲管柱中轴向力和螺距的关系表达式为

由式（17）和式（16），在没有外加扭矩的情况下，螺旋屈曲诱发的扭矩T可由轴向力F表达，即

［ 1］ Lubinski A，Althouse W S，Logan JL.Helical buckling of tubing sealed in packers ［ J］.Journal of Petroleum Technology，1962（ 6）∶655-670.

［ 2］ Mitchell R F.The Twist and Shear of Helically Buckled Pipe［ J］.SPE Drilling&Completion，2004，19（ 1）∶20-28.

［3］ 徐春铃，王鑫伟.水平井眼中钻柱的螺旋屈曲分析［J］.机械科学与技术，2011（ 11）∶1927-1929，1933.

［4］ 刘殿福，林元华，甘燕芬，等.斜直井钻柱螺旋屈曲时轴向力钻速和井斜角间的关系［ J］.石油矿场机械，2007（ 12）∶30-33.

［5］ 胡华，夏辉，窦益华.定向井造斜段管柱屈曲分析［J］.内蒙古石油化工，2011（17）∶18-20.