电缆PVC绝缘层高温压力试验结果的不确定度评估

陈 鼎

(上海出入境检验检疫局机电产品检测技术中心，上海200135)

0 引言

高温压力试验的结果是用来考核电线电缆绝缘层或护套层材料重要的安全性能指标。进行该试验的目的是通过模拟电缆处于高温和机械压力双重作用下的情况，从而检验其绝缘层在高温下抵抗外力破坏的能力。根据以往检测经验可知，该试验过程步骤较复杂，涉及多种仪器装置操作，且对试验过程中环境温度和人员操作也有较高要求。为了对电缆绝缘材料性能做出恰当的评价，有必要对该试验结果进行测量不确定度评估。

1 概述

1.1 测量依据

GB/T 2951.31—2008/IEC 60811-3-1:1985《电缆和光缆绝缘和护套材料通用试验方法 第31部分:聚氯乙烯混合料专用试验方法——高温压力试验——抗开裂试验》。

1.2 评定依据

JJF 1059.1—2012《测量不确定度评定与表示》。

1.3 测量环境

环境温度:(23±5)℃;相对湿度:45%～75%。

1.4 测量仪器

(1)DMS-C17型高温压力试验装置:(0.70±0.01)mm;

(2)VMS-2515F型影像测量仪:30～190倍，±0.001 mm;

(3)SD202-2B型压力通风烘箱:0～200℃，±2℃;

(4)EA60FEG-1型电子天平:0～60 kg，±1%。

1.5 测量对象

一般用途单芯硬导体无护套电缆(60227 IEC 01(BV)4 mm2)，其绝缘层材料为聚氯乙烯(PVC)。

1.6 测量过程

在成品电缆样品上截取长度约为300 mm的样品段，将其均分成100 mm的3段，作为高温压力试验的3个试样，然后用影像测量仪测量出3个试样的外径和绝缘厚度，并计算其平均值，随后按式(1)得出计算压力值。

由GB/T 2951.31—2008标准规定，刀片作用于试样上的压力F计算公式为:

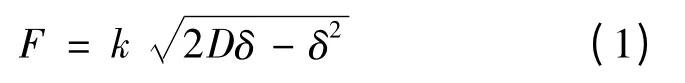
式中:F为计算压力;k为系数，当D≤15 mm时取0.6，D＞15 mm时取0.7;δ为绝缘试样厚度平均值;D为试样外径平均值。

δ和D均以mm计，到小数点后1位，按标准GB/T 2951.31—2008规定的方法，在试样端头切取的绝缘薄片上测得;F单位为N，可以向较小值化整，但舍去值不超过3%。

用高温压力试验装置沿垂直于试样轴向施加计算压力，刀口应与试样轴向垂直。将装好试样的试验装置整体放入压力通风烘箱中，在烘箱温度(80±2)℃下放置4 h。

加热结束后，用标准规定的方法迅速冷却试样后，抽出导体得到绝缘管状试件，立即进行压痕深度测量。压痕深度测量方法如图1所示，在压痕处和压痕附近横向切取2个绝缘试片剖面，剖面1和剖面2，压痕深度应为这2个剖面的测量值之差，以mm计，精确到2位小数。

图1 压痕深度测量方法示意图

实际测量时，在VMS-2515F型影像测量仪下观测到的绝缘试件剖面分别见图2、图3。

图2 观察到的压痕处绝缘试件

图3 观察到的压痕附近绝缘试件

将测得的3个试样的压痕深度结果的中间值与其绝缘厚度平均值的比值作为最终结果，以%计，精确到1位小数。

2 数学模型

根据GB/T 2951.31—2008标准规定的测试结果表示法，测试结果y为压痕深度与该试样绝缘平均厚度的比值。

式中:x为压痕深度;δ为绝缘平均厚度。

在实际试验中，测试结果与施加的压力、烘箱温度以及刀口宽度有关，故在测量不确定度评定中必须考虑这三个附加因素的影响。

根据以往试验经验，压力和温度对试验结果影响的大小基本上与被测量压痕深度的大小成正比，而刀口宽度对结果影响的大小基本上与压痕深度的大小成反比，因此在式(2)中加入这些影响量后，建立数学模型为:

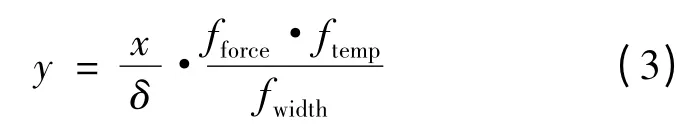
式中:fforce为由施加压力对测试结果的影响所引入的修正因子;ftemp为由烘箱温度对测试结果的影响所引入的修正因子;fwidth为由刀口宽度对测试结果的影响所引入的修正因子。

上述三个因子的数学期望均等于1。即

由于该模型仅包含输入量的商，故测试结果y的相对合成方差为:

即得到下式

3 测量不确定度分量

表1给出了各试件的测量结果汇总表。

表1 各试件测试结果汇总表

从同一电缆产品上截取的5个样品的重复试验结果，每个样品的3个试样的压痕深度中间值和对应的绝缘平均厚度如表2所示。

表2 同一产品5个样品的重复测量结果(单位:mm)

3.1 压痕深度的相对不确定度urel(x)

影响压痕深度测量结果的主要因素:重复性、仪器误差、环境温度波动和人员操作。

(1)重复性测量引入的不确定度u1(x)

如表2，有5个样品，每个样品分成3个试样，取3个试样压痕深度的中间值作为测量结果。用极差法可得由重复性引入的不确定度为:

(2)影像测量仪示值误差导致的不确定度u2(x)

已知VMS－2515F型影像测量仪的最大允许误差MPE=±0.001 mm，则其概率密度分布区间的半宽为0.001 mm。

由测量仪器的最大允许误差导致的不确定度可近似地估计为矩形分布，故包含因子取k=。

因此，仪器误差导致的不确定度分量为:

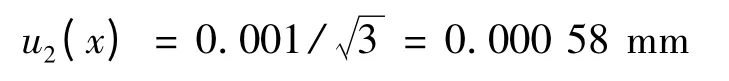
(3)环境温度变动导致的不确定度u3(x)

已知实验室环境温度为(23±5)℃，即实验室内的温度在Δt=±5℃范围内变动。由于绝缘厚度测量属于线测量，温度变动对线测量的影响可以通过线热膨胀系数来进行计算。经查热膨胀系数表，可知样品电缆绝缘层所用的PVC材料的线热膨胀系数α=80.0×10－6℃－1，于是环境温度变动导致的不确定度分量为:

(4)人员操作导致的不确定度u4(x)

人员操作导致的不确定度在这主要指在制备试样和使用仪器的过程中引入的不确定度。根据经验估计，人员操作引入的测量误差在±0.01 mm范围内，以矩形分布估计，则人员引入的不确定度分量为:

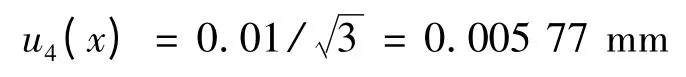
故合成上述各4个分量得:

以相对不确定度表示，则为:

3.2 绝缘平均厚度的相对不确定度uret(δ)

与压痕深度测量相同，影响绝缘厚度测量结果的主要因素:重复性测量、仪器误差、环境温度波动和人员操作。

(1)测量重复性引入的不确定度u1(δ)

如表2所示，取压痕深度中间值所对应的绝缘平均厚度，用极差法可得由重复性引入的不确定度为:

(2)影像测量仪示值误差导致的不确定度u2(δ)

由于绝缘厚度测量与压痕深度测量使用的是同一台影像测量仪，故仪器误差导致的不确定度分量为:

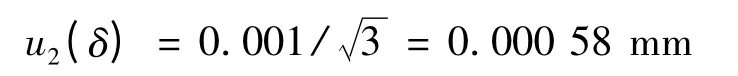
(3)环境温度变动导致的不确定度u3(δ)

已知实验室环境温度在Δt=±5℃范围内变动，于是环境温度变动导致的不确定度分量为:

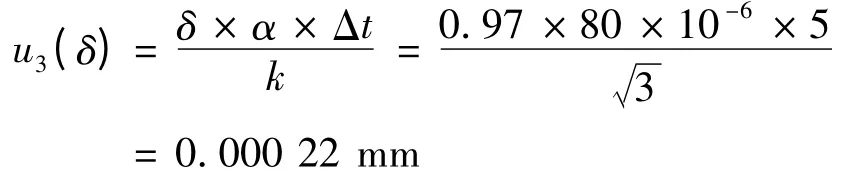
(4)人员操作导致的不确定度u4(δ)

根据经验估计，人员操作导致的不确定度在±0.01 mm范围内，以矩形分布估计，则人员引入的不确定度分量为:

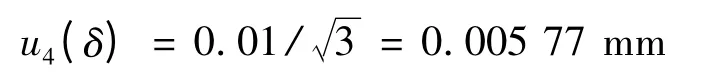
四者合成后，得绝缘平均厚度的标准不确定度为:

以相对不确定度表示，则为:

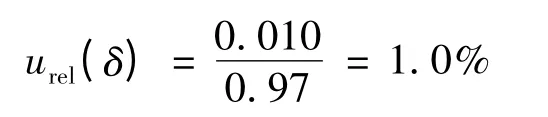
3.3 施加压力影响导致的相对不确定度urel(fforce)

实际试验中，计算压力F将被换算成对应质量的砝码，砝码在使用前需在电子天平上测量其实际质量m，因此电子天平的示值误差对实际施加的压力大小将产生主要影响。

已知EA60FEG-1型电子天平最大允许误差为±1%，故天平误差导致的不确定度分量为:

3.4 烘箱温度影响导致的相对不确定度urel(ftemp)

已知PVC材料的线热膨胀系数α=80.0×10－6℃－1，且SD202-2B型压力通风烘箱的温度在Δt=±2℃范围内变动，于是烘箱温度变动导致的不确定度分量为:

3.5 刀口宽度影响导致的相对不确定度urel(fwidth)

由于刀口宽度的大小直接影响刀片与绝缘试件的接触面积，即绝缘试件的受力面积，从而影响刀片对试件的压强。已知DMS-C17型高温压力试验装置的刀片宽度为0.70 mm，最大允许偏差为±0.01 mm，相当于±1.4%，于是刀口宽度偏差导致的不确定度分量为:

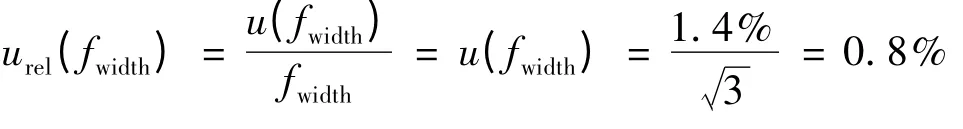
4 不确定度概算

表3给出了测量不确定度分量的汇总表。

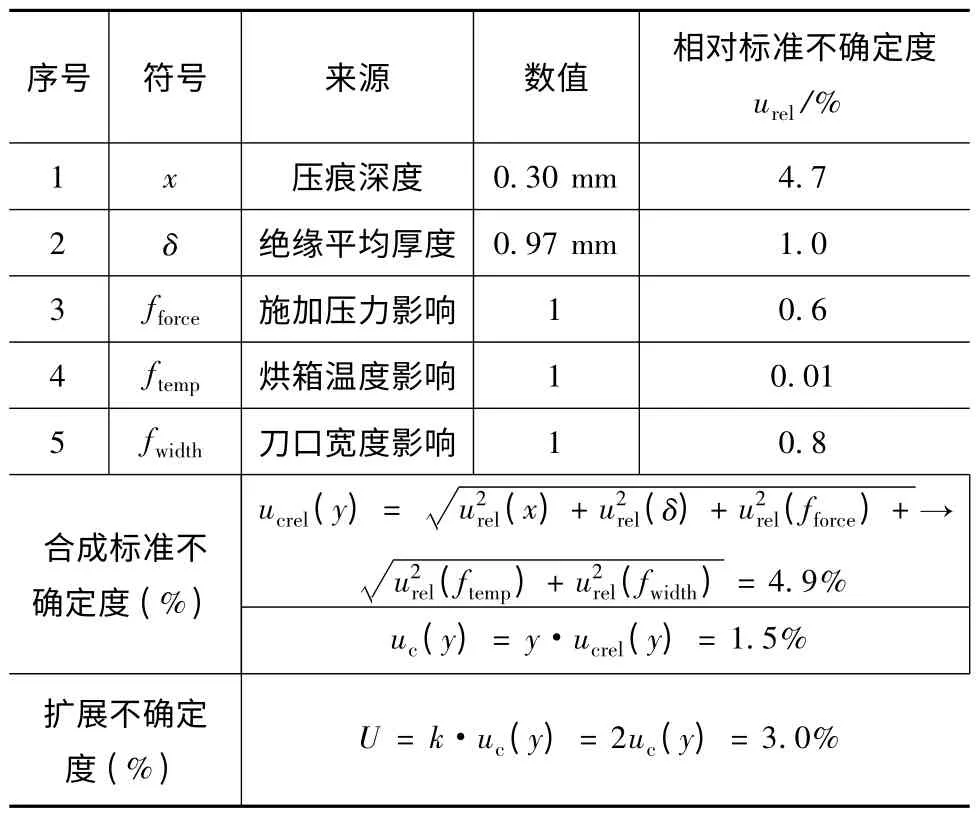
表3 测量不确定度分量汇总表

5 合成标准不确定度ucrel(y)

用式(4)将以上所列的不确定度分量进行合成得:

6 测试结果

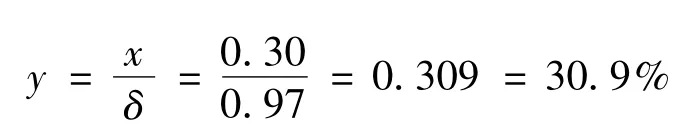
于是合成标准不确定度uc(y)为:

7 扩展标准不确定度

取包含因子k=2，于是扩展不确定度为:

8 测量不确定度报告

被测样品电缆的PVC绝缘层高温压力试验结果为30.9%。其扩展不确定度为U=3.0%，它是由合成标准不确定度1.5%和包含因子k=2的乘积得到的，对应置信概率约为95%。

9 结束语

本文结合数据统计与经验估计，重点分析可能对测量结果造成主要影响的不确定度分量并进行计算，由计算结果可以看出压痕深度是贡献最大的分量。

在建立的数学模型时考虑到，虽然绝缘高温压力试验的最终测试结果有标准规定的表达式，但施加压力、烘箱温度和刀口尺寸在实际试验中都是重要的影响量，不能被省略。本文采用黑箱模型方式把这些影响因素用修正因子的形式写入数学模型的输入量中，因为这些修正因子的数学期望都等于1，因此对计算结果没有影响，只需通过B类评定得到它们的相对不确定度。

观察数学模型可以发现，该模型仅包含了各输入量的乘积形式，故选用相对不确定度要比直接用绝对不确定度计算更为简便。

［1］GB/T 2951.31—2008电缆和光缆绝缘和护套材料通用试验方法 第31部分:聚氯乙烯混合料专用试验方法——高温压力试验——抗开裂试验［S］.

［2］JJF 1059.1—2012测量不确定度评定与表示［S］.

［3］CNAS－GL10:2006材料理化检验测量不确定度评估指南及实例［S］.

［4］倪育才.实用测量不确定度评定(第3版)［M］.北京:中国计量出版社，2009.202-213.

［5］孔祥华.材料物理基础(第1版)［M］.北京:冶金工业出版社，2010.247-260.

［6］季 红.电线电缆绝缘高温压力试验研究［J］.电线电缆，2012(4):32-34.

［7］谢云涛，陈 敏.电线电缆管状试件抗张强度检测不确定度的评定与分析［J］.电线电缆，2014(4):34-36.

［8］热膨胀系数表［EB/OL］.维基百科.http://zh.wikipedia.org/wiki/热膨胀系数.