大数据环境下的动态最短路径算法*

徐建闽　王钰　林培群

(华南理工大学 土木与交通学院， 广东 广州 510640)



大数据环境下的动态最短路径算法*

徐建闽王钰林培群

(华南理工大学 土木与交通学院， 广东 广州 510640)

摘要：数量庞大、类型复杂的海量数据给智能交通带来了新的挑战.文中对交通诱导中的动态最短路径问题进行了研究,提出了动态交通网络数学模型,在此基础上设计了考虑交叉口延时的动态最短路径算法,并使用当前流行的大数据技术,设计了基于HaLoop MapReduce的动态最短路径并行计算模型,最后在连续流智能交通管控平台上对算法进行了测试.实验结果表明，文中设计的算法和基于大数据的并行计算模型可以有效地查找到大规模路网中的动态最短路径,同时能很好地满足实时性需求.

关键词：大数据;动态最短路径算法;交叉口延误;路径诱导

交通诱导系统(TRGS)是智能交通系统(ITS)研究的一个重要方面,也是改善城市交通状况的最佳途径之一.随着智能交通系统、IT技术以及网络与通信技术的发展,动态路径诱导系统(DRGS)逐渐成为人们关注的热点.DRGS基于道路的实时交通状态,为出行者提供最少出行时间的路径.

由于路段和交叉口的交通阻抗随时间不断变化,因此城市交通网络是动态网络或时间依赖网络(TDN).同时,交叉口延时以及交通状态的随机性造成了城市路网的非先进先出(FIFO)性.如何在这些复杂限制条件下高效求解最优路径,是动态路径诱导问题研究的核心.目前,国内外对动态最短路径(DSP)问题的研究主要集中在如何对动态信息进行处理与如何提高算法的实时性这两个关键性问题上.

由于数据资源和计算效率的限制,目前的TRGS无法做到准确、及时的动态诱导.但随着智能移动设备的大量应用以及城市道路基础设施的不断完善,这些设备和设施产生了海量异构的实时数据,为实时的动态路径诱导提供了数据基础.然而,由于求解动态最短路径的模型复杂,针对海量数据的实时计算与分析在传统数据技术架构下很难实现.

大数据技术是新的海量数据处理技术,在很多领域都取得了显著的应用效果,但在智能交通领域的应用还刚刚起步.然而大数据技术使得及时获取城市路网中实时的路段行程时间与交叉口延误时间成为可能,也为大规模路网环境下的动态最短路径的计算提供高性能的分析与处理能力.文中拟在大数据环境下建立一套完整的理论和算法,以解决城市交通的动态最短路径求解问题.

1相关研究

目前基本的最短路径(SP)问题已有大量成熟的算法,如标号设定法、标号修改法、动态规划法、启发式和双向启发式算法、基于流体神经网络的算法等[1- 4].然而,由于路网交通的复杂性以及交通流状态的动态性,基本的SP算法无法有效解决交通系统中的路径诱导问题.

在基本SP算法的基础上,很多学者对DSP问题展开了研究.Hall[5]首次研究了交通网中路段通行时间是随机并且依赖于时间情况下的最短路径问题.Ziliaskopulos等[6]提出了动态最短路径问题.

针对动态网络的建模,Chabini等[7- 8]提出将时间离散化处理,即将时间区域划分为一系列时间片段,假定路段行驶时间在一个时间片段内保持稳定,这样动态网络可以建模为静态模型.针对动态网络最短路径的搜索算法,当网络的权值都服从FIFO原则的一致性假设时,可以用扩展的静态SP算法(如Dijkstra算法等)来求解[9].当网络的权值不满足FIFO条件时,静态SP算法都不再适用.Pallottino等[10]提出了一个适用于非FIFO条件的DSP算法范例——Chrono-SPT,给出了无环图的最小代价路径问题的一般解法,并对其理论上的时间复杂度进行了初步分析.Orda和Rom[11]给出了在节点允许等待的非FIFO网络中,节点最优等待时间和最优路径的计算方法.由于城市道路的交叉口处不允许随个人意愿等待,因此这种方法不能用于城市路网的动态最短路径计算.谭国真等[12]研究了没有任何限制性条件下的动态网络模型,并提出了适用于非FIFO网络的SPTDN算法.SPTDN算法提供了一般性的计算方法,其计算效率不是最优的,而且该算法是从后往前计算的,所以限制了某些应用.

为了解决包含有交叉口延误和转向限制的SP问题,国内外学者提出了多种方法.扩展网络法[13]与对偶网络法[14]将原网络进行一定转换,然后采用基本的SP算法求解.文献[15]中提出了一个基于弧标号的标号修正算法.但是目前对于动态网络的交叉口延误和转向限制的研究还很少.

随着人工智能研究的发展,一些新的智能算法不断被应用在最短路径的求解中,主要包括遗传算法[16]、神经网络算法[17]、蚁群算法[18]、人工免疫算法[19]、人工鱼群算法[20]、粒子群算法[21]等.杨庆芳等[22]提出用基于MapReduce的并行遗传算法解决静态最短路径问题.Wen等[23]提出用遗传算法来求解动态最短路径.由于智能算法本身比较复杂、计算量大,因此以上算法都存在搜索时间长或者计算精度低的问题.

综上所述,目前大多数DSP算法的前提是FIFO网络,且没有考虑交叉口延误与转向限制,这与实际的交通网络不相符.同时,DSP的计算对系统在大负荷情况下的实时性要求非常高,这也是实现动态路径诱导面临的瓶颈问题.

2动态交通网络模型

2.1　动态交通网络数学模型

根据利用多种交通感知技术所获取的海量交通数据,文中建立了更加精确的动态交通网络数学模型.动态路径问题是非马尔可夫(Markov)性的,因此动态网络的建模方法与静态网络不同.此外,在城市路网中,由于交叉口转向而引起的时间延迟可以达到全部行程时间的17%～35%[24],交叉口延误已经成为DSP问题的一个重要影响因素.文中给出的动态交通网络模型满足非马尔可夫性质,同时描述了交叉口不同流向的实时转向延误,对城市交通流的运行进行了精确的刻画,展现了城市路网交通的实时性和随机性.

将动态交通网络映射成一个连通的动态带权有向图，G=(V，A，W，D).V={v1,v2，…,vn},为有限节点集,表示交通网络上所有节点,由道路的交叉口或者道路的起点/终点抽象而成.A⊆V={ai,j|i≠j,vi,vj∈V},为有限弧集,表示网络上所有有向边,由道路线路抽象而成.W={wi,j(t)|ai,j∈A,t∈T},为弧权集合,表示动态路段行程时间.wi,j(t)表示t时刻从交叉口vi出发到达交叉口vj的行程时间.T=[t0,tu],是诱导时间范围的闭区间.D={di,j,k(t)|(ai,j,aj,k∈A,t∈T)},为节点权集合,表示动态交叉口延误时间.di,j,k(t)表示t时刻在交叉口vj处,由交叉口vi方向转向交叉口vk方向的延迟时间.

对动态网络的建模,文中采用将时间离散化处理的方式,把诱导的时间区域划分为一系列较小的时间片段.时间区间T可以表示为T={t0,t0+Δ,t0+2Δ,…,t0+(q-1)Δ},Δ是时间间隔,q为时间片段数.为了保证计算的精确性,取1 min作为一个时间片段,即各节点(源节点和目的节点除外)出发时间的间隔为1 min.根据交通网络的特点,假定路段的行程时间与交叉口延时分别在5 min与1 min内保持稳定.

假如静态网络R的节点数为n,边数为m,那么扩展为时间片段数为q的动态网络G以后,网络的规模和复杂性都发生了变化.其中,V×T={(vi,th)|vi∈V,th∈T}，表示节点的状态空间,有序对(vi,th)表示在th时刻的交叉口vi.A×T={(ai,j，th)|ai,j∈A，th∈T},表示弧的状态空间,有序对(ai,j,th)表示在th时刻的路段ai,j.与静态网络相比,动态网络的规模扩大了,同时复杂性提高了.

2.2　动态交通网络优化模型

动态交通网络的最短路径是指在t时刻从源节点出发到达目的节点的所有路径中走行时间最少的路径.

定义在动态网络中,设fi(t0)表示在t0(t0∈T)时刻从源节点v0出发到达节点vi的时间，pi(t)表示交叉口vi在t时刻的前置交叉口，dpi,i,j(t)表示t时刻在交叉口vi处由交叉口vi的前置交叉口pi(t)方向转向交叉口vj方向的延迟时间.

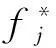
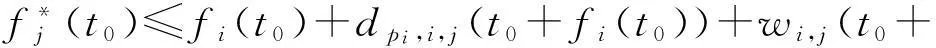
fi(t0)+dpi,i,j(t0+fi(t0))).

车辆在t0+fi(t0)时刻到达交叉口vi,dpi,i,j(t0+fi(t0))表示从交叉口vi转向交叉口vj方向所产生的时间延迟；wi,j(t0+fi(t0)+dpi,i,j(t0+fi(t0)))表示车辆经历了转向延迟后,由交叉口vi到交叉口vj的行程时间.

3考虑交叉口延误的动态最短路径算法

通过对海量交通数据的精确提炼,利用大数据技术高效的处理能力,设计了改进的DSP算法.算法按照时间顺序从源节点开始依次处理各交叉口节点直到目的节点.每一个交叉口节点(源节点除外)都对应一到多个到达时间.从出发时间开始以1 min作为一个时间间隔,记录每个时间节点所对应的交叉口节点.采用桶列表[10]B(B={B1,B2,…,Bn})来存放在不同时间节点将要被访问的交叉口节点.Bh表示在th时刻将要被访问的节点集合.如果出发时间为tθ,则Bθ={v0}为第一个桶,它只包含了源节点v0.处理过的节点被标记为(节点,时间,前置节点)组合,“时间”为达到该节点的时刻,“前置节点”为对应该时刻的前置节点.从桶中删除被处理过的节点,当所有桶为空时,算法结束.

算法步骤如下.其中,FS(vi)表示节点vi的紧后节点的集合,pj(th)表示节点vj在th时刻的紧前节点,vi(th)表示在th时刻的vi节点.Bh存储th时刻将要选择的节点.设源节点为v0,目的节点为vn,出发时间为tθ.

步骤1(初始化)

Bθ:={v0};

Bc:=∅(∀c≠θ);

h:=θ;

步骤2

SelectviFromBh

Bh:=Bh{vi};

Ifvi≠vn

For 每一个vj∈FS(vi)进行如下操作:

ts=th+dpi,i,j(th)+wi,j(th+dpi,i,j(th));

pj(ts)=vi(th);

Ifvj∉BsThenBs:=Bs∪vj;

End For

End If

End Select

IfBh≠∅ Then goto 步骤2;

步骤3

h=h+1;

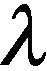
goto 步骤2;

Else

算法结束.

文中提出的DSP算法既适合于FIFO网络,也适合于非FIFO网络,并兼顾了交叉口的延误和转向限制.在实时性方面,算法利用桶结构提高了计算效率,同时便于在大数据处理平台上进行并行化处理.从前往后的计算方式有利于在求解过程中及时应用最新的交通状态数据.

4基于Hadoop MapReduce的算法实现

实现动态路径导航的瓶颈之一是算法对海量数据的处理能力.文中引进大数据技术中的MapReduce计算模型,对诱导算法进行并行化处理.Map-Reduce技术是一种简洁的并行计算模型,用于大规模数据集的处理和分析,具有较高的处理速度和可靠性,在大数据计算领域得到了广泛应用.

MapReduce把一个作业的执行过程分为Map和Reduce两个阶段.在Map阶段,由Map函数对输入的数据进行处理,然后将结果写到本地磁盘上;在Reduce阶段,由Reduce函数处理Map阶段的输出,并将最终结果写到分布式文件系统(HDFS)上.

目前流行的Hadoop MapReduce框架在处理迭代式流程时存在不足,表现在:每次迭代都需要重复创建所有作业(Job),并进行磁盘读写和数据传输,使得每次迭代的代价非常高.因此Hadoop MapReduce不能很好地支持迭代式作业.由于文中的DSP算法是迭代式计算,所以文中采用了对传统Hadoop MapReduce进行改进后的HaLoop[25]框架.HaLoop设计了新的作业结构,使一个作业包含多个Map-Reduce任务对.此外,HaLoop将静态变量缓存到各个任务服务器(TaskTracker),每次迭代重用这些数据,大大减少了输入输出.HaLoop能高效地支持迭代和递归分析.

文中采用网络分割的方法实现并行计算.首先使用Metis算法将路网进行划分,把网络分割成P个子网，每个子网由1个HaLoop的工作(Worker)节点机器负责.每个工作节点机器平均划分n=N/P个网络节点,其中N表示总节点数.工作节点机器的计算任务是计算从出发时间开始,在某个时间段内每1 min从路径在所管辖子网的开始节点出发,到达中间各节点以及子网边界节点的时间,并记录每个节点的到达时刻和相应的前置节点.HaLoop的主(Master)节点机器最终将各个子网的计算结果进行汇总,从目的节点的最早到达时间开始反推,得到整个网络的动态最短路径.根据历史数据,可以得到每对OD(出发地,目的地)最长的行程时间,将这个时间作为各个节点机器计算的时间范围.例如:在9:00从节点v0出发到节点vn,历史数据中最长的行程时间为120 min,那么每个工作节点机器承担的计算任务是计算车辆在从9:00到11:00出发(每分钟作为一个出发时间点),沿着子网内路径依次到达各节点的时间.此时,除源节点v0和目的节点vn外,路径的其余节点都对应120个出发时间.

(1)数据输入

输入数据分为两种类型:一种是路段数据;另一种是交叉口数据.输入文件中的每一行为1个路段或者交叉口在24 h内的实时交通数据.

路段数据结构和交叉口数据结构如图1所示.

路段ID(始节点ID,终节点ID)以5min为间隔的行程时间序列相邻交叉口序列

(a)路段数据结构

(b)交叉口数据结构

图1路段数据结构和交叉口数据结构

Fig.1Date structure of road section and crossing

对于路段数据,“键”为路段ID;“值”包括:(路段始节点ID,路段终节点ID),24 h内以5 min为间隔的路段行程时间序列,相邻交叉口ID序列.对于交叉口数据,“键”为(交叉口ID,上游交叉口ID,转向交叉口ID);“值”为24 h内以1 min为间隔的转向延迟时间序列.HaLoop将数据进行切分后,根据节点所在的不同子网,分发到多个Map任务.

(2)Map阶段

Map函数将所对应子网的路段行程时间和交叉口延时数据以及计算时间范围作为输入,按照广度优先的原则对图的结构按照层次进行遍历.Map函数根据各时间段的行程时间和交叉口延误数据,计算到达下一交叉口的时间,最后产生键/值形式的中间值.中间值的“键”为到达交叉口的时间,“值”分别为交叉口ID、前驱交叉口ID、到达前驱交叉口的时间.

Map阶段的输出格式如图2所示.

到达交叉口的时间交叉口ID前驱交叉口ID到达前驱交叉口的时间

图2Map阶段的输出格式

Fig.2Output format of Map stage

(3)Reduce阶段

HaLoop将所有具有相同“键”的“值”集合在一起传递给Reduce函数.Reduce函数对具有相同到达时间的交叉口的“值”集合进行处理,产生新的桶.Reduce阶段的输出格式如图3所示.

到达交叉口时间(交叉口ID,前驱交叉口ID,到达前驱交叉口时间)序列

图3Reduce阶段的输出格式

Fig.3Output format of Reduce stage

(4)HaLoop MapReduce的迭代

每次Reduce阶段的输出又作为下一轮Map阶段的输入,作业服务器(JobTracker)的循环控制模块不断启动Map-Reduce计算,通过多次迭代完成路径所包含的所有交叉口的计算.在迭代过程中,HaLoop的主节点机器负责Job内的循环控制,直到迭代计算结束.迭代过程如图4所示.

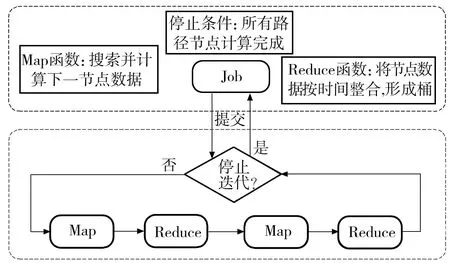
图4基于HaLoop MapReduce的动态最短路径算法迭代过程图

Fig.4Iterative process of dynamic shortest path algorithm based on HaLoop MapReduce

文中DSP算法中，在最坏的情况下，第1阶段,工作节点机器计算的时间复杂度为O(Mq/P),其中M为交通网络的弧段数,时间区间T为根据历史数据确定的所对应OD的最长行程时间.第2阶段,主节点机器汇总计算的时间复杂度为O(N).由于O(Mq/P)>O(N),因此假设不考虑通信成本，则文中DSP算法的时间复杂度为O(Mq/P).

每个工作节点机器负责1个子网的计算,并把子网的最终计算结果一次性提交到主节点机器.子网中所有相关节点处理完成之前,各工作节点机器之间并无通信成本产生.此外,主节点机器和工作节点机器之间的通信成本也远小于计算时间复杂度.

通过基于HaLoop MapReduce框架的并行化处理,文中DSP算法的执行性能大幅提升.该算法可以在可伸缩的大规模集群上并行执行,并可以处理大规模的交通数据,实现在大数据环境下的动态路径诱导.

5实验与结果分析

文中设计研发了连续流智能交通管控平台,并在此平台上对文中算法进行了测试.连续流智能交通管控平台分析处理多源交通数据,实现智能高效的交通管理与控制、交通决策支持以及警用资源管理等功能.测试系统部署在HaLoop集群,每个节点机器采用相同的软件配置:操作系统采用Linux CentOS 7.1,软件环境采用HaLoop+Java SE 6+SSH(struts2.3.16,spring3.2.8,hibernate3.6.10).路网和交通数据文件存储在ORACLE数据库中,使用ORACLE的大数据连接器(Big Data Connectors)将相关的数据写入到HDFS中.

算法采用Java语言实现,在基于广州市电子地图的动态网络上进行了测试.广州市区道路交通网络包含有21 326个节点,42 632个路段,属于大型路网.各路段行程时间和交叉口延误数据根据21周的历史数据统计值确定.出发时间以及交叉口延时以1 min为一个时间间隔;路段的行程时间以5 min为一个时间间隔.文中使用网络分割工具Metis把路网分成了10个区域.将路网图及其分割图部署到了11台PC计算机上,形成了小型集群环境.每台机器拥有主频为3.3 GHz的4核处理器、4 G内存和800 GB可用硬盘空间.其中一台机器为主节点机器,作为HDFS的管理者(NameNode)和MapReduce的作业服务器,其余机器为工作节点机器,作为工作者(DataNode)和任务服务器.

在路网中选择了12个OD对文中算法进行测试,测试结果如表1所示.

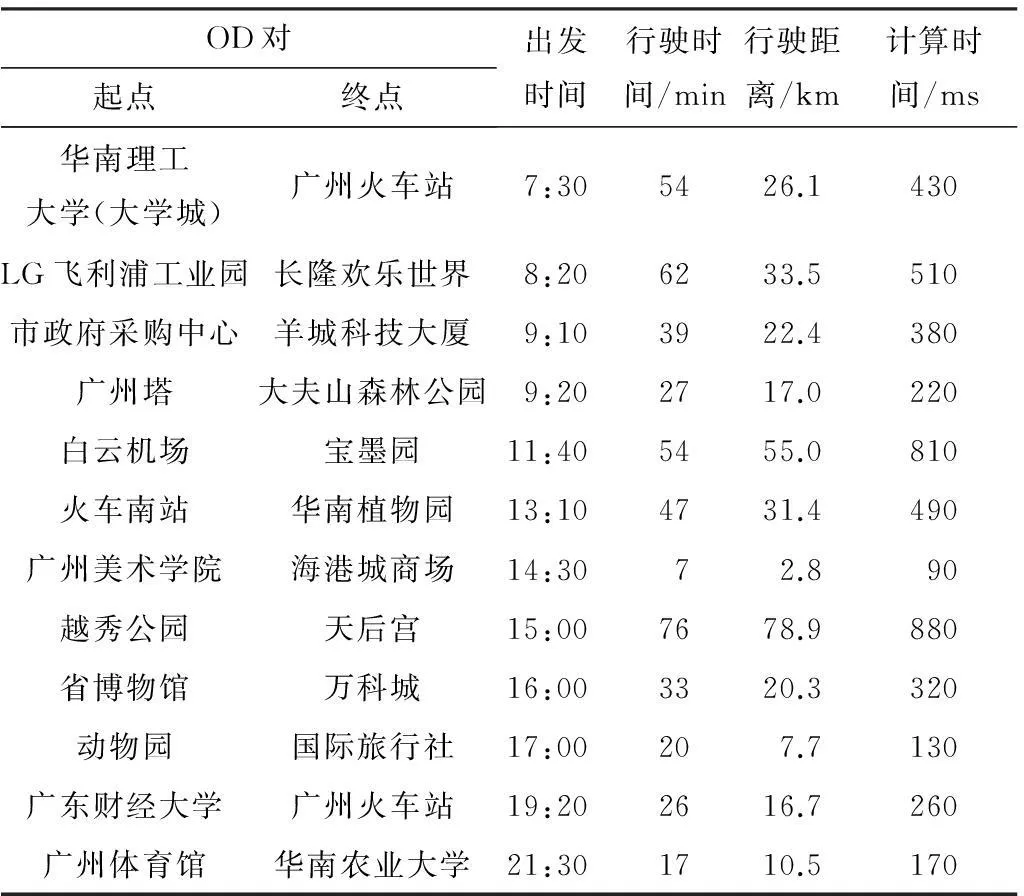
表1　12个OD对动态最短路径的测试结果

测试结果表明:对于长度为50 km左右的长路径,计算时间在1 000 ms以内;长度为30 km左右的中等长度路径,计算时间在700 ms以内;长度为10 km左右的短途路径,计算时间为300 ms以内.文献[22]中,求解静态最短路径的最高性能的运行时间是7.8 s;文献[23]中,对动态最短路径的平均计算时间是7.18 s.文中的实验结果与之相比,计算效率有较大提升,可以满足大规模路网中动态路径诱导的需求.

6结语

文中对大数据环境下动态最短路径问题进行了研究,利用大数据的高性能分析与处理技术建立了动态交通网络数学模型,在此基础上提出了一种改进的基于离散时间的动态最短路径算法.该算法具有适用于动态非FIFO网络和兼顾交叉口延时两种特点,真实地反映了城市交通运行的特征,更加适合于大数据环境下的动态路径诱导.在算法的实现上,文中采用了当前流行的大数据技术,利用HaLoop MapReduce框架,实现了对交通数据的分布式并行处理,大大提高了路径的求解效率.最后,在连续流智能交通管控平台的分布式集群环境中对算法进行了测试.测试结果表明,动态最短路径算法以及基于HaLoop MapReduce的并行模式在解决大规模网络的动态最短路径问题上是非常有效的,比传统动态最短路径算法具有更高的精确性与实时性.未来对动态最短路径问题的研究将进一步探讨如何利用大量的异构实时交通数据,对路段的行程时间进行较为准确的预测,使路径诱导的准确性进一步提升.

参考文献：

[1]Ahuja R K,Magnanti T L,Orlin J B.Network flows:theory,algorithms and applications [M].Englewood Cliffs,NJ:Prentice-Hall,1993.

[2]Topkins Donald M.Akshortest path algorithm for adaptive routing in communications networks [J].IEEE Trans Communications,1988,36(7):855- 859.

[3]Shi Hanmao.Time work tradeoffs of the single source shortest paths problem [J].Journal of Algorithms,1999,30(1):19- 32.

[4]Frigioni Daniele.Fully dynamic algorithms for maintaining shortest paths trees [J].Journal of Algorithms,2000,34(2):351- 381.

[5]Hall R W.The fastest path through a network with random time-dependent travel times [J].Transportation Science,1986,20(3):182- 188.

[6]Ziliaskopulos A,Mahmassani H.Time-dependent shortest path algorithms for real-time intelligent vehicle highway system applications [J].Transportation Research Records,1993,1408:94- 100.

[7]Chabini Ismail.Discrete dynamic shortest path problems in transportation applications:complexity and algorithms with optimal run time [J].Transportation Research Records,1998,1645:170- 175.

[8]Kim Seongmoon,Lewis Mark E,White Chelsea C.Optimal vehicle routing with real-time traffic information [J].IEEE Transportation on Intelligent Transportation Systems,2005,6(2):178- 188.

[9]Kaufman D E,Smith R L.Fastest path in time-dependent networks for intelligent vehicle-highway systems application [J].Intelligent Vehicle-Highway Systems Journal,1993,11(1):1- 11.

[10]Pallottino S,Scutella M G.Shortest path algorithms in transportation models:classical and innovative aspects[C]∥Marcotte P,Nguyen S.Equilibrium and Advanced Transportation Modeling.Boston:Kluwer,1998:245- 281.

[11]Orda Ariel,Rom Raphael.Distributed shortest-path protocols for time-dependent networks [J].Distributed Computing,1996,10(1):49- 62.

[12]谭国真,高文.时间依赖的网络中最小时间路径算法 [J].计算机学报,2002,25(2):165- 171.

Tan Guo-zhen,Gao Wen.Shortest path algorithm in time-dependent networks [J].Chinese Journal of Computers,2002,25(2):165- 171.

[13]Yagar S.Dynamic traffic assignment by individual path minimization and queuing [J].Transportation Research,1971(5):179- 196.

[14]Anez J,Barra T,Perezl B.Dual graph representation of transport networks [J].Transportation Research B,1996,30(3):209- 216.

[15]高明霞,贺国光.考虑交叉口延误和转向限制的弧标号最短路径算法 [J].兰州交通大学学报,2011,30(6):111- 114.

Gao Ming-xia,He Guo-guang.An arc labeling algorithm for shortest path problem considering turn penalties and prohibitions at intersections [J].Jourrml of Lanzhou Jiaotong University,2011,30(6):111- 114.

[16]胡小兵,黄席樾.对一类带聚类特征TSP问题的并行遗传算法求解 [J].计算机工程与应用,2004,40(35):66- 74.

Hu Xiao-bing,Huang Xi-yue.Solving traveling salesman problem with characteristic of clustering by parallel genetic algorithm [J].Computer Engineering and Applications,2004,40(35):66- 74.

[17]Hopfield J J,Tank D W.Neural computation of decisions in optimization problems [J].Biological Cybernetics,1985(3):141- 152.

[18]黄贵玲,高西全,靳松杰,等.基于蚁群算法的最短路径问题的研究和应用 [J].计算机工程与应用,2007,43(13):233- 235.

Huang Gui-ling,Gao Xi-quan,Jin Song-jie,et al.Study and application on shortest path search problem based on ant algorithm [J].Computer Engineering and Applications,2007,43(13):233- 235.

[19]林洁,杨立才,吴晓晴,等.求解动态路径诱导K路最短问题的人工免疫优化方法 [J].山东大学学报:工学版,2007,37(2):103- 108.

Lin Jie,Yang Li-cai,Wu Xiao-qing,et al.Artificial immune optimization method for solving theK-shortest paths search in dynamic route guidance systems [J].Journal of Shandong University:Engineering Science,2007,37(2):103- 108.

[20]马宪民,刘妮.自适应视野的人工鱼群算法求解最短路径问题 [J].通信学报,2014,35(1):1- 6.

Ma Xian-min,Liu Ni.Improved artificial fish-swarm algorithm based on adaptive vision for solving the shortest path problem [J].Journal on Communications,2014,35(1):1- 6.

[21]魏明,靳文舟.求解车辆路径问题的离散粒子群算法 [J].计算机科学,2010,37(4):187- 191.

Wei Ming,Jin Wen-zhou.Discrete particle swarm optimization algorithm for vehicle routing problems [J].Computer Science,2010,37(4):187- 191.

[22]杨庆芳,梅朵,郑黎黎,等.基于云计算的城市路网最短路径遗传算法求解 [J].华南理工大学学报:自然科学版,2014,42(3):166- 169.

Yang Qing-fang,Mei Duo,Zheng Li-li,et al.Cloud computing-based genetic algorithm to solve the shortest path in urban road networks [J].Journal of South China University of Technology:Natural Science Edition,2014,42(3):166- 169.

[23]Wen Hui-ying,Xu Jian-min,Zou Liang.Genetic algorithm-based computation of the shortest path in discrete-time dynamic networks [J].Journal of South China University of Technology:Natural Science Edition,2008,36(2):13- 28.

温惠英,徐建闽,邹亮.基于遗传算法的离散时间动态网络最短路径求解 [J].华南理工大学学报:自然科学版,2008,36(2):13- 28.

[24]Caldwel T.On finding minimum routes in a network with turn penalties [J].Communication of the ACM,1961,4(2):107- 108.

[25]Bu Yingyi,Howe Bill,Balazinska Magdalena,et al.HaLoop:eficient iterative data processing on large clusters [J].Proceedings of the VLDB Endowment,2010,3(1/2):285- 296.

Foundation item: Supported by the National Natural Science Foundation of China(51078150)

A Dynamic Shortest Path Algorithm for Big Data

XuJian-minWangYuLinPei-qun

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong, China)

Abstract:Massive heterogeneous data processing has been a great challenge to intelligent traffic applications.In this paper, the dynamic shortest path problem in traffic guidance is dealt with, and a mathematic model of dynamic traffic networks is constructed. Then, a dynamic shortest path algorithm considering the intersection delay is proposed. Furthermore, a distributed and parallel processing model for solving the dynamic shortest path problem is presented based on HaLoop MapReduce and by using big data techniques. Finally, the proposed algorithm is tested on the intelligent traffic management and control platform based on continual flow. Experimental results demonstrate that the proposed algorithm and the presented model can effectively find the dynamic shortest path in large scale networks and can meet the real-time requirement.

Key words:big data; dynamic shortest path algorithm; intersection delay; route guidance

文章编号：1000- 565X(2015)10- 0008- 08

作者简介：王强(1973-)，男，博士后，广东华路交通科技有限公司高级工程师，主要从事路桥检测评估研究.E-mail： wq2351@163.com

基金项目：*国家自然科学基金资助项目(51078150)；交通运输部建设科技项目(2011318223390)；广东省交通运输厅科技项目(科技-2009- 01- 001- 05)

收稿日期：2015- 01- 07

中图分类号：U491.2

doi:10.3969/j.issn.1000-565X.2015.10.001