考虑列车容量限制的地铁网络客流分配模型*
2015-02-18周玮腾韩宝明
周玮腾 韩宝明,2†
(1.北京交通大学 交通运输学院,北京 100044; 2.北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044)
考虑列车容量限制的地铁网络客流分配模型*
周玮腾1韩宝明1,2†
(1.北京交通大学 交通运输学院,北京 100044; 2.北京交通大学 轨道交通控制与安全国家重点实验室, 北京 100044)
摘要:城市地铁网络客流分配对于城市轨道交通网络化运营管理具有重要意义.既有研究较少地考虑基于时刻表条件下的列车容量限制对于客流分配的影响.文中通过构建时刻表扩展网络,设计时刻表扩展网络下的k短路径搜索算法,考虑列车容量限制下乘客的拥挤因素和留乘延误因素,构建随机用户均衡条件下的客流动态分配模型,并设计了求解算法.通过北京地铁网络客流分配实例进行模型验证,并分析了参数的敏感性.实例证明,模型具有较高的计算精度(相对误差9.5%~11.2%)和收敛速度,能满足地铁大规模网络客流分布的分析和评估需求.
关键词:地铁;客流分配;时刻表;列车容量;留乘
我国已经逐渐进入了城市轨道交通网络化运营时代.随着地铁线网规模的逐渐增大,线网复杂度增高,乘客出行的可替代路径越来越多,影响乘客路径选择的因素逐渐增多,有效推算乘客路径选择概率,进而科学有效计算客流的实时动态分布状态,实现线网客流在不同运营线路间的评估和分析,对于网络化运营管理具有重要的现实意义.
目前,我国城市地铁运营管理部门建立了自动售检票系统(AFC)进行客票数据管理,根据AFC系统采集的乘客出行记录,可以获得乘客的进出站点和时间,因此可以推算网络化运营条件下受到多种因素(如车站周围土地利用状况、路网完善程度等)影响的乘客出行的OD分布不确定因素,进而获取实时的OD分布信息,为客流分配提供明确的OD输入信息.然而,我国地铁运营系统多采用“一票制”运营模式,在该换乘条件下的乘客出行的中间信息(如换乘和路径选择等)难以通过AFC系统采集的乘客出行客票记录进行推算.在这种情况下,地铁线网客流在路网上的实时分布状态问题实质上是一个具备明确OD信息输入的黑箱问题.客流实时动态分布推算一直是国内外学者研究的重点,针对该问题主要集中在于线网客流分配模型构建和客流分配算法等方面,并分别形成了用户均衡分配模型和效用概率分配模型,辅之形成了静态配流方法和动态配流方法.国内的研究[1-2]主要以均衡配流模型为主,一般采用静态配流算法进行模型的求解.由于模型应用对于算法效率有极高要求,因此研究[3]提出了利用效用概率分配方法,并应用于北京地铁的客运管理生产实践中.相比于国内理论研究方法,国外的研究则多应用于常规公交客流分配,分别形成了基于发车频率和基于时刻表的应用于公交客流分配的模型[4-6].考虑到客流分配的动态性,文献[7]中通过建立基于时刻表的动态均衡分配模型,建立包括出行时间、候车时间和换乘惩罚因素的广义费用函数,通过模拟乘客登乘排队情况,设计改进相继平均法(MSA)结合仿真算法进行模型求解.文献[8]中在前人的研究基础上,形成基于时刻表的运输系统模型和动态分配方法论.在对于列车容量因素的考虑下,多数学者对列车容量约束的动态均衡模型展开研究.文献[9]中提出了基于发车频率的客流分配模型,模型考虑乘客在乘车过程中是否能寻找到座位的概率,并提出了求解算法.文献[10]中提出了基于时刻表的历时网络双层模型和考虑公交容量的客流动态加载方法,并集中论述了文献[11]中阐述的连续日和日内两种情况下的分配模型;文献[12]中考虑了结合公交时刻表,以乘客出行策略最优为目的,建立了针对公交网络的动态用户平衡模型.
但是,由于既有的研究大部分集中在公共交通的客流分配上,很少文献专门针对城市地铁交通网络进行动态客流分配的研究.作为路权独立的交通方式,地铁系统相比于地面公交系统受到其他交通方式干扰较少,能更好地按照列车时刻表严格执行运输计划.因此应构建基于时刻表的网络客流分配模型描述和反映客流在每趟列车的分布状态,进而推算客流线网分布状态.同时,乘客在线网上的动态分布过程是乘客与运载列车、乘客与乘客之间的动态交互过程,分布随时间动态变化且乘客运载受列车容量限制,客流动态分配的过程中应严格考虑列车的承载能力.
文中基于已有研究,考虑城市地铁交通的结构特性和乘客的行为特征,提出了针对城市地铁交通的基于时刻表的客流分配模型和算法.首先,结合实际的列车时刻表和实际的线网拓扑结构,构建城市地铁交通时刻表扩展网络模型;构建时间扩展网络下的时变k短路径搜索算法,进行路径搜索并设定相应规则筛选有效出行路径,构成时间扩展网络下的有效k短路径集,将乘客出行的物理网络路径转化为时刻表规则下的列车运行路径;然后基于乘客出行行为影响因素,提出基于乘客出行策略与列车容量限制的路径广义费用函数,构建基于时刻表扩展网络的城市地铁交通网络随机均衡分配模型,采用MSA算法结合乘客行为仿真模拟方法进行模型求解;最后结合AFC采集的乘客出行数据,通过实际的北京地铁网络数据构建算例进行模型的验证与分析.
1城市地铁交通时刻表扩展网络
城市地铁交通网络是由轨道交通静态拓扑网络和轨道列车动态运行网络构成的复合嵌套网络.构建城市地铁交通时刻表扩展网络的基础是根据列车时刻表列车的到发时间,将拓扑网络的空间线路和节点进行时间维的关联和扩展.通过列车的运行径路及其到发时间将静态网络的节点进行关联,形成按照列车车次扩展的运行图扩展网络.将城市地铁交通网络G(N,A,L)进行时刻表扩展的具体过程如下:
步骤1按照时刻表上所有线路每个车次经停的物理车站节点进行时间维扩展,即为物理节点增加列车的到站和离站时间标签,通过不同列车的时间标签扩展物理节点,同时通过扩展物理节点表示列车的到站和离站站点;
步骤2列车通过时刻表时间通过到发将不同扩展节点进行连接,形成的弧序列为列车运行径路,通过列车运行径路,将同一线路相同车次的列车连接相邻车站节点的离站时间和到站时间,形成区间运行弧;
步骤3将同一物理车站的不同线路列车的到站和离站时间节点通过换乘弧连接.
利用图G(N,A,LN,T)表示扩展后的网络架构,其中N表示扩展车站节点集合,A表示弧集合,LN表示属于线路L的车次集合,T表示列车在车站节点到达和出发时间集合.网络中基本的元素表示如下.
(1)时变扩展节点

(2)时变扩展弧

(1)
(2)
(3)
(3)时变扩展路径
在时刻表扩展网络中,任意一对OD站点之间的时变扩展弧在一个时间段内的连接序列叫做OD间的时变扩展路径,其必须满足线路节点之间的连通关系,同时得满足列车的可行条件.设城市地铁交通局部网络如图1所示,则车站a1至b3在早7:30~8:00之间的动态时变扩展路径的扩展弧如图1所示.
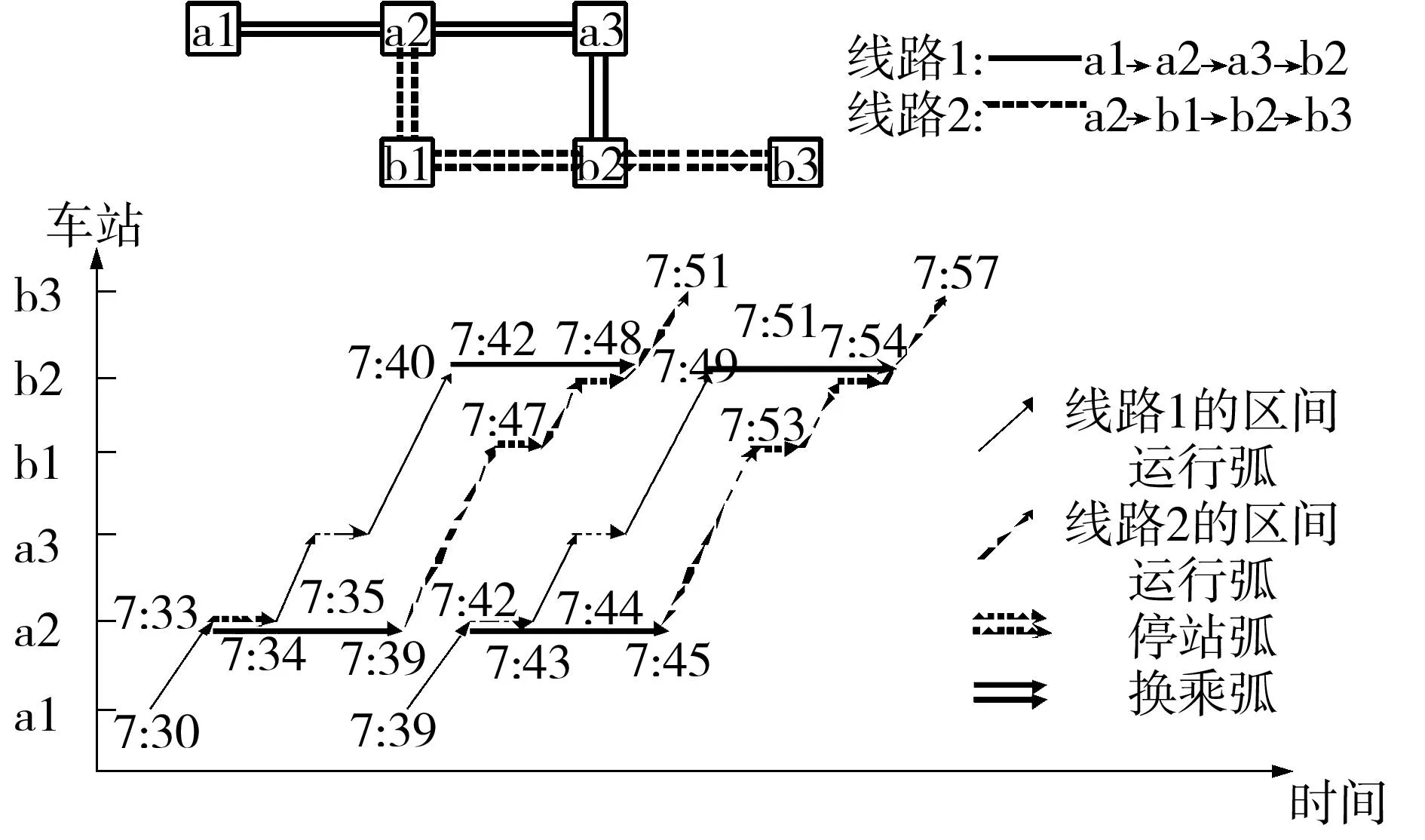
图1 时刻表扩展网络Fig.1 Schedule-expanded network
2有效时变扩展k短路径搜索算法
由于文中考虑正常运营情况下的城市地铁交通网络,为了保证有效时变扩展路径的无回路性质和可连通性质,在正常运营状态下,有效时变扩展路径应具备以下条件:
(1)属于同一线路区间运行弧不能间断性出现,即乘客在出行过程中不可能在同一条线路上的列车下车换乘至另一条线路,然后再换回这条线路;
(2)属于同一换乘车站的时变换乘弧不能同时出现在同一时变路径中,即乘客在出行过程中不可能利用同一个换乘车站换乘2次及以上;
(3)属于同一车站的时变扩展节点不能同时出现在同一时变路径中,即在一般情况下,乘客在出行过程中不会走“回头路”.

步骤1搜索出静态路径Rs,t中任意路径的经M次列车车次扩展的时变扩展路径.令迭代步数n=1.

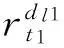
(3)按照换出的线路车次dli依据步骤2的方法往前遍历,每至换乘站扩展节点则按照满足乘客换乘时间小于换乘弧权值而搜索出的换出线路的前M个车次,直至遍历至终点t的扩展节点.将所有的时变弧连接,此时则获得经M次列车车次扩展的时变扩展路径.
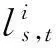
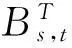
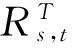
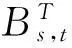
由于乘客在出行的过程中不会考虑OD间所有的时变k短路径,仅会考虑其中的一部分路径,该部分路径称为有效路径.为了确定有效的时变k短路径,文中定义有效时变k短路径应满足以下两个条件:
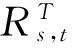
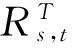
即路径集中的路径应满足下式:
(4)
式中,ttor为时间权值的乘客最大容忍绝对阈值,d1为时间权值的乘客最大容忍相对阈值.
3客流随机均衡分配模型
3.1 时变扩展路径的广义费用函数
文中考虑时刻表扩展网络上的时变路径其广义费用由以下3个部分组成:
(5)

(6)

(7)

(8)

(9)
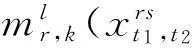
(10)

3.2 时刻表扩展网络的随机均衡分配模型
利用时刻表扩展的方法对城市地铁交通网络进行时间维扩展,可将客流的网络动态分配问题转化为网络客流加载过程.根据文献[14]的定义,时刻表扩展网络达到随机均衡状态(SUE)时,路径上的流量与费用满足下面的关系:
(11)

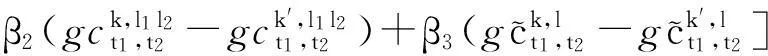
(12)
根据式(12),随着路径的流量逐渐增加,时变扩展路径的分配流量的分配比例保持不变,直到oidj间的某时变扩展路径分配流量超过其路径上列车的容量.因此,考虑列车容量限制条件下,时刻表扩展网络上的随机均衡分配最优化模型构建如下:
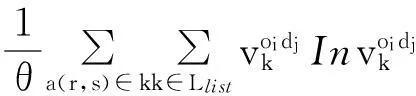
(13)
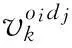
(14)
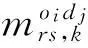
(15)

3.3 模型求解算法
对式(14)进行重构:

(16)

步骤1路网构建及初始化.

步骤2k短时变路径搜索.
根据前述时变扩展k短路径搜索算法计算研究网络的k短路径集,存储lk∈Ltlist.令迭代次数n=1.
步骤3迭代.
对于∀a(r,s)∈lk和∀oidj∈OD.分别计算式(17)、(18),获取每一步计算的路径分配流量和弧分配流量.
(1)对于∀a(r,s)∈lk,
(17)
(2)对于∀oidj∈OD,
(18)
令n=n+1.

步骤4收敛性判断.
收敛判断条件
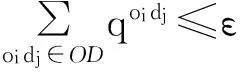
(19)
ε为预设的收敛误差,一般取一个充分小的正数,若不满足收敛判断条件,则返回步骤3,否则转步骤4.
步骤5结果输出.
对于∀a(r,s)∈lk,按照下式计算SUE条件下的路径分配流量和留乘延误时间费用.
(20)
4基本算例
为了验证模型计算的有效性,以北京地铁网络进行实际客流分配计算.截止至2014年11月份为止,北京地铁网络共包含17条运营线路,线路长度为465 km,281座开通车站,其中包含41座换乘车站,同时包含623个列车运行区间.
本算例中的分配时间段选取2014年4月4日早7:00~9:00,根据AFC数据分析,在这期间存在54 468个有效OD对,共1 095 835条乘客出行记录,基础的输入数据来源于北京地铁公司的公布数据及调查数据,主要包括列车运行时刻表、换乘站换乘走行时间和列车最大载客能力等,由于篇幅受限,文中只列出部分输入数据.
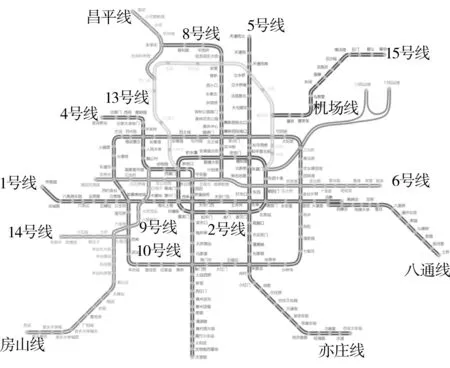
图2 北京地铁网络Fig.2 Beijing urban rail transit network

表1 部分输入数据Table 1 Parts of the input data

续表1
1)换乘站换乘时间;2)列车130%满载率下的载客人数.
相关参数通过统计方法[16]采用SPSS拟合,对于无实际数据支持的数据则采用既有研究[2,15]的参数值,相关参数取值见表2.

表2 模型中的参数取值Table 2 Values of the parameters in the model
根据地铁网络数据和时刻表数据,生成并存储时刻表扩展网络数据,采用上文提出的k短时变路径搜索算法,通过改进的MSA算法进行客流动态分配,计算可得以下结果:各线路各班次列车的乘车人数,各换乘站的换乘客流,各线路区间的客流留乘延误时间.下面对计算结果进行分析.
图3表示在θ=1时的算法收敛性.实际上在计算前25次迭代时,算法的迭代误差下降速率较快,至50次迭代时误差为0.98%,至100次(计算时间300 s)左右时迭代误差小于0.5%,说明算法具备较好的收敛性质.考虑到将模型实际应用于大规模的地铁,可以提高收敛误差,以适应大规模流量分配计算.

图3 θ=1时收敛次数的误差变化情况Fig.3 Changes in the error of convergence characteristics forθ=1
采用仿真推演的方法对客流分布的情况进行实时推演并展示客流路网分布的瞬时状态,可以模拟每个被分配乘客在地铁系统中的微观出行过程、车辆在路网中的运行过程.基于此,配套开发了地铁客流分配评估系统,并以此对地铁运营客流监控提供辅助决策支持.利用列车满载率指标展示在每个仿真统计步长的区间客流分布状态,通过绿、黄、橙、红4色分别表示区间满载率处于(0,70%),(70%,100%),(100%,120%),(120%,130%)时的情况.图4表示在7:30,8:00,8:30,9:00末的路网列车满载率的瞬时分布图.列车满载率的变化情况反映了线路不同方向的断面客流需求和拥挤状态,结合可视化的线路列车满载率情况,为地铁运营工作人员提供线路运力配置、运能调节提供决策依据:列车高满载率意味着该方向断面客流量大,需在满足列车周转的前提下提高线路的运能,增加运力资源;低满载率则意味着需在满足地铁服务质量的情况下降低运营成本,减少车体在路网中的周转运用.



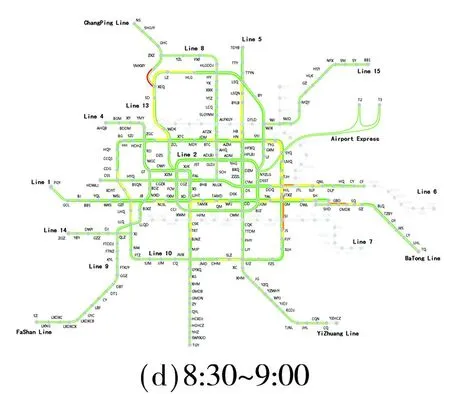
图4 北京地铁7:00~9:00的客流网络分布情况Fig.4 Passenger flow distribution in BURT network from 7:00 to 9:00 am
在θ=1时,列车运行区间的断面客流量分配结果与实际数据对比结果如图5所示.通过与实际调研数据对比,在考虑列车运输能力限制的条件下,模型推算的区间断面客流量与实际较为相符,模型的误差通过计算约为11.2%.
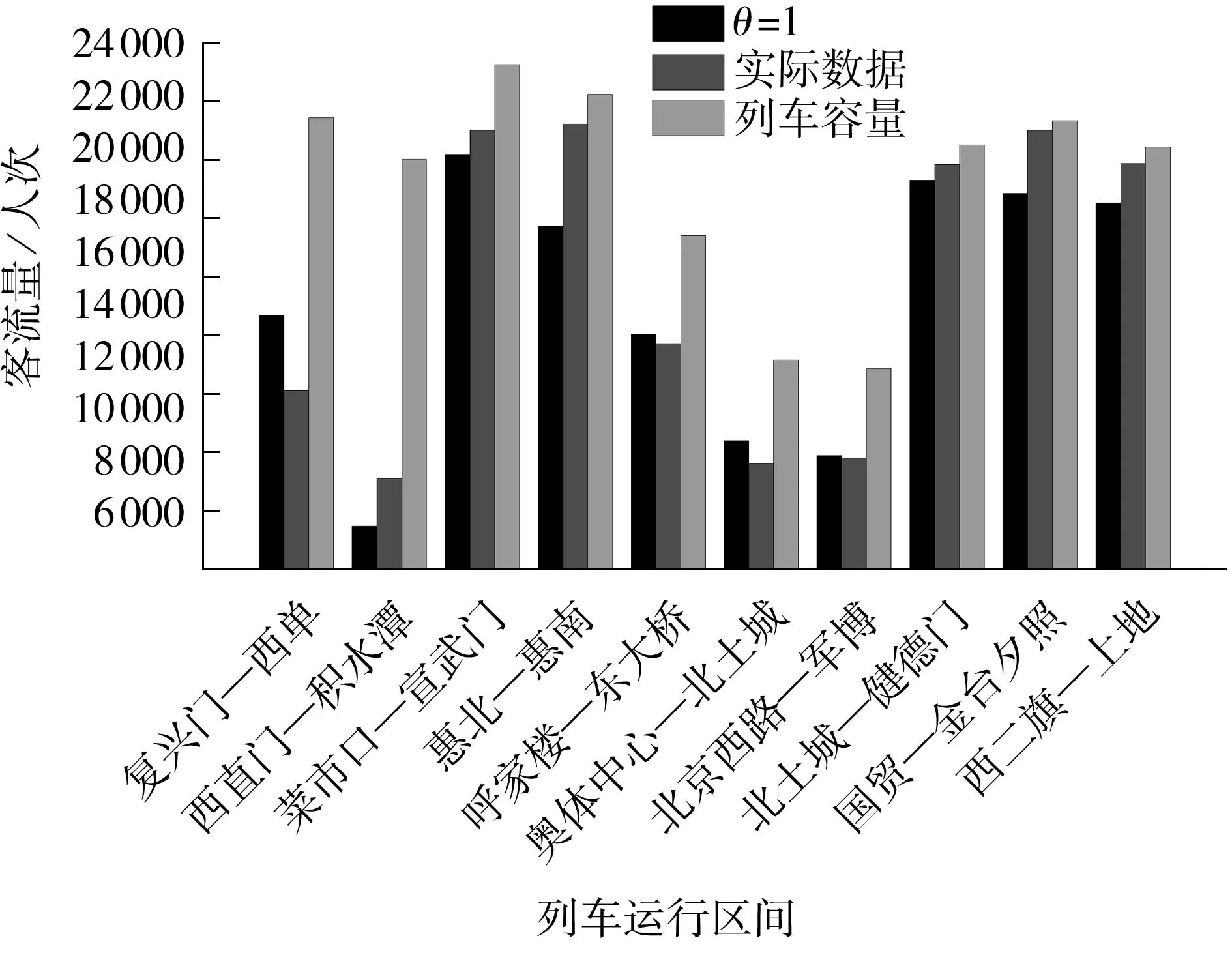
图5区间断面客流量的实际调研数据、模型计算值和区间通过能力比较
Fig.5Comparison of surveyed flows,computed flows and capacity in transit sections
进一步分析模型中参数对于分配的敏感性问题.θ取值不同将反映乘客对于路径选择的敏感度变化情况.图中纵轴表示不同路径广义费用归一化的值,根据图6不难看出,当θ取值越小表示乘客对于路径广义费用变化敏感度不大,乘客对于路径选择的概率偏离值较平缓,当θ取值越大则表示乘客对于路径选择具有较大的敏感性,细微的路径费用差别会引起较大的选择比例变化.通过改变θ值,计算θ=0.1~20.0时输出模型推算的乘客留乘延误时间和区间断面客流量,如表3和图7所示.

图6 θ取值不同时的路径选择概率偏离值变化趋势Fig.6 Changes in the deviation of path choice probability for different values of the parameter

表3 θ取值不同时的乘客留乘延误时间Table 3 Overload delays of transit sections for different values of the parameterθ

图7 θ取值不同时的区间断面客流量计算结果Fig.7 Impacts ofθin assignment results
通过表3可以看出留乘延误时间随着θ值增大而变大.这是因为随着θ值增大,意味着乘客对于网络中不同路径上的列车到发时间、拥挤状态等实际路网信息更熟悉.当客流分配至随机平衡状态时,乘客总是会选择感知费用最小的路径.由于群体的共同选择,乘客总是选择最先到达的列车,因此在列车容量达至能力上限时,乘客被迫选择后续列车,从而增加了留乘延误时间.
由于更大的θ值意味着乘客对于路网的熟悉度增加,当θ值较小时表示乘客会选择高费用的路径,进而产生选择偏差.图7中不同的区间断面量与实际数据对比表明,当θ取值范围在[1,5]时,相对误差较小,约为9.5%~11.2%.
5结语
随着城市地铁交通网络规模的不断增大,客流的非线性叠加效果不断加强所引起乘客出行选择的变化,将对网络化运营管理提出更高的要求.因此建立准确可行的城市地铁交通网络客流分配模型,实现网络客流分布的科学分析和合理评估是城市地铁交通网络化运营管理的客观需求,对社会、经济和城市发展具有重要的意义.鉴于城市地铁交通是基于时刻表的运输方式,列车开行计划和列车能力限制是网络客流分布的重要影响因素,文中在充分考虑这些因素的同时通过构建扩展网络,基于随机用户均衡理论构建了客流分配模型并设计求解算法,并给出了实例分析.实例验证了模型的科学可行性.在此基础上,笔者将对模型中涉及的参数验证和乘客行为选择因素分析(如列车到发时间选择等)进行进一步的研究.
参考文献:
[1]四兵锋,毛保华,刘智丽.无缝换乘条件下城市轨道交通网络客流分配模型及算法 [J]. 铁道学报,2007,29(6):12-18.
Si Bing-feng,Mao Bao-hua,Liu Zhi-li.Passenger flow assignment model and algorithm for urban railway traffic network under the condition of seamless transfer [J].Journal of the China Railway Society,2007,29(6):12-18.
[2]吴祥云,刘灿齐.轨道交通客流量均衡分配模型与算法 [J].同济大学学报:自然科学版,2004,32(9):1158-1162.
Wu Xiang-gun,Liu Can-qi.Traffic equilibrium assignment model specially for urban railway network [J]. Journal of Tongji University:Natural Science,2004,32(9):1158-1162.
[3]徐瑞华,罗钦,高鹏.基于多路径的城市轨道交通网络客流分布模型及算法研究 [J].铁道学报,2009,31(2):110-114.
Xu Rut-hua,Luo Qin,Gao Peng.Passenger flow distribution model and algorithm for urban rail transit network based on multi-route choice [J].Journal of the China Railway Society,2009,31(2):110-114.
[4]Babazadeh A,Aashtiani H Z.Algorithm for equilibrium transit assignment problem [J].Transportation Research Record:Journal of the Transportation Research Board,2005,1923(1):227-235.
[5]Kurauchi F,Bell M G H,Schmöcker J D.Capacity constrained transit assignment with common lines [J].Journal of Mathematical Modelling and Algorithms,2003,2(4):309-327.
[6]Nielsen O A.A stochastic transit assignment model considering differences in passengers utility functions [J].Transportation Research Part B:Methodological,2000,34(5):377-402.
[7]Poon M H,Wong S C,Tong C O.A dynamic schedule-based model for congested transit networks [J].Transportation Research Part B:Methodological,2004,38(4):343-368.
[8]Wilson N H M,Nuzzolo A.Schedule-based modeling of transportation networks [M].Berliu:Springer,2008.
[9]Schmöcker J D,FonzoneA,Shimamoto H,et al.Frequency-based transit assignment considering seat capacities [J].Transportation Research Part B:Methodological,2011,45(2):392-408.
[10]Nuzzolo A,Crisalli U,Rosati L.A schedule-based assignment model with explicit capacity constraints for congested transit networks [J].Transportation Research Part C:Emerging Technologies,2012,20(1):16-33.
[11]Cascetta E,Cantarella G E.A day-to-day and within-day dynamic stochastic assignment model [J].Transportation Research Part A:General,1991,25(5):277-291.
[12]Hamdouch Y,Lawphongpanich S.Schedule-based transit assignment model with travel strategies and capacity constraints [J].Transportation Research Part B:Methodological,2008,42(7):663-684.
[13]Zhou W T,Han B M,Yin H D.Study on thek-shortest paths searching algorithm of urban mass transit network based on the network characteristics [J].Applied Mechanics and Materials,2014,505:689-697.
[14]Lam W H K,Gao Z Y,Chan K S,et al.A stochastic user equilibrium assignment model for congested transit networks [J].Transportation Research Part B:Methodological,1999,33(5):351-368.
[15]Xu W,Miao L,Lin W H.Stochastic user equilibrium assignment in schedule-based transit networks with capacity constraints [J].Discrete Dynamics in Nature and Society,2012,1(1):1-15.
[16]四兵锋,高自友.交通运输网络流量分析与优化建模 [M].北京:人民交通出版社,2013.
Passenger Flow Assignment Model of Subway Networks Under Train Capacity Constraint
ZhouWei-teng1HanBao-ming1,2
(1.School of Traffic and Transportation, Beijing Jiaotong University,Beijing 100044,China;2. State Key Laboratory
of Rail Traffic Control and Safety,Beijing Jiaotong University,Beijing 100044,China)
Abstract:The passenger flow assignment of subway networks plays an important role in the operation and management of urban rail transit networks.As the influence of the train capacity constraint on the passenger flow assignment in a schedule-based network is seldom taken into account in relevant literature,this paper constructs a dynamic assignment model of passenger flows under the condition of the stochastic user equilibrium,and designs a solution algorithm by establishing a schedule-expanded network and by designing correspondingk-shortest path search algorithm.Moreover, the congestion and overload delay under the train capacity constraint are also taken into account.Then,the proposed model is verified by a numerical example in Beijing subway networks,and the parameter sensitivity is analyzed.The results show that the proposed model is of a rapid convergence and a higher degree of accuracy with a relative error of 9.5%~11.2%,which can meet the requirements of analyzing and estimating the passenger flow distribution in a large-scalesubway network.
Key words:subways;passenger flow assignment;schedule;traincapacity;overload delay
中图分类号:U 239.5
doi:10.3969/j.issn.1000-565X.2015.08.019
文章编号:1000-565X(2015)08-0126-09
作者简介:周玮腾(1988-),男,博士,主要从事城市轨道交通运输规划与管理研究.E-mail: zwt_bjtu@126.com†通信作者: 韩宝明(1963-),男,教授,博士生导师,主要从事运输组织现代化研究.E-mail: bmhan@bjtu.edu.cn
*基金项目:北京市自然科学基金资助项目(9132015);北京交通大学中央高校基本科研业务费专项资金资助项目(2015JBM046);北京高等学校青年英才计划(YETP0555);北京交通大学基本科研业务费资助项目(2014JBM058)
收稿日期:2014-12-01
Foundation item: Supported by the Beijing Municipal Natural Science Foundation(9132015)
