惯性系下平台惯导传递对准方法

高　伟, 单　为, 徐　博, 程正生

(1.哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001;

2.中国船舶重工集团707研究所, 江西 九江 332000)



惯性系下平台惯导传递对准方法

高伟1, 单为1, 徐博1, 程正生2

(1.哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001;

2.中国船舶重工集团707研究所, 江西 九江 332000)

摘要：由于导弹的高速旋转导致其内部的子惯导平台难以施矩,不能跟踪地理系,在发射前需要使子惯导平台跟踪惯性系,而主惯导则一直跟踪地理系。针对这一情况的传递对准应用问题给出了相应的解决办法。首先介绍了跟踪惯性系平台惯导的工作原理,然后针对这种情况,提出了2种惯性系下传递对准的方法,分别是平台惯性系以及地心惯性系下的速度匹配。经过对比分析,仿真结果说明平台惯性系下的方位失准角精度不高,而地心惯性系下在3个方向上都达到了误差小于1′的精度,是一种可行的对准方法。

关键词：传递对准; 平台惯导; 惯性系; 速度匹配; 卡尔曼滤波

0引言

初始对准技术是惯导系统的关键技术之一,它是惯导系统正常工作的基本条件[1-6]。惯导系统传递对准是指当载体载弹航行时,弹体上需要对准的导航系统(称为子惯导系统)利用载体上已对准好的惯导系统(称为主惯导系统)的信息进行对准的一种方法[7]。对于机载武器的捷联惯导系统来说,是一种有效的方法,可以极大的提高武器系统的反应速度和防区外攻击能力[8-11]。而装有平台掼导的导弹在发射前为了解决高速旋转时的平台施矩问题,要进入“断调平”状态,即跟踪平台惯性系,在惯性空间只受陀螺漂移影响,而平台惯性系指的是断调平状态初始时刻凝固在惯性空间的平台系。而这一方面的问题其实可以看做为惯性系下的传递对准问题,文献[12]通过建立计算惯性系的方法,推导了计算惯性坐标系下传递对准动态误差模型;文献[13]提出了发射点惯性系下传递对准的模型和算法;文献[14]提出了基于惯性参考系的四元数传递对准方法。目前,基于惯性坐标系为基准的对准方法正在得到逐步应用和完善,已应用于船用惯导系统系泊状态下的自对准和陆用车辆行进间对准中[12-17]。但是这些方法都是基于捷联惯导的,而且针对工作在“断调平”状态的子惯导与工作在地理系的主惯导之间的传递对准问题,国内外的文献几乎没有涉及。

本文针对工作在“断调平”状态的子惯导与依旧跟踪地理系的主惯导之间的传递对准问题给出了2种惯性下传递对准办法:一是在平台惯性系下完成传递对准;二是在地心惯性系下完成传递对准。考虑到远程导弹发射时角运动较小的操作环境,可以忽略杆臂效应,并且平台惯导具有没有挠曲变形影响的优势,本文采用了速度匹配的传递对准方法,所以时间延迟的影响也很小,也可以忽略不计。之后采用卡尔曼滤波进行滤波估计,比较了这2种方法,分析了仿真结果,给出了结论。在第1节中,本文将介绍“断调平”状态下平台惯导的导航方式,以及分析这种情况时的传递对准应用问题;第2节和第3节将分别介绍以上2种不同坐标系下的方法;第4节中给出仿真实验,最后分析结果并说明原因。

1平台惯导跟踪惯性系原理

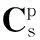
(1)

图1　“断调平”状态平台惯导工作方式

对于平台式惯导系统来说,初始对准就是要知道平台坐标系与导航坐标系之间的误差角大小[17-19],而本文阐述的就是作为子平台惯导进入“断调平”状态之后的传递对准应用问题,需要补偿的就是主、子惯导平台之间的误差角为φ,从而获得子惯导平台相对地理系的真实姿态,并且这个误差角是实时变化的,写做矩阵形式为

(2)

图2为导航坐标系在地球坐标系的投影。由图2可得

(3)

(4)

图2 导航坐标系在地球坐标系的投影

n0为子惯导进入断调平状态时,主惯导的平台系,且它凝固于惯性空间中,相对惯性系i保持不动,也记为m,称作主惯导平台惯性系,φn0,λn0分别为主惯导当时所在纬度与经度,有

(5)

将主惯导平台惯性系与子惯导平台的误差角设为φi,考虑子惯导陀螺漂移有

(6)

式中，ε为陀螺漂移,而式(2)中的Csm正是此误差角的矩阵形式

(7)

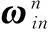
(8)

(9)

所以我们此时传递对准的任务即是估计出Csm的大小,而将主惯导所得到的比力fn经过下面转换

fm=Cmnfn

(10)

从而就能投影到平台惯性系上利用

(11)

建立误差方程,估计出φι,然后再利用式(8)更新失准角矩阵,最终获得误差角φ。

与式(9)同理,我们可以通过

(12)

的方法从而得到

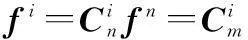
(13)

以及

(14)

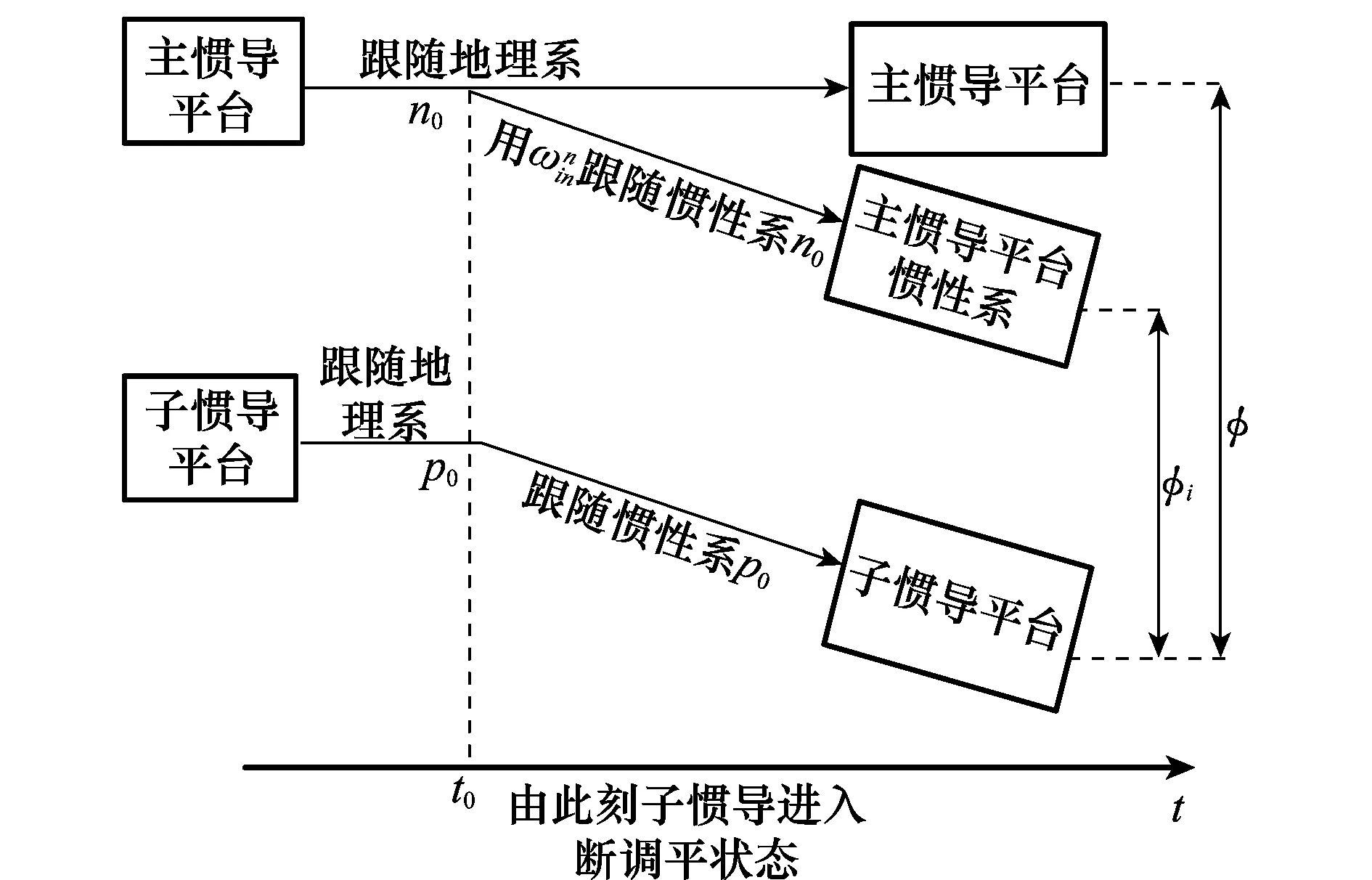
图3　主、子惯导进入断调平状态说明

2平台惯性系下传递对准模型

应用式(9)与式(10)可以得到主惯导在平台惯性系m下的比力fm,则定义在此惯性系下的速度有

(15)

(16)

且gm为重力加速度矢量在平台惯性系下投影gm=Cmn·gn。则对子惯导也有

(17)

且gs=Cmn·gn。并且由式(11),对式(16)与式(17)相减,可得

(18)

平台惯导无挠曲变形,则主、子平台惯性系的失准角φi将只受子惯导的陀螺漂移影响,根据式(6)可得

(19)

由式(18)与式(19)就可建立平台惯性系下的状态观测方程,滤波模型为

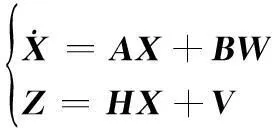
(20)

选取状态量

X=

则有

V为测量噪声,本文采用速度匹配,以主、子惯导平台惯性系上的速度差为观测量,然后用卡尔曼滤波估计出状态量中的φi,最后用式(8)就可以得到子惯导平台系与主惯导平台系之间的夹角φ。

3地心惯性系下传递对准模型

通过式(13)以及式(14)可以得到主、子惯导在地心惯性系下的比力fi与fj,并且由式(15)同理可得

(21)

(22)

(23)

根据式(23),将式(21)与式(22)相减可得

(24)

平台惯导无挠曲变形,则主、子平台惯性系的失准角φi将只受子惯导的陀螺漂移影响,根据式(6)可得

(25)

由式(24)与式(25)就可建立平台惯性系下的状态观测方程,选取状态

X=

滤波模型与式(20)相同,则

V为测量噪声,采用速度匹配以主、子惯导地心惯性系上的速度差为观测量,然后用卡尔曼滤波估计出状态量中的φi,最后用式(8)就可以得到子惯导平台系与主惯导平台系之间的夹角φ。

4仿真实验

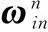
仿真条件1:地点选为哈尔滨,初始纬度φ=45.779 6°,初始经度λ=126.670 5°,主、子惯导平台的初始失准角,即子惯导进入“断调平”状态初始时刻的失准角为φx=15′,φy=15′,φz=30′,且根据第1节内容可知此时φix,φix,φix的初始值也分别为15′,15′,30′。设陀螺常值漂移为0.01(°)/h,加速度计零偏为10-4g0,采样频率为0.1 s,且主、子惯导都为静止的条件下。

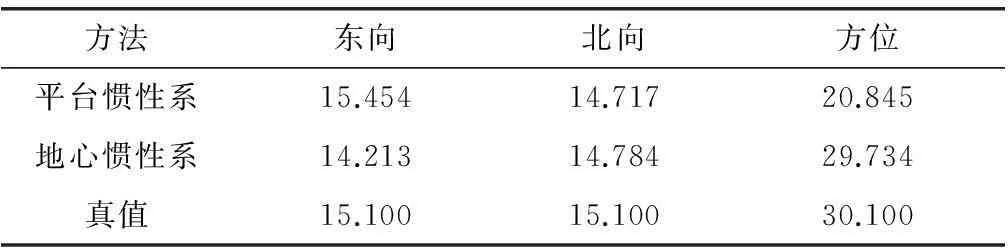
仿真结果如图4～图6以及表1所示。

图4　静基座下2种方法在X轴方向仿真曲线

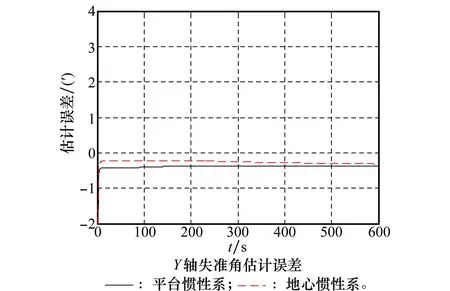
图5　静基座下2种方法在Y轴方向仿真曲线

图6　静基座下2种方法在Z轴方向仿真曲线

(′)

仿真结果如图7～图9以及表2所示。

图7　动基座下2种方法在X轴方向仿真曲线

(′)

图8　动基座下2种方法在Y轴方向仿真曲线

图9　动基座下2种方法在Z轴方向仿真曲线

从以上仿真图以及表格内参数可知,2种方法的仿真结果是不一样的,具体可以归纳为以下几点。

(1) 静态下,平台惯性下的速度匹配能够估计3个方向上的误差角,在水平方向上的估计精度很高,但是方位上精度不高,不能保证传递对准的精确性。但是如果在动态下,将会提高方位误差角的可观测度,将误差值从10′降低到了2′,提高了精度。

(2) 地心惯性下的速度匹配在静态以及S机动情况下,都能够估计出3个方向上的误差角,且都达到了小于1′的精度。虽然水平方向上的精度比平台惯性系下的精度略低,而在方位上的精度却很大的超越了平台惯性系下速度匹配的精度。所以此条件下地心惯性系相比与平台惯性系是一种更好的方法。

简单分析原因,可以认为的是,由于主、子惯导所测的比力主要受重力加速度影响,而平台惯性系3个方向上比力分量偏差过大,所以方位上的精度不高,而通过合适的机动方式使得分量偏差减小,从而可以提高方位的可观测度。而通过将误差方程建立在地心惯性系下,可以使得重力加速度在3个方向上分量的偏差能够大大减小,从而提高了方位失准角的精度。

5结论

本文分析了“断调平”状态下平台惯导的工作方式,并且针对主惯导依旧工作在地理系子惯导工作在“断调平”状态的情况,给出了2种传递对准速度匹配的基本模型。并且都进行了仿真实验,比较了这2种方法的仿真结果,分析了估计精度差异的原因。最后说明此条件下,地心惯性系相比平台惯性系是一种更好的传递对准方法。

参考文献：

[1] Wan D J, Fang J C.Inertialnavigationinitialalignment[M]. Nanjing:Southeast University Press,1998:1-10.(万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社, 1998:1-10.)

[2] Liu X X, Xu X S, Liu Y T. A fast and high-accuracy transfer alignment method between M/S INS for ship based on iterative calculation[J].Measurement, 2014, 51, 297-309.

[3] Wu M P, Wu Y X, Hu X P. Optimization-based alignment for inertial navigation systems:theory and algorithm[J].AerospaceScienceandTechnology, 2011, 15(1), 1-17.

[4] Gao S S, Wei W H, Zhong Y M. Rapid alignment method based on local observability analysis for strapdown inertial navigation system[J].ActaAstronautica, 2014, 94(2), 790-798.

[5] Choukroun D, Bar-Itzhack I Y, Oshman Y. Novel quaternion Kalman filter[J].IEEETrans.onAerospaceandElectronicSystems, 2006, 42(1),174-190.

[6] Kain J E, Cloutier J R. Rapid transfer alignment for tactical weapon applications[C]∥Proc.oftheAIAAGuidance,NavigationandControlConference, 1989,1290-1300.

[7] Yang D F, Wang S C, Li H B. Performance enhancement of large-ship transfer alignment:a moving horizon approach[J].TheJournalofNavigation, 2013, 66(1),17-33.

[8] Chen Y, Zhao Y. New rapid transfer alignment method for SINS of airborne weapon systems[J].JournalofSystemsEngineeringandElectronics, 2014,25(2), 281-287.

[9] Kang T Z, Fang J C, Wang W. Quaternion-optimization based in-flight alignment approach for airborne POS[J].TransactionsonInstrumentationandMeasurement,2012,61(11):2916-2923.

[10] Groves P D. Optimising the transfer alignment of weapon INS[J].TheJournalofNavigation, 2003, 56(2), 323-335.

[11] Ali J, Mirza M R U B. Initial orientation of inertial navigation system realized through nonlinear modeling and filtering[J].Measurement, 2011, 44(5), 793-801.

[12] Wang Q Z, Fu M Y, Xiao H, et al. Rapid transfer alignment method based on inertial reference frame[J].JournalofChineseInertialTechnology,2012,(2):168-172.(王清哲,付梦印,肖烜,等. 基于惯性参考系基准的快速传递对准方法[J]. 中国惯性技术学报,2012,(2):168-172.)

[13] Han X P, Mu R J, Cui N G. Comparison between transfer alignments of inertial navigation system in two coordinates[J].JournalofChineseInertialTechnology, 2010,(3):272-278.(韩鹏鑫,穆荣军,崔乃刚. 两种坐标系下惯导传递对准效果比较[J]. 中国惯性技术学报,2010,(3):272-278.)

[14] Chen Y, Zhao Y, Li Q S. Linear filtering transfer alignment method based on inertial reference frame[J].SystemsEngineeringandElectronics,2013, 35(12):2577-2581.(陈雨,赵剡,李群生. 基于惯性参考系线性滤波传递对准方法[J]. 系统工程与电子技术, 2013, 35(12):2577-2581.)

[15] Lian J X, Wu W Q, Wu M P, et al. SINS initial alignment algorithm for marching vehicles[J].JournalofChineseInertialTechnology, 2007,(2):155-159.(练军想,吴文启,吴美平,等. 车载SINS行进间初始对准方法[J]. 中国惯性技术学报, 2007,(2):155-159.)

[16] Yan G M, Weng J, Bai L, et al. Initial movement alignment and position determination based on inertial reference frame[J].SystemsEngineeringandElectronics, 2011, 33(3):618-621.(严恭敏,翁浚,白亮,等.基于惯性参考系的动基座初始对准与定位导航[J].系统工程与电子技术,2011,33(3):618-621.)

[17] Gao W, Ben Y Y, Zhang X, et al. Rapid fine strapdown INS alignment method under marine mooring condition[J].IEEETrans.onAerospaceandElectronicSystems, 2011, 47(4):2887-2895.

[18] Harris R A, Wakefield C D. Coordinate alignment for elastic bodies[C]∥Proc.oftheIEEENationalAerospaceElectronicConference, 1977,5,665-670.

[19] Dai H D, Dai S W, Cong Y C. Rapid transfer alignment of laser SINS using quaternion based angular measurement[J].Optik, 2013,124(20):4363-4368.

高伟(1977-),男,教授,博士研究生导师,主要研究方向为导航、制导与控制。

E-mail:gaow@hrbeu.edu.cn

单为(1992-),男,硕士研究生,主要研究方向为导航、制导与控制。

E-mail:1165077074@qq.com

徐博(1983-),男,硕士研究生导师,博士,主要研究方向为导航、制导与控制。

E-mail:xubocarter@sina.com

程正生(1968-),男,高级工程师,主要研究方向为导航、制导与控制。

E-mail:xiaogang_v@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141120.2115.013.html

Transfer alignment of platform inertial navigation

in the inertial coordinate

GAO Wei1, SHAN Wei1, XU Bo1, CHENG Zheng-sheng2

(1.SchoolofAutomation,HarbinEngineeringUniversity,Harbin150001,China;

2.Institute707ofChinaShipbuildingIndustryGroup,Jiujiang332000,China)

Abstract:Due to high speed rotation of the missile, the internal slave platform inertial navigation system cannot be torqued to track the geographical coordinate, so it is necessary to make the slave navigation platform track the inertial coordinate before the missile launch, while the master platform inertial navigation system still tracks the geographical coordinate. To solve the transfer alignment problem of the situation, this paper puts forward the corresponding solutions. the principle of the platform inertial navigation system which tracks the inertial coordinate is introduced firstly, then the transfer alignment methods in two kinds of inertial coordinate (the platform inertial coordinate and the geocentric inertial coordinate) are proposed. The simulation results show that the precision of the azimuth misalignment angle in the platform inertial coordinate is not preferable,however, the misalignment angle in the geocentric inertial coordinate achieves an accuracy of less than 1′, which shows that it is a feasible method of alignment.

Keywords:transfer alignment; platform inertial navigation system; inertial coordinate; velocity matching; Kalman filtering

作者简介：

中图分类号：U 666.12+1

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.27

基金项目：国家自然科学基金(61203225)；中央高校基本科研业务费专项基金(HEUCF110427)；国家博士后基金(2012M510083)；黑龙江省青年科学基金(QC2014C069)资助课题

收稿日期：2014-06-04；修回日期：2014-10-29；网络优先出版日期：2014-11-20。