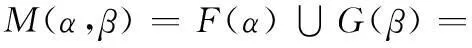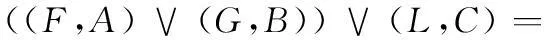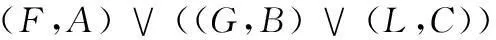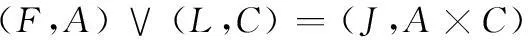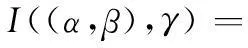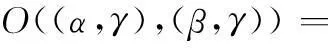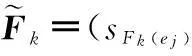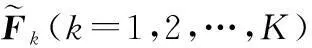区间三角模糊软集及其动态决策方法

陈孝国， 杜　红

(1. 中国矿业大学(北京)力学与建筑工程学院， 北京 100083；

2. 黑龙江科技大学理学院， 黑龙江 哈尔滨 150022)



区间三角模糊软集及其动态决策方法

陈孝国1,2， 杜红2

(1. 中国矿业大学(北京)力学与建筑工程学院， 北京 100083；

2. 黑龙江科技大学理学院， 黑龙江 哈尔滨 150022)

摘要：为完善模糊软集理论，提出区间三角模糊软集的概念，并讨论其相关运算及性质。建立基于区间三角模糊软集的动态决策模型，其中，时间权重采用指数衰减方法进行确定，利用集成的思想定义了区间三角模糊软集算术加权平均算子，将不同时刻的区间三角模糊软集集成为综合区间三角模糊软集。给出不同对象选择值和决策值的求解公式，根据决策值大小来实现最优决策。最后总结出方法的具体步骤，并通过实例说明具体应用。

关键词：区间三角模糊软集； 集成； 动态决策； 模糊软矩阵

0引言

目前处理不确定性问题的方法主要有概率论[1]、区间数理论[2]、模糊集理论[3]以及粗糙集理论[4]。但是，上述这些理论和方法都普遍存在参数化不够充分的缺点和不足[5]。因此，文献[5]在对现有不确定性数学理论对比分析基础之上，提出了一个全新、有效的数学概念软集。软集的最大优势是能够借助灵活的参数化方法来更加细腻地描述客观事物的不确定性，然而随着研究的深入，针对事物的属性值以模糊数、区间数以及直觉模糊数描述时，经典软集显得无能为力，所以国内外许多学者对其扩展研究进行了广泛的探讨。文献[6]在对软集和模糊集的相关性质研究基础上提出了模糊软集理论，并给出了交、并、补等运算。文献[7]又进一步将软集扩展，给出了更具应用前景的直觉模糊软集概念。文献[8]在对软集和区间值模糊集研究的基础上提出了区间值模糊软集理论，并探讨了对偶律和结合律等相关定理。文献[9]在直觉模糊软集的基础上进行了更深入的研究，定义了区间值直觉模糊软集。文献[10]提出了粗糙软集。文献[11-12]首次提出基于软集和模糊软集的决策方法和步骤，并在实例分析中采用粗糙集理论对事物属性进行约简，文献[13]对文献[12]决策方法的错误进行了探讨。文献[14]重新定义了Molodtsov所提出的软集概念及其运算性质，并且给出了一种基于软集的uni-int决策方法。文献[15]给出了软矩阵定义，并得到了许多有应用价值的矩阵运算结论，最后利用max-min软矩阵决策方法对实例进行了分析。文献[16-17]分别对软集进行了扩展研究，同时在决策时提出设定阈值向量构造水平软集，将不同类型软集转化为经典软集，再通过不同对象机会值的大小得到最优决策。文献[18-19]年给出了三角模糊软集和梯形模糊软集的定义及其相关运算性质，并建立了相应的决策模型。

上述研究虽然对软集的扩展进行了广泛的探讨，但是对区间三角模糊软集的研究文献却相对较少，同时，上述关于决策的研究基本都是静态的，实际问题中往往需要动态进行分析，因此在模糊软集决策中引入时间变量是必要的。基于此，本文提出区间三角模糊软集的定义，并探讨相关运算性质。建立考虑时间变量的动态区间三角模糊软集决策模型，时间权重采用文献[20]中指数衰减方法确定。利用集成的思想[21]定义区间三角模糊软集的算术加权平均算子，并给出动态区间三角模糊软集的集成定理。同时借鉴文献[8，18]所提出的决策思路，定义一种基于区间三角模糊软集的选择值和决策值求解公式，并用于决策分析中。

1区间三角模糊数及其性质

如果0

定义 2设s=[(a-,a+);b;(c-,c+)]和t=[(m-,m+);h;(k-,k+)]是两个区间三角模糊数，如果a-≤ m-，a+≤ m+，b ≤ h，c-≤ k-，c+≤ k+，则称s ≤ t。

定义 3设s=[(a-,a+);b;(c-,c+)]和t=[(m-,m+);h;(k-,k+)]是两个区间三角模糊数，则

(1)

(2)

定义 4设 t=[(m-,m+);h;(k-,k+)]是一区间三角模糊数，则t的补集为

(3)

定义 5设s=[(a-,a+);b;(c-,c+)]和t=[(m-,m+);h;(k-,k+)]是两个区间三角模糊数，常数k>0，则

b+h-bh;

(4)

(5)

定义3～定义5能够保证规范区间三角模糊数运算的封闭性。

2区间三角模糊软集及其性质

定义 6设U为论域，E为参数集，Γ(U)表示论域U上所有区间三角模糊集，A⊆E，称(F,A)为论域U上的一个区间三角模糊软集，其中映射F：A→Γ(U)。即对∀e∈A，有

(6)

式中，sF(e)(x)是F(e)中x所对应的区间三角模糊数。

定义 7设(F,A)和(G,B)是论域U上的两个区间三角模糊软集，那么当且仅当A⊆B且对∀e∈A，F(e)是G(e)的区间三角模糊子集。即对∀x∈U，F(e)和G(e)中x所对应的区间三角模糊数sF(e)(x)和sG(e)(x)满足

如果(G,B)是(F,A)的区间三角模糊软子集，那么(F,A)就是(G,B)的区间三角模糊软父集。

定义 9设(F,A)为论域U上的一个区间三角模糊软集，称(F,A)c=(Fc,A)为(F,A)的补集，其中映射Fc：A→Γ(U)，即对∀e ∈A，有

(7)

式中，sF(e)(x)是F(e)中x所对应的区间三角模糊数。

由定义9可以看出，显然

定义 10设(F,A)和(G,B)是论域U上的两个区间三角模糊软集，称(F,A)∧(G,B)为它们的“AND”运算，且(F,A)∧(G,B)=(H,A×B)，即对∀(α,β)∈A×B，有

(8)

式中，sF(α)(x)和sG(β)(x)分别是F(α)和G(β)中x所对应的区间三角模糊数。

定义 11设(F,A)和(G,B)是论域U上的两个区间三角模糊软集，称(F,A)∨(G,B)为它们的“OR”运算，且(F,A)∨(G,B)=(M， A×B)，即对∀(α,β)∈A×B，有

(9)

式中，sF(α)(x)和sG(β)(x)分别是F(α)和G(β)中x所对应的区间三角模糊数。

定理 1设(F,A)和(G,B)是论域U上的两个区间三角模糊软集，则有

(10)

(11)

证明设(F,A)∧(G,B)=(H,A×B)，则

并且

对∀(α,β)∈A×B，有

所以((F,A)∧(G,B))c=(F,A)c∨(G,B)c成立。

证毕

式(11)的证明过程类似。

定理 2设(F,A)、(G,B)和(L,C)是论域U上的3个区间三角模糊软集，则有

(12)

(13)

证明设(F,A)∧(G,B)=(H,A×B)

对∀(α,β)∈A×B，γ∈C，有

式中，sF(α)(x)，sG(β)(x)和sL(γ)(x)分别是F(α)，G(β)和L(γ)中x所对应的区间三角模糊数。

对∀(β,γ)∈B×C，∀α∈A，有

所以((F,A)∧(G,B))∧(L,C)=(F,A)∧ ((G,B)∧(L,C))成立。

证毕

式(13)的证明过程类似。

定理 3设(F,A)、(G,B)和(L,C)是论域U上的3个区间三角模糊软集，则有

(14)

(15)

证明设(F,A)∧(G,B)=(H,A×B)

对∀(α,β)∈A×B，γ∈C，有

对∀(α,γ)∈A×C，∀(β,γ)∈B×C，有

所以((F,A)∧(G,B))∨(L,C)=((F,A)∨(L,C))∧((G,B)∨(L,C))成立。

证毕

式(15)的证明过程类似。

3区间三角模糊软集的决策方法

3.1时间权重的确定

文献[20]提出采用指数衰减模型来确定时间权重，基本思想是不同时刻决策者所掌握的信息是不同的，离最终决策时刻越近则掌握决策信息越多，时间权重就越大，反之就越小。

本文只考虑时间为离散时的情况，设时间集T={1,2,…,K}，t∈T，则t时刻的权重为

(16)

式中，λ为衰减系数。

3.2区间三角模糊软集的集成方法

借鉴文献[21]的集成思想，可以类似定义区间三角模糊软集的算数加权平均算子，将不同时刻的区间三角模糊软集集成为综合区间三角模糊软集。文献[15]已经指出，模糊软集与模糊软矩阵一一对应，因此讨论区间三角模糊软集的集成方法就转化为研究区间三角模糊软矩阵的集成。

(17)

(18)

(19)

(20)

根据定义12和定义13可以看出定理4的证明是明显的。

3.3决策方法

(21)

i=1,2,…,m；j=1,2,…,n；k=1,2,…,K。

文献[8，18]针对区间模糊软集和三角模糊软集中的决策问题，均采用了选择值和决策值进行研究。本文借助该思路，给出论域中xi基于区间三角模糊软集的选择值μi和决策值ηi，表示为

(22)

(23)

3.4决策步骤

设论域U={x1,x2,…,xm}，参数集A={e1,e2,…,en}，时间集T={1,2,…,K}，时间权重向量为w=(w1,w2,…,wK)，根据上述讨论，可以得到区间三角模糊软集的动态决策步骤。

步骤 1根据决策者所掌握的信息确定衰减系数λ，利用式(16)计算各时刻权重。

步骤 2利用式(20)将不同时刻的区间三角模糊软矩阵集成为综合区间三角模糊软矩阵。

步骤 3利用式(22)和式(23)分别计算论域中每个元素对应的选择值和决策值。

步骤 4根据决策值的大小进行决策分析，最大决策值对应的元素最优。

4实例分析

某运载火箭技术研究院考虑从4家关键原材料特制钛合金供应企业{x1,x2,x3,x4}中选择一家进行长期合作，首先要求供应企业提供的产品质量要绝对可靠，随着航天科技的发展，供应企业要具有持续的科技创新能力，并与运载火箭技术研究院的战略目标匹配相一致。所以对特制钛合金供应企业的考察期设定为最近3年，决策者分别从企业信誉(e1)、企业持续科技创新能力(e2)和战略目标匹配(e3)三个方面逐年进行考察，评价结果以区间三角模糊软集的形式给出，如表1～表3所示。

表1　第1年评价值

表2　第2年评价值

表3　第3年评价值

取衰减系数λ=0.5，利用式(16)计算时间权重w=(0.186 3,0.307 2，0.506 5)。根据式(20)将近三年的区间三角模糊软集集成为综合区间三角模糊软集，计算结果如表4所示。

表4　综合区间三角模糊软集

利用式(22)计算各企业的选择值为

μ1=[(1.531,1.834);2.008;(2.183,2.491)]

μ2=[(1.299,1.611);1.675;(1.760,2.214)]

μ3=[(1.956,2.264);2.386;(2.461,2.848)]

μ4=[(1.400,1.704);1.825;(1.998,2.487)]

利用式(23)计算各企业的决策值为

η1=0.254，η2=-5.699

η3=7.725，η4=-2.280

由于η3值最大，因此运载火箭技术研究院选择企业x3进行长期合作。

5结论

本文提出了区间三角模糊软集的概念以及软子集、“AND”、“OR”、补等定义，探讨了相关运算性质并给出证明，进一步丰富了模糊软集理论。同时，建立基于区间三角模糊软集的动态决策模型，由于考虑了时间变化的影响使得决策过程更加符合实际，通过集成运算使得决策结果更为可靠。最后实例分析表明，所提出的方法有效，且易于编程计算。

参考文献：

[1] Miao B Q, Hu T Z.Probabilitytheory[M].Hefei:Press of University of Science and Technology of China,2009:1-15.(缪柏其,胡太忠.概率论教程[M].合肥:中国科学技术大学出版社,2009:1-15.)

[2] Gorzalczany M B. A method of inference in approximate rea-soning based on interval-valued fuzzy sets[J].FuzzySetsandSystems,1987,21(1):1-17.

[3] Zadeh L A.Fuzzy sets[J].InformationandControl,1965,8(3):338-353.

[4] Pawlak Z. Rough sets[J].InternationalJournalofComputerandInformationSciences, 1982, 11: 341-356.

[5] Molodtsov D. Soft set theory-first results[J].ComputersandMathematicswithApplications, 1999, 37(4):19-31.

[6] Maji P K, Biswas R, Roy A R. Fuzzy soft sets[J].JournalofFuzzyMathematics, 2001, 9(3): 589-602.

[7] Maji P K, Biswas R, Roy A R. Intuitionistic fuzzy soft sets[J].JournalofFuzzyMathematics, 2001, 9(3): 677-692.

[8] Yang X B, Lin T Y, Yang J Y, et al. Combination of interval-valued fuzzy set and soft set[J].ComputersandMathematicswithApplications, 2009, 58(3): 521-527.

[9] Jiang Y C, Tang Y, Chen Q M, et a1. Interval-valued intui-tionistic fuzzy soft sets and their properties[J].ComputersandMathematicswithApplications,2010,60(3):906-918.

[10] Ali M I. A note on soft sets, rough soft sets and fuzzy soft sets[J].AppliedSoftComputing,2011,11(4):3329-3332.

[11] Maji P K, Roy A R, Biswas R. An application of soft sets in a decision making problem[J].ComputersandMathematicswithApplications, 2002, 44(8):1077-1083.

[12] Roy A R, Maji P K. A fuzzy soft set theoretic approach to decision making problems[J].JournalofComputationalandAppliedMathematics, 2007, 203(2): 412-418.

[13] Kong Z, Gao L Q, Wang L F. Comment on "A fuzzy soft set theoretic approach to decision making problems"[J].JournalofComputationalandAppliedMathematics, 2009, 223(2): 540-542.

[16] Feng F, Jun Y B, Liu X, et al. An adjustable approach to fuzzy soft set based decision making[J].JournalofComputationalandAppliedMathematics, 2010, 234(1): 10-20.

[17] Jiang Y C, Tang Y, Chen Q M. An adjustable approach to intuitionistic fuzzy soft sets based decision making[J].AppliedMathematicalModeling, 2011, 35(2): 824-836.

[18] Kuang T L, Xiao Z. A multi-criteria decision making approach based on triangle-valued fuzzy soft sets[J].JournalofConvergenceInformationTechnology, 2012, 7(15): 17-25.

[19] Kuang T L. Trapezoid-valued fuzzy soft sets and its applications[J].AdvancesinInformationSciencesandServiceSciences, 2012, 4(15): 310-316.

[20] Mao J J, Yao D B, Wang C C, et al. Group decision-making method based on time-series fuzzy soft sets[J].SystemsEngineeringTheory&Practice,2014,34(1):182-189.(毛军军,姚登宝,王翠翠,等.基于时序模糊软集的群决策方法[J].系统工程理论与实践,2014,34(1):182-189.)

[21] Xu Z S. Intuitionistic fuzzy aggregation operators[J].IEEETrans.onFuzzySystems, 2007, 15(6): 1179-1187.

[22] Zhang S F, Liu S Y, Zhai R H. An extended GRA method for MCDM with interval-valued triangular fuzzy assessments and unknown weights[J].Computers&IndustrialEngineering, 2011, 61(4): 1336-1341.

陈孝国(1978-)，男，博士研究生，主要研究方向为模糊分析及决策。

E-mail：kjdxcxg@sohu.com

杜红(1972-)，女，教授，博士，主要研究方向为模糊决策及预测。

E-mail：longjiangchenguo@eyou.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141019.2344.005.html

Interval-valued triangular fuzzy soft set and its method

of dynamic decision making

CHEN Xiao-guo1,2， DU Hong2

(1.SchoolofMechanicsandCivilEngineering,ChinaUniversityofMining&Technology,Beijing100083,

China; 2.SchoolofScience,HeilongjiangUniversityofScienceandTechnology,Harbin150022,China)

Abstract:The concept of interval-valued triangular fuzzy soft set is presented and the relative operations and properties are discussed for improving the fuzzy soft theory. A dynamic decision making model is established based on the definition of interval-valued triangular fuzzy soft set, in which the determination of period weights is by the use of exponential decay method, and the arithmetic weighted average operator of interval-valued triangular fuzzy soft set has been given by the aggregating thought, thereby aggregating different time-series interval-valued triangular fuzzy soft sets into a collective interval-valued triangular fuzzy soft set. The formulas of different objects selection and decision-making value have been given, therefore the optimal decision-making is achieved according to the size of the decision values. Finally, the steps of the proposed method have been concluded, and some examples are given to explain the application of the method.

Keywords:interval-valued triangular fuzzy soft set; aggregating; dynamic decision making; fuzzy soft matrix

作者简介：

中图分类号：C 934

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.21

基金项目：国家自然科学基金(51105135)；黑龙江省自然科学基金(A201015)资助课题

收稿日期：2014-05-19；修回日期：2014-06-30；网络优先出版日期：2014-10-19。