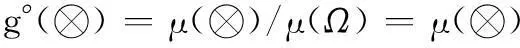基于Choquet积分的区间灰数多属性决策方法

王　霞， 党耀国

(南京航空航天大学经济与管理学院， 江苏 南京 211106)



基于Choquet积分的区间灰数多属性决策方法

王霞， 党耀国

(南京航空航天大学经济与管理学院， 江苏 南京 211106)

摘要：针对多属性决策中属性间的关联性对决策结果的影响，提出了基于区间灰数灰度和Choquet积分的区间灰数多属性决策方法。根据区间灰数灰度的定义，证明了区间灰数的灰度是一种灰测度，由此定义了关于区间灰数灰度的离散Choquet积分并证明其性质；依据各方案的综合属性值的方差最小的原则建立多目标优化模型，确定了各属性或属性集的权重，最后利用Choquet积分对各方案的效果评价向量进行集成。通过实例说明了该方法的有效性。

关键词：区间灰数； 关联性； 灰度； Choquet积分

0引言

多属性决策[1]是研究不确定性决策问题的一种系统分析方法,其目的是改进决策过程，从一系列备选方案中找出满足一定目标的最优方案。决策属性指标体系的构建是影响决策结果合理性的重点问题之一，因此所建立的决策属性指标体系应满足代表性、完备性和独立性,但在实际应用中独立性往往难以达到，故在多数情况下决策者会忽略属性指标体系间的独立性[2]。属性之间的关联性，使得属性权重的可加性遭到破坏，导致加权求和后得到与实际不相符的结论。文献[3]指出了现实决策问题中常存在关联，这是决策分析从理论迈向应用的瓶颈，并介绍了基于关联的多属性决策分析理论的发展情况，分析其研究特点和热点；文献[4]对属性间的关联性进行了总结,并分析其对决策结果的影响。由此可见，在多属性决策中对属性间具有关联性的问题进行研究，具有重要的理论和现实意义。文献[5]利用加权马氏距离对传统的灰靶决策方法进行改进,避免了决策指标间的相关性、不同量纲和重要性差异对决策效果的影响以及灰靶变换的不相容问题；文献[6]定义了广义三角模糊相关平均算子，该算子不仅考虑了元素间的重要性而且反映了元素间的相关性，并把该算子应用到多属性决策中；文献[7]针对多属性群决策中专家权重和属性权重通常具有相关性的问题，提出了两类诱导直觉模糊相关集成算子；文献[8]定义了诱导Choquet积分算子，并利用该算子研究了决策者对方案有模糊偏好且偏好间存在相互关联的群决策问题。文献[9]提出Choquet容度及其积分，Choquet积分考虑了属性间存在相互影响的情况，即属性间的互补性或可替代性可以由容量模拟。文献[10]首次把Choquet积分理论应用到决策理论中，目前Choquet积分已经被广泛应用到数据源选择、经济效益研究、绩效评价等多个领域。

在现实管理决策问题中，由于实际问题的多样性和不确定性以及人类认识的局限性，决策者在决策过程中往往难以给出确切的属性值，区间灰数[11]作为处理多属性不确定性决策问题的一种手段，自提出以来一直是研究的热点。文献[12]提出了基于信息还原算子的区间灰数序列关联度的计算方法，建立了多指标区间灰数关联决策模型；文献[13]推导了信息分布已知条件下区间灰数“核”的计算公式，在此基础上通过比较各指标值与靶心连线所围成图形的面积大小来对方案的优劣进行评价。

综上所述，对于属性值是区间灰数且属性间具有关联性的多属性决策问题，在目前的研究基础上，本文将Choquet积分应用于属性值是区间灰数的多属性决策中，提出了基于区间灰数灰度和Choquet积分的区间灰数多属性决策方法，通过实例说明了该方法的合理性和有效性。

1基本知识

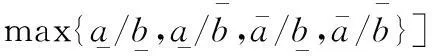
为区间灰数a(⊗)≥b(⊗)的可能度。

定义 3[11]设灰数⊗产生的背景或论域为Ω，μ(⊗)为灰数⊗取数域的测度，则称

为灰数⊗的灰度。

(1) 若⊗1⊂⊗2，则g°(⊗1)≤g°(⊗2)

(2) 若⊗1∩⊗2=φ，则

若⊗1∩⊗2≠φ，则

证明(1) 由灰度的定义知，当⊗1⊂⊗2时，易证

g°(⊗1)≤g°(⊗2)

(2) 若⊗1∩⊗2=φ，

若⊗1∩⊗2≠φ，

证毕

由定理1可知，区间灰数的灰度满足单调性和次可加性，因此可认为区间灰数的灰度为一种灰测度。

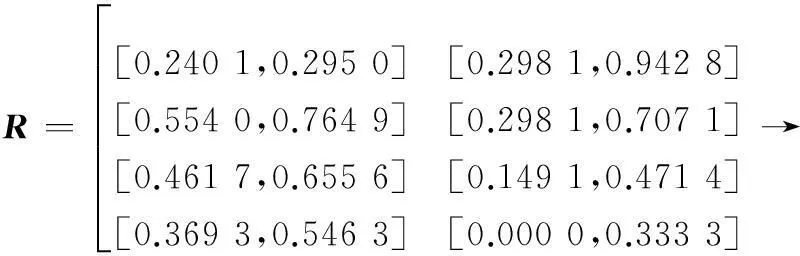
设任一多属性决策问题的属性集为X，对于任意的T⊆X，g°(T)可认为是属性集的权重或者是重要程度。∀S,T⊆X，若g°(T∪S)=g°(T)+g°(S)，则表明属性集间相互独立；g°(T∪S)

Choquet容量是一种非可加测度,Choquet积分是关于非可加测度的一种非线性积分，Choquet容量和Choquet积分是概率测度和数学期望的自然推广，是在非可加测度下研究问题。

定义 4[12]设X是非空集合，P(X)是X的幂集，u是定义在P(X)上的集函数u:P(X)→[0,1]，若u满足以下两个条件：

(1) u(X)=0，u(X)=1；

(2) ∀S,T⊆X，S⊆T，则u(S)≤u(T)则称u是定义在P(X)上的容量。

定义 5[12]设X={x1,x2,…,xn}为非空集合，P(X)是X的幂集，f为定义在X上的非负函数，u为定义在P(X)上的容量，则f关于容量u的离散Choquet积分为

式中，为f(x(i))向量的变换，使得

0≤f(x(1))≤f(x(2))≤…≤f(x(n))，A(i)={xi, xi+1,…,xn}且A(n+1)=0。

由上所述，根据灰度的性质和Choquet积分的定义，可以定义区间灰数关于灰度的离散Choquet积分。

定义 6设X={x1,x2,…,xn}为一区间灰数序列，P(X)是X的幂集，f为定义在X上的非负函数，g°(⊗)为区间灰数的灰度，则f关于灰度g°(⊗)的离散Choquet积分为

式中，(i)为f(x(i))向量的变换，使得

0≤f(x(1))≤f(x(2))≤…≤f(x(n))，A(i)={xi, xi+1,…, xn}且A(n+1)=0。

由定义6以及定理1可知，关于灰度g°(⊗)的离散Choquet积分作为一种合并算法，考虑了属性间存在冗余关联的情况，即属性间的关联可以由灰度g°(⊗)来模拟。

由区间灰数的运算法则和关于灰度g°(⊗)的离散Choquet积分，可以得到区间灰数离散Choquet积分的如下性质：

性质 1(幂等性)设ai(⊗)(i=1,2,…,n)为一组区间灰数，g°(⊗)为区间灰数的灰度，若

则

证毕

又由ai(⊗)≥bi(⊗)得

即λiai(⊗)≥λibi(⊗)，故

证毕

则有

则有

于是有

即证C(a1(⊗),a2(⊗),…,an(⊗))≥a-(⊗)。

同理可证C(a1(⊗),a2(⊗),…,an(⊗))≤ a+(⊗)。故a-(⊗)≤C(a1(⊗),a2(⊗),…,an(⊗))≤a+(⊗)

证毕

2基于Choquet积分的区间灰数多属性决策方法

醇类化合物主要由甲基酮和醛类的还原、氨基酸的降解及脂肪分解氧化产生，直链醇可以通过脂质氧化生成，而支链醇由 Strecker降解产生的支链醛还原得到[25,26]，直链低级醇一般无风味，但随碳链的增加而产生芳香和脂肪香等香味。低气味阈值的醇是板鸭制品香味的贡献者，具有令人愉快的水果味和花香味[27]。各地区板鸭的醇类含量比例均较高，醇类属普遍性挥发性风味物质，其中南京板鸭的醇类含量最高，种类最多，与徐为民等[16]的研究一致。1-戊醇带有面包香、酒香和果香，只在沙县竹炭板鸭和雷官板鸭中检测；苯乙醇只存在于南京板鸭中，具有玫瑰香，广泛应用于酿酒工业、化妆品和香料中。

对某一多属性决策问题的属性集X={x1,x2,…,xm}，可以把属性集X={x1,x2,…,xm}看作是属性集产生的背景或论域Ω，因此把属性集X可作一个整体，即可以取μ(Ω)=1，则由区间灰数灰度的定义可知

对于⊗={xi1,xi2,…,xip}⊂Ω，其中p≤m，则μ(⊗)可以认为是专家给出的选取属{xi1,xi2,…,xip}的重要程度。

由上述所述，则各方案的综合评价值为

(1)

C(hi)仍为一区间灰数。

(2)

求解上述模型可得属性集的测度μ(Ai)。利用式(1)得到各方案综合属性值，再用区间灰数的可能度，对各方案的综合评价值进行大小排序。

3实例分析

本文以文献[15]中的案例为例进行分析。某部队在采购火炮武器时，有4种系列的火炮hi(i=1,2,3,4)可供选择，并考虑下例5项属性：x1为火力突击能力系数；x2为反应能力指数；x3为机动能力指数；x4为生存能力指数；x5为成本(元)，各方案关于评价属性的效果值如表1所示。

表1　决策矩阵

在本例中除了成本外，其余均为效益型属性，利用文献[15]中的规范化方法，得到规范化矩阵为

本文利用区间灰数的可能度，对方案hi的一致效果评价向量的各分量重新进行排序，得到排序后各方案的新的一致效果评价向量。把属性集看作一个整体，即有μ(Ω)=1，则得到

故μ(⊗)可以认为是属性{xi1,xi2,…,xip}的权重，利用Lingo11求解式(2)得到属性集的权重如表2所示。

根据式(1)对各方案的效果向量进行信息集成，得到各方案的综合评价值为

C(h1)=[0.401 4,0,478 1]

C(h2)=[0.369 9,0.443 9]

C(h3)=[0.388 4,0.478 7]

C(h4)=[0.338 6,0.539 4]

再利用区间灰数的可能度，对各方案的综合评价值进行大小排序

则方案的优劣顺序为h1fh4fh3fh2，故决策者可优先考虑h1。

表2　属性集的灰测度μ

文献[15]中方案的排序为h1fh3fh2fh4，可看出该排序与本文排序不完全一致，主要差别是h3和h4的排序位置不同。主要原因是文献[15]中的方法没有考虑属性间的关联性，直观来看各属性间不具有独立性，即各属性间存在关联性；从数据直观来看，方案h3和h4在属性x1、x2、x4下的属性值差别不大，在属性x3、x5下的属性值相差很大，从属性极性来看，在属性x3、x5下方案h4的值较方案h3更符合决策者的理想值。

从以上分析可以看出，属性间的关联性会对决策的结果产生影响，在实际决策中由于问题的复杂性，属性间常存在相互关联，若假设属性间是相互独立的，则会影响决策结果的合理性, 因此在决策中考虑属性间具有关联的情况有一定的实际意义。

4结论

在多属性决策中，决策属性指标体系的构建是影响决策结果合理性的重点问题之一，本文针对多属性决策中属性间的关联性对决策结果的影响，提出了基于区间灰数灰度和Choquet积分的区间灰数多属性决策方法。首先由区间灰数灰度的定义，证明了区间灰数灰度的非可加性，即证明区间灰数的灰度是一种灰测度，进而定义了区间灰数的离散Choquet积分，并证明其性质；最后利用区间灰数的离散Choquet积分集成方案的综合属性值，并通过实例说明了该方法的有效性和合理性。

参考文献：

[1]XuZS. Uncertain multiple attribute decision making methods and application[M].Beijing:TsinghuaUniversityPress,2004.(徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.)

[2]BiKX,SunJH,ZhangTZ,etal.Measurementandevaluationofregionaltechnologicalinnovationinsmallandmediumenterprisesbasedonfuzzyintegral[J].Systems Engineering-Theory & Practice,2005,25(2):40-46.(毕克新,孙金花,张铁柱,等.基于模糊积分的区域中小企业技术创新测度与评价[J].系统工程理论与实践,2005,25(2):40-46.)

[3]ZhangL,ZhouDQ.Basedonthecorrelationanalysisofmultipleattributedecisionmakingtheoryresearchreviewed[J].Management Review,2008,20(5):51-57.(章玲,周德群.基于关联的多属性决策分析理论研究综述[J].管理评论,2008,20(5):51-57.)

[4]MarichalJL.AnaxiomaticapproachofthediscreteChoquetintegralasatooltoaggregateinteractingcriteria[J].IEEE Trans.on Fuzzy Systems,2000,8(6):800-807.

[5]WangZX,DangYG,YangH.Improvementsondecisionmethodofgreytarget[J].Systems Engineering and Electronics, 2009, 31(10): 2634-2635. (王正新, 党耀国, 杨虎. 改进的多目标灰靶决策方法[J]. 系统工程与电子技术, 2009, 31(10):2634-2635.)

[6]WeiGW,ZhaoXF,LinR,etal.Generalizedtriangularfuzzycorrelatedaveragingoperatorandtheirapplicationtomultipleattributedecisionmaking[J].Applied Mathematical Modelling,2012,36(7):2975-2982.

[7]WeiGW,ZhaoXF.Someinducedcorrelatedaggregatingoperatorswithintuitionisticfuzzyinformationandtheirapplicationtomultipleattributegroupdecisionmaking[J].Expert Systems with Applications,2012,39(2):2026-2034.

[8]TanCQ,MaBJ，ChenXH.GroupdecisionmakingmethodbasedoninducedChoquetintegraloperator[J]. Journal of Industrial Engineering and Engineering Management,2010,24(4):155-160.

[9]ChoquetG.Theoryofcapacities[J]. Annales de l′institut-Fouri,1953,5:131-295.

[10] Schmeidler D. Subjective probability and expected utility without additivity[J].Econometric, 1989,57(3):571-587.

[11] Liu S F, Dang Y G, Fang Z G, et al.Greysystemtheoryanditsapplication[M].Beijing:Science Press,2010.(刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.)

[12] Yang B H, Fang Z G, Zhou W, et al. Incidence decision model of multi-attribute interval grey number based on information reduction operator[J].ControlandDecision,2012,27(2):182-186.(杨保华,方志耕,周伟,等.基于信息还原算子的多指标区间灰数关联决策模型[J].控制与决策,2012,27(2):182-186.)

[13] Zeng B, Liu S F，Li C, et al. Grey target decision-making model of interval grey number based on cobweb area[J].SystemsEngineeringandElectronics,2013,35(11):2329-2334.(曾波,刘思峰,李川,等.基于蛛网面积的区间灰数灰靶决策模型[J].系统工程与电子技术,2013,35(11):2329-2334.)

[14] Xu Z S, Da Q L. Possibility degree method for ranking interval numbers and its application[J].JournalofSystemsEngine-ering,2003,18(1):67-70.(徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70.)

[15] Song J, Dang Y G, Wang Z X, et al. New decision model of grey target with both the positive clout and the negative clout[J].SystemsEngineering-Theory&Practice,2010,30(10):1822-1827.(宋捷,党耀国,王正新,等.正负靶心灰靶决策模型[J].系统工程理论与实践,2010,30(10):1822-1827.)

王霞(1985-)，女，博士研究生，主要研究方向为灰色系统理论与决策分析。

E-mail：wangxia0509@163.com

党耀国(1964-)，男，教授，博士研究生导师，主要研究方向为灰色系统理论、数量经济。

E-mail：iamdangyg@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141030.1136.013.html

Approach for multiple attribute decision-making with interval grey

number based on Choquet integral

WANG Xia， DANG Yao-guo

(CollegeofEconomicsandManagement,NanjingUniversityofAeronauticsand

Astronautics,Nanjing211106,China)

Abstract:With regard to the interaction between attributes which has influenced on decision results in multiple attribute decision making, a multiple attribute decision making method of interval grey number based on degree of greyness and Choquet integral is presented. Degree of greyness of interval grey number is proved as a grey measure according to its definition, then discrete Choquet integral of degree of greyness of interval grey number is defined, and some of its properties are investigated. The weight of each attribute or attribute set is determined by using a multi-objective optimization model，which variance of comprehensive attribute values of each scheme is minimum; and the effect evaluation vector of each scheme are integrated based on Choquet integral. Finally, an example is also presented to illustrate the effectiveness of the proposed method.

Keywords:interval grey number; interaction; degree of greyness; Choquet integral

作者简介：

中图分类号：N 941.5

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.20

基金项目：国家自然科学基金(71071077，71371098)；中央高校基本科研业务费专项资金(NC2012001)；江苏省高校哲学社会科学重点研究基地重大项目(2012JDXM005)；江苏省普通高校研究生科研创新计划(CXZZ130183)资助课题

收稿日期：2014-06-24；修回日期：2014-09-18；网络优先出版日期：2014-10-30。