连续时空最优搜索者路径问题的改进双链遗传算法

张　献, 任耀峰, 沈　静

(海军工程大学理学院, 湖北 武汉 430033)



连续时空最优搜索者路径问题的改进双链遗传算法

张献, 任耀峰, 沈静

(海军工程大学理学院, 湖北 武汉 430033)

摘要：针对连续时空马尔可夫运动目标的最优搜索者路径问题(optimal searcher path problem,OSPP),建立了搜索者方向和速度均作为决策变量的搜索路径规划模型,给出了一种改进的双链遗传算法(improved double chains genetic algorithm,IDCGA)。算法采用双链实数编码策略表达搜索路径,利用混沌初始化方法产生初始种群,提出了变异幅度自适应控制的方法,通过引入基因位自适应因子η和进化代数自适应因子λ对变异操作进行了改进。以反潜搜索问题为例进行的仿真实验表明,所提出的算法具有稳定性好、寻优能力强、收敛速度快等优点,适用于求解复杂搜索路径问题。

关键词：最优搜索者路径; 连续时空; 马尔可夫目标; 双链遗传算法; 自适应变异

0引言

搜索论是主要研究利用探测手段寻找指定目标优化方案的理论和方法,起源于二战时期美国反潜运筹小组对德国潜艇进行搜索的一系列研究工作。1956～1980年,在众多学者的努力下[1-3],取得了一批主要针对静止目标和运动目标最优搜索资源分配问题的理论成果,奠定了搜索论的理论基础。无论在离散时空还是连续时空,此类问题都要求搜索资源能够任意细分,同时搜索者的运动能力不受约束,可在搜索空间内任意转移并分配搜索资源。

OSPP是搜索论中搜索者运动受到约束的一类复杂优化问题,要求搜索者在有限资源约束下,构造一个搜索路径使得搜索效益最大。1986年,Trummel已经证明OSPP是一个NP完备性问题[4]。许多学者采用分支定界法[5-7]、割平面法[8]、启发式算法[9-10]、贪婪算法[11]等方法进行了研究。这些方法都需要进行离散化,先将搜索空间分割成许多单元格,目标被限制在单元格中,大多被假定为静止或作离散状态的Markov运动,搜索者在单元格中进行搜索,探测仅作用于搜索者所处的单元格内。由于问题的复杂性,算法的设计常在优化效果与计算时间上折中。目前，尚未找到一种具有一般性的有效算法来解决该问题[12]。

为使模型更贴近实际,部分文献讨论了更为复杂的连续时空OSPP。其中文献[13-14]利用了最优控制理论,但要求目标和搜索者的运动满足严格的微分方程。文献[15]首次将遗传算法(genetic algorithm,GA)应用于连续时空OSPP,所得效果令人鼓舞,体现出GA求解复杂路径规划的优势。文献[16]提出一种对搜索者方向编码的高变异率GA,讨论了静止目标和简单定向运动目标的搜索问题,算例结果表明该算法相比文献[15]的算法对求解OSPP的效果有明显提高。

本文研究目标运动为时空连续马尔可夫过程的OSPP,使问题更为一般化。首先建立了目标和搜索者的运动模型,将搜索者方向和速度均作为决策变量,提出变异幅度自适应控制的方法,给出了IDCGA。最后将算法应用于两个仿真例子,通过算法对比验证了IDCGA的有效性。改进的算法具有稳定性好、寻优能力强等优点,适用于求解复杂搜索路径问题。研究成果对求解OSPP具有一定应用价值。

1连续Markov运动目标模型

连续时空下,文献[15-16]讨论了静止目标和简单定向运动目标的OSPP,本文考虑更为复杂的马尔可夫运动目标。假定目标位置是一个状态空间为R2,时间集为[0,+∞)的二维马尔可夫过程{X(t),t≥0},即目标的位置具有无后效性:如果已知目标现在时刻t′所处的状态,则目标将来时刻t(t>t′)所处位置的概率分布只与目标现在所处的位置有关,而与目标过去的位置无关。对于一般马尔可夫运动目标的转移概率分布函数F(X,t|X′,t′)的解析表达式不易求出,可通过蒙特卡罗方法及概率统计近似计算。

本文讨论的搜索问题属搜索论中的单向搜索范畴,即目标不能对搜索者的行为做出反应,其运动不受搜索者策略影响。同时，不考虑深度,搜索者和目标在2维空间内运动。

2搜索路径的表达

实际问题中,目标和搜索者通常在一定时间段内保持稳定的运动方向和速度,每隔一段时间根据情况进行调整(如舰船和潜艇)。

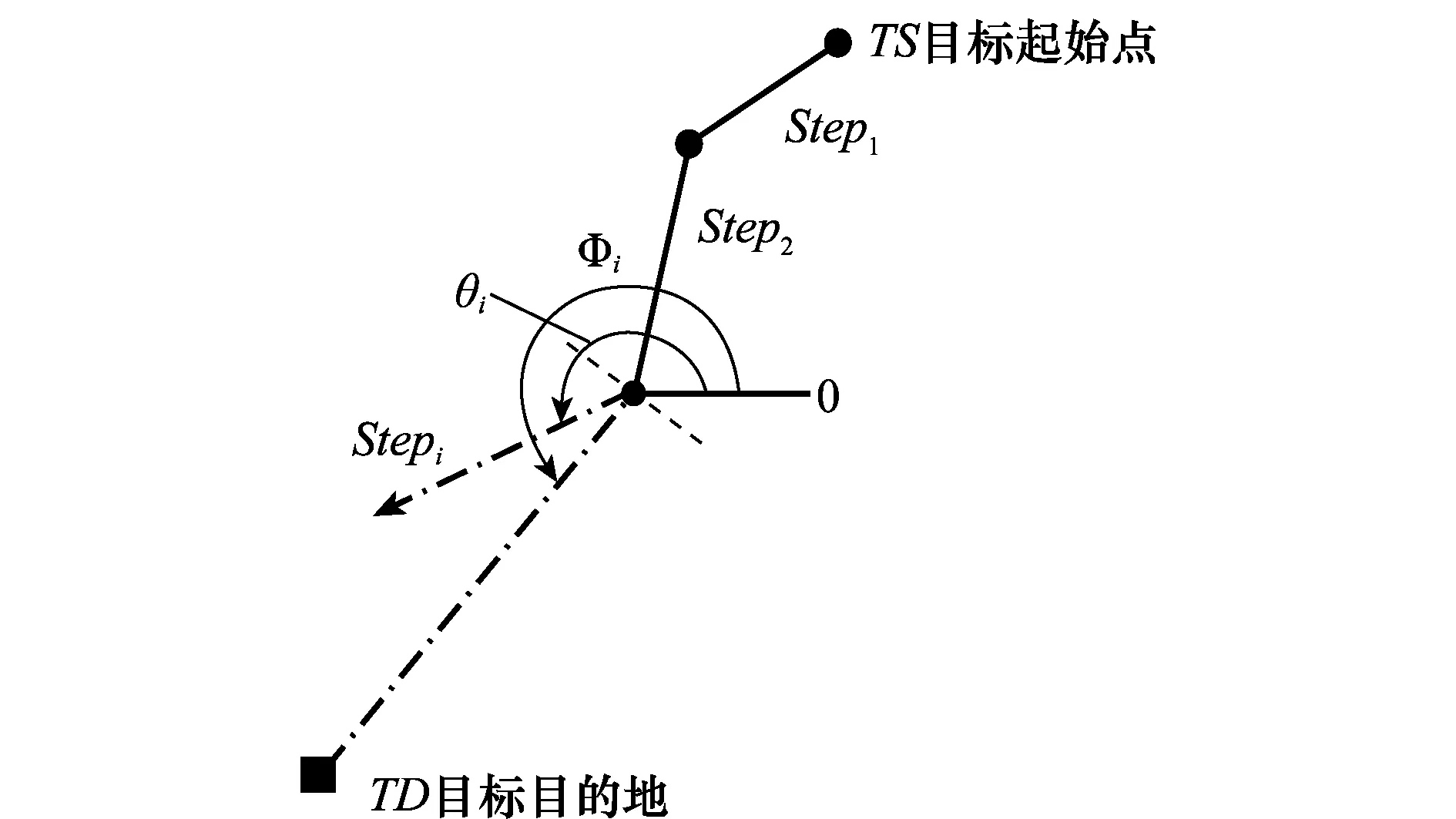
现把方向、速度稳定不变的运动过程视为一个阶段(Step)。利用搜索者起始坐标SS、搜索时间Tsearch、阶段时长SteptS、各阶段方向θS和速度VS共5个要素表达搜索路径(下标S表示搜索者),其中θS∈[0,2π),VS∈[Vmin,Vmax]。文献[16]固定SteptS和VS,将θS视为变量。本文进一步深入,将方向θS和速度VS同时作为决策变量(见图1和图2),使模型更一般化。

图1　方向的表达

图2　搜索路径的表达

3OSPP的规划模型描述

3.1目标函数

利用累积探测概率(cumulativedetectionprobability,CDP)作为搜索路径规划的目标函数,用于评价路径的搜索效率。在0≤t≤T时,t时刻的CDP记为FCDP(t),定义为时间段[0,T]内至少一次探测到目标的概率:

FCDP(t)=P{在时刻 t 以前至少一次探测到目标}=

P{初次探测到目标的时间≤t }

对一般搜索路径,通过解析方法求得精确的FCDP是很困难的,可采用蒙特卡罗方法近似计算[15-16]。本文在仿真中讨论搜索者利用声纳搜索水下目标的问题,其中声纳的探测方程为理想模型,即当目标位于声纳作用距离(Lsonar)内探测到目标的概率为1,否则为0。

3.2规划模型

OSPP的规划模型描述为

maxFCDP(X,t)

(1)

式中,决策变量X=(x1,x2,…,x2N)T表示一种搜索路径规划方案,N表示搜索路径阶段总数,(x1,x2,…,xN)T表示搜索路径各阶段的方向θS;(xN+1,xN+2,…,x2N)T表示各阶段的速度VS。约束条件φ={X|xi∈[ai,bi],ai

4IDCGA

文献[15-16]将GA应用于连续时空OSPP,并取得不错的效果。本文提出一种IDCGA求解OSPP。IDCGA采用双链基因实数编码策略、混沌初始种群策略以及保留、交叉、变异3种遗传操作。针对OSPP特点,提出变异幅度自适应控制的方法,并通过引入2种自适应因子改进了变异操作。

4.1双链基因实数编码策略

4.2混沌初始种群策略

为使初始种群具有较好的多样性,利用混沌现象的随机性、不重复遍历等特性,IDCGA采用Logistic映射的混沌初始化方法。

随机生成2N个实数y1i(y1i∈(0,1), y1i≠0.5,i=1,2,…,2N),并作为Logistic映射的初始值。通过式(2)得到第j个混沌序列{yj1,yj2,…,yj2N}。

(2)

式中,j=2,3,…,M。由式(3)进行解空间变换,得到M组决策变量X。

(3)

4.3改进的遗传操作

IDCGA的遗传操作包括保留、交叉、变异3种独立的遗传算子,算法流程图见图3。在遗传操作方面,IDCGA与普通GA相比,主要不同点有:一是采用提出的自适应变异策略;二是双链染色体同基因位的基因θi,Vi一同进行遗传操作;三是3种遗传算子独立运算,得到的3组新个体组成子代种群;四是分别将3组新个体占子代的比例记为保留概率PS、交叉概率PC、变异概率PM(PS+PC+PM=1)。

图3　IDCGA流程图

4.3.1保留

将父代一组精英个体直接保留到子代,此操作也称为稳态选择[17],其中选取的个体数为PS×M。

4.3.2交叉

采用轮盘赌法从父代中选取一组个体,并两两进行单点交叉[17],产生的新个体遗传到子代。其中交叉点在染色体长度的1/4至3/4处随机选择,选取交叉操作的个体数为PC×M。

4.3.3变异及改进

变异操作中,基因的变更通常通过简单地产生随机数代替父代基因。针对OSPP特点,本文采用较高的变异概率保证种群的多样性,避免早熟收敛。为使变异更高效,提出变异幅度自适应控制的方法。现考虑以下两个方面的问题:

(1) 不同阶段搜索者的方向和速度对搜索路径的灵敏性。在图4中,将路径1分别对不同阶段的方向作幅度相同的变异操作得到路径2和路径3。可以看出,阶段越是靠前的方向变化对路径的改变越是剧烈,因此阶段越靠前的方向对搜索路径的灵敏性越大。在OSPP中,搜索的前期阶段选择正确的搜索方向尤为关键。将路径3的第1阶段速度作幅度相同的变异操作得到路径4。分析可得,速度相对于方向对搜索路径的灵敏性较小。变量的次序及类别影响变量的灵敏性,这是OSPP与其他数值优化问题的一个关键区别。因此变异幅度应根据变量的次序及类别自适应调整,特别是针对较优个体的变异。

图4　搜索者方向和速度对搜索路径的灵敏性分析

(2) 不同进化阶段变异幅度对进化的影响。在进化前期变异有助于增加种群的多样性。在进化后期,优秀个体接近最优解,应该避免剧烈变异。如果变异剧烈(例如方向的180°旋转),将使变异效率低,甚至牵制进化。为了使变异更高效,变异幅度应随进化代数的增加自适应减小。

文献[16]的变异方法只作用于父代最优个体,本文对保留操作中的精英个体组进行变异操作,其中随机选取的个体数为PM×M。为提高变异效率、加快算法收敛,本文还提出了自适应变异策略:

(4)

(5)

若变异后基因值超出可行解空间φ,通过式(6)调整:

(6)

在式(4)中,变异幅度由C、Rand、λ和η共同控制。如果不引入自适应因子λ和η,变异幅度仅由C、Rand控制,式(4)的变异与普通变异没有本质区别。

引入基因位自适应因子η后,变异幅度随基因位次序线性递增,即在搜索路径中阶段越靠前的方向变异幅度越小,使得对精英个体的变异不易出现无效甚至离谱的反差,保证了变异的高效性。因为速度相比方向对路径的灵敏性小,未对V基因引入η因子。

引入进化代数自适应因子λ后,算法在进化前期变异幅度大,可以广泛搜索解空间,避免早熟收敛。进化后期变异幅度自适应减小,通过对精英个体的微调,提高变异效率。因此λ起到由“求泛”到“求精”的自适应搜索作用。

IDCGA通过自适应控制逐步寻优,保证了多样性和高效性,实现了全局搜索和局部搜索的动态平衡,使算法收敛速度快、优化结果稳定。

5仿真与分析

在实际中,OSPP的应用领域十分广泛,例如机器人搜索路径规划[6]、无人机侦察[18]、反潜搜索[15-16,19]等方面。本文选择两个舰艇搜索潜艇目标的军事问题作为算例,并通过算法对比验证IDCGA的有效性。

5.1逃离目标搜索

5.1.1问题描述

假设在某海域Time=0时刻,我方兵力探测到敌潜艇目标在TS点出水,随后潜入水下。已知潜艇入水后逃离出水点,并前往TD点附近区域执行任务。我方舰艇迅速赶往敌情区域,并制定搜索策略展开搜索。文献[9-10]在离散时空下讨论了类似逃离目标的搜索问题。

(1) 目标的仿真

利用目标起始坐标TS、目标目的地坐标TD、速度VT、方向θT、阶段时长SteptT共5个要素描述Markov运动目标(下标T表示目标),并利用Monte Carlo方法对目标路径进行仿真。已知目标起始点坐标为TS=(130,150);目的地TD服从均值为μTDx=μTDy=30(n mile),标准差为σTDx=σTDy=20/3,相关系数为ρXY=0的二维正态分布(见图5)。

图5　目标目的地分布及Time=5时刻分布

图6　目标各阶段方向的确定

图7　最优搜索路径及逃离目标运动路径分布

(2) 搜索者的相关参数

搜索者展开搜索的时刻Time=1,起始位置坐标为SS=(160,130),搜索时间为Tsearch=6 h,各阶段时长为SteptS=0.5 h,则阶段总数为NStep=Tsearch/SteptS=12。各阶段方向θS∈[0,2π)和速度VS∈[10 kn,25 kn],则变量总数为24。声纳作用距离Lsonar=3n mile,探测间隔时间Δtsonar=0.1 h。CDP的计算公式为

式中,NumT表示目标仿真的总数;NDetect(t)表示已探测到的目标数。

5.1.2仿真结果与算法比较

(1) 仿真结果

经50次独立运算,IDCGA得到的“最优”路径的FCDP(6)=79.33%(见图7),可以看出搜索者先后经历了“接近”、“拦截”、“追逐”、“拦截”、“回溯”几个主要阶段。其中算法参数为:种群规模M=120,染色体长度N=NStep=12,最大遗传代数Gmax=100,保留概率PS=0.2,交叉概率PC=0.2,变异概率PM=0.6。

(2) 算法对比

标准GA[17]的参数设置:M=130,PC=0.8,PM=0.01。文献[16]提出的GA*的参数设置:M=128,PS=0.25,PC=0.125,PM=0.625。

将本文IDCGA与标准GA、GA*的运算结果列于表1。

表1　逃离目标搜索的算法对比(50次运算)

表1中,IDCGA种群数量最少但平均FCDP最高,且最优FCDP和最差FCDP相差最小,因此算法稳定性好、寻优能力强、收敛速度快。GA*相对优化结果次之,但算法不够稳定,容易早熟。标准GA在求解复杂OSPP上效果不理想。IDCGA相比标准GA、GA*,平均FCDP的相对增长幅度为53.7%和10.5%。

图8和图9分别展示了GA*和IDCGA 50次运算结果中最优的10条搜索路径。可以看出IDCGA的稳定性好,所得最优路径接近,可视为收敛。因此相比文献[16]的算法,IDCGA在求解复杂运动目标OSPP上效果更好。

图8　GA*的10条最优搜索路径(逃离目标)

图9　IDCGA的10条最优搜索路径(逃离目标)

5.2方向未知目标搜索

5.2.1问题描述

假设Time=0时刻敌潜艇在TS=(90,160)出水,随后潜入水下(与第5.1节相同的问题描述不作赘述)。对于目标方向未知的情形,需要根据目标的某些信息合理地给出目标方向的概率分布。在本文中,假设目标沿主航向Φ航行,Φ服从μΦ=3π/2,σΦ=π/10的正态分布,路径各阶段的方向θT服从μθT=Φ,σθT=π/8的正态分布。目标的时空分布见图10和图11。时刻Time=1.5搜索者展开搜索,起始点SS=(40,150),搜索时间Tsearch=8h,则变量总数为32。

图10　Time=3,Time=8时刻目标分布

5.2.2仿真结果与算法比较

50次独立运算,IDCGA得到的“最优”路径的FCDP(8)=51.27%(见图11),算法对比结果见表2。图12和图13展示了GA*和IDCGA50次运算结果中最优的10条搜索路径。

表2　方向未知目标搜索的算法对比(50次运算)

图11　最优搜索路径及方向未知目标运动路径分布

图12　GA*的10条最优搜索路径(方向未知目标)

图13　IDCGA的10条最优搜索路径(方向未知目标)

IDCGA相比标准GA、GA*,平均FCDP的相对增长幅度为42.7%和10.7%。分析可得IDCGA具有稳定性好、寻优能力强、收敛速度快等优点,适用于求解复杂OSPP。

在实际应用中,对一般的探测模型可以利用等效的探测距离进行处理,只要合理地给出目标概率分布,利用本文算法即可求得“最优”的搜索路径,为决策者提供可行的搜索策略。

6结论

IDCGA引入2种自适应因子,采用变异幅度自适应控制的方法改进了变异操作,具有稳定性好、寻优能力强、收敛速度快等优点,在舰艇搜索潜艇的仿真例子中优化效果理想,适用于求解复杂的连续时空马尔可夫运动目标OSPP,研究成果对相关搜索问题具有一定启发意义。进一步工作可以将改进的算法应用于多搜索者问题和3维空间OSPP。

参考文献：

[1] Koopman B O. The theory of search[J].OperationResearch, 1956, 4(3): 324-346.

[2] Stone L D.Theoryofoptimalsearch[M]. New York: Academic Press, 1975.

[3] Brown S S. Optimal search for moving target in discrete time and space[J].OperationsResearch, 1980, 28(6):1275-1289.

[4] Trummel K E, Weisinger J R. The complexity of the optimal searcher path problem[J].OperationsResearch, 1986, 34(2):324-327.

[5] Eagle J N, Yee J R. An optimal branch-and-bound procedure for the constrained path, moving target search problem[J].OperationsResearch, 1990, 38(1): 110-114.

[6] Lau H, Huang S, Dissanayake G. Discounted MEAN bound for the optimal searcher path problem with non-uniform travel times[J].EuropeanJournalofOperationalResearch,2008,190(2):383-397.

[7] Sato H, Royset J O. Path optimization for the resource-constrained searcher[J].NavalResearchLogistics,2010,57(5):422-440.

[8] Royset J O, Sato H. Route optimization for multiple searchers[J].NavalResearchLogistics, 2010, 57(8): 701-717.

[9] Hong S P, Cho S J, Park M J. A pseudo-polynomial heuristic for path-constrained discrete-time Markovian-target search[J].EuropeanJournalofOperationalResearch, 2009, 193(2): 351-364.

[10] Hong S P, Cho S J, Park M J, et al. Optimal search-relocation trade-off in Markovian-target searching[J].Computers&OperationsResearch, 2009, 36(6): 2097-2104.

[11] Chen P, Wu X F, Chen Y. Method of call-search for Markovian motion targets using UUV cooperation[J].SystemsEngineeringandElectronics, 2012, 34(8): 1630-1634. (陈盼, 吴晓锋, 陈云. UUV编队协同应召搜索马尔可夫运动目标的方法[J]. 系统工程与电子技术, 2012, 34(8): 1630-1634.)

[12] Zhu Q X.Optimalsearchtheoryindiscreteandcontinuousspaces[M]. Beijing: Science Press, 2005. (朱清新. 离散和连续空间中的最优搜索理论[M]. 北京: 科学出版社, 2005.)

[13] Ohsumi A. Optimal searching for a Markovian-target[J].NavalResearchLogistics, 1991, 38(4): 531-554.

[14] Zhu Q X, Qing L, Peng B. Optimal control model of search problem for randomly moving targets[J].ControlTheory&Applications, 2007, 24(5): 841-845. (朱清新, 卿利, 彭博. 随机运动目标搜索问题的最优控制模型[J]. 控制理论与应用, 2007, 24(5): 841-845.)

[15] Kierstead D P, DelBalzo D R. A genetic algorithm applied to planning search paths in complicated environments[J].MilitaryOperationsResearch, 2003, 8(2): 45-59.

[16] Cho J H, Kim J S, Lim J S, et al. Optimal acoustic search path planning for sonar system based on genetic algorithm[J].InternationalJournalofOffshoreandPolarEngineering, 2007, 17(3): 218-224.

[17] Li M Q, Kou J S, Lin D, et al.Thebasictheoryandapplicationsofgeneticalgorithm[M].Beijing: Science Press, 2002. (李敏强,寇纪淞,林丹,等.遗传算法的基本理论与应用[M].北京:科学出版社,2002.)

[18] Wu W C, Huang C Q, Song L, et al. Cooperative search and path planning of multi-unmanned air vehicles in uncertain environment[J].ActaArmamentarii, 2011, 32(11): 1337-1342. (吴文超, 黄长强, 宋磊, 等. 不确定环境下的多无人机协同搜索航路规划[J]. 兵工学报, 2011, 32(11): 1337-1342.)

[19] Chen P, Wu X F. Optimal extended position call-search method for UUVs’ formation[J].SystemsEngineeringandElectronics,2013,35(5):987-992. (陈盼,吴晓锋,陈云.UUV编队协同最优扩方应召搜索方法[J].系统工程与电子技术,2013,35(5):987-992.)

张献(1990-),男,硕士研究生,主要研究方向为军事系统建模与运筹决策。

E-mail:919453887@qq.com

任耀峰(1959-),男,教授,博士,主要研究方向为军事系统建模与运筹决策。

E-mail:renyaofeng@sina.com

沈静(1980-),女,讲师,博士,主要研究方向为约束满足问题模型及其相变现象研究。

E-mail:shendina@hotmail.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20140820.1731.003.html

Improved double chains genetic algorithm for optimal searcher path

problem in continuous time and space

ZHANG Xian, REN Yao-feng, SHEN Jing

(CollegeofScience,NavalUniversityofEngineering,Wuhan430033,China)

Abstract:An improved double chains genetic algorithm (IDCGA) for optimal searcher path problem (OSPP) with Markovian-target in continuous time and space is proposed,and both the searcher’s direction and speed are considered as decision variables in the programming model of the search path. The algorithm uses a double-chains real-coded strategy to express the search path, generating initial population by the chaotic initialization method. An adaptive control method for the extent of mutation is proposed to improve the mutation operation by using locus adaptive factor η and generation adaptive factor λ.In the simulations of the anti-submarine searches, the results indicate that the proposed algorithm has the advantages of better stability, more powerful optimizing ability,faster convergence speed, and it is well suitable for solving the complex search path problem.

Keywords:optimal searcher path problem (OSPP); continuous time and space; Markovian-target; double chains genetic algorithm; adaptive mutation

作者简介：

中图分类号：O 229

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.18

收稿日期：2014-04-01；修回日期：2014-06-11；网络优先出版日期：2014-08-20。