最优未来空域窗模型

卢发兴， 贾正荣， 吴　玲， 余戌曈

(海军工程大学电子工程学院指挥与控制系， 湖北 武汉 430033)



最优未来空域窗模型

卢发兴， 贾正荣， 吴玲， 余戌曈

(海军工程大学电子工程学院指挥与控制系， 湖北 武汉 430033)

摘要：未来空域窗射击体制是一种近年发展起来的高炮射击体制。以往对它的数学描述只考虑了一组射击误差，通过定量构造的方式，给出了一种可行的未来空域窗模型。在考虑了炮弹间的相关误差，以毁伤目标的概率为效能指标，推导出了最优未来空域窗的模型，并给出了未来空域窗可实现的毁伤目标概率上界。最后通过算例，分析了各参数变化对未来空域窗的影响。结果表明:给出的未来空域窗模型优于已有的模型。

关键词：火控系统; 射击理论; 未来空域窗; 毁伤概率

0引言

为了提高对机动目标的拦截概率,近年发展起来的一种近程防空反导火炮射击体制，即未来空域窗射击体制。它的实质就是，在目标预测迎弹面内以预测目标未来点为中心，朝多个瞄准点射击，形成一个炮弹散布区域，这个区域称之为未来空域窗。国内最早详细对未来空域窗进行数学描述的是文献[1]，后来所有对未来空域窗的相关研究[2-3]都是以其为基础进行的。这些文献中的未来空域窗模型[4-9]，忽略了炮弹间的相关误差，通过定量构造的方式，给出了一种未来空域窗模型，这个模型并不保证其是最优的未来空域窗。本文从另一个角度，在考虑炮弹间的相关误差的基础上，以毁伤目标的概率为效能指标，给出未来空域窗的最优参数及毁伤目标概率的上界，为实现未来空域窗射击体制提供理论基础。

1最优未来空域窗的区域特性

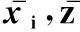
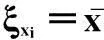
不妨设射击的不相关误差和相关误差服从正态分布，其归一化处理后的概率密度函数分别为f1(x1,z1)和f2(x,z)。

(1)

式中，ρ为正态常数，取ρ=0.476 936。

通过选择n个炮弹的瞄准点坐标，使之形成的未来空域窗毁伤目标概率Pn,ω最大，也就是目标未被毁伤的概率Pn,0最小，这样的未来空域窗是最优。由射击效能[10]可得

(2)

式中，p(x,z)为系统误差取x,z时，炮弹命中目标的概率。同样由射击效能，可得

(3)

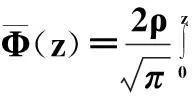
(4)

函数U(x,z)中包含有瞄准点相对坐标(ξxi,ξzi)，如果能够求解出使Pn,0最小的最优函数U(x,z)，通过最优函数U(x,z)可确定最佳的瞄准点相对坐标。为了求解最优函数U(x,z)，首先要对函数U(x,z)进行特性分析。显然由式(4)易知

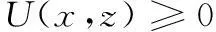
(5)

如果对U(x,z)进行积分，由(4)可知，可避免直接求解相对坐标(ξxi,ξzi)，由此可得

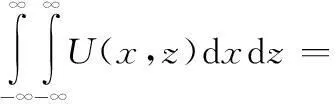
(6)

令

则有

(7)

把式(1)和式(4)代入式(2)可得

(8)

由指数函数特性和积分知识可知，式(8)中Pn,0最小等价于其被积分函数最小，设被积分函数为F(x,z)，F(x,z)为弹丸综合散布密度。

(9)

这样，求解未来空域窗的最优参数，转化为求解最优的U(x,z)函数，在满足式(5)和式(7)约束条件下，使得式(9)中的F(x,z)最小。由拉格朗日求极值法可得

(10)

式中，λ为拉格朗日系数，为0到1之间的常数。由约束条件式(7)可得

(11)

(12)

(13)

这样，最优未来空域窗的区域是一个椭圆，其半轴为Rx,Rz，表达式为

(14)

把式(12)代入Pn,0的被积分函数式(9)可得

(15)

由式(15)可看出，为了实现最优的未来空域窗，窗内的弹丸综合散布密度必须是常数。

2最优瞄准点坐标模型

由最优函数Uo(x,z)中可近似确定炮弹的最优瞄准点坐标。为此假设炮弹射击数足够大，并引入射击密度函数N(ξx,ξz)，N(ξx,ξz)ΔξxΔξz表示位于区间Δξx×Δξz内的瞄准点数。把式(4)中的ln[1-p(x+ξxi,z+ξzi)/ω]近似用-p(x+ξxi,z+ξzi)/ω替代，可得

(16)

当瞄准点坐标的变化区间Δξxj、Δξzj足够小，设pj(x+ξxi,z+ξzi)为瞄点坐标位于区间Δξxj×Δξzj内的所有炮弹命中目标的平均概率，于是有

(17)

当Δξxj，Δξzj趋向无穷小时，式(17)变为

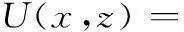
(18)

一般而言，未来空域窗大大超过炮弹的散布区域，因此可认为N(ξx,ξz)在p(x+ξx,z+ξz)不为零的区域为常数，并等于ξx=x,ξz=z时的值，因此式(18)可为

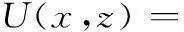
(19)

考虑了先前的近似替代，由式(7)可得

(20)

(21)

式(21)可以用于确定未来空域窗最优参数，使得实际上的射击密度最接近最优值。近似确定最优瞄准点坐标及分配给这个瞄点的炮弹数量可按如下方式完成。

(1) 如果瞄准点坐标指定

为总的瞄准点数，则分配给每个瞄准点的炮弹数量nij为

(22)

(2) 如果指定了分配给每个瞄准点的炮弹数量nij(i=1,…,a;j=1,…,b;a×b≤n)，则由式(22)组成的方程组求解瞄准点坐标ξxi,ξzj。

3毁伤目标概率

把最优函数Uo(x,z)代入式(8)，可得目标未被毁伤的最小概率Pn,0

(23)

由式(2)可得在未来空域窗射击体制下，可实现的毁伤目标概率的上界是

(24)

显然，当采用集火射击时，所有的炮弹的瞄准点相同，由式(2)可得集火射击时的毁伤目标概率

(25)

下面分析按文献[1]未来空域窗下的毁伤目标概率。此时2组误差等效为1组误差，有

归一化的瞄准点坐标(ξxi,ξzi)(i=1,…,h)为

(26)

(27)

4算例分析

n=180，360，720; k=0.2，0.4，0.6，0.8，1

把参数的中间取值定为基准值，也就是说，在每次计算中，参数中最多只有一个取非基准值，而其他的参数均取基准值。根据文献[1]，h=6。这样，在给定初值的条件下计算结果如表1所示。

表1　各种参数对未来空域窗的影响

根据计算结果，可得到如下结论。

(1)εx或εz增大，意味着炮弹间的相关误差增大，而炮弹间的相关误差主要是由目标定位误差造成的，目标机动越大，该误差越大，此时采用未来空域窗射击，相对于集火射击，其优势越大，所以未来空域窗射击体制主要用于对高机动目标的拦截。

(2)k或m增大，意味着目标的等效毁伤面积增大，未来空域窗射击和集火射击的效能都提高，但未来空域窗射击效率提高更大，这说明未来空域窗射击比较适合于大目标。

(3) 齐射的炮弹数量增大，未来空域窗射击和集火射击的效能都提高，但由于未来空域窗区域增大，其效能提高的程度大于集火射击情况，这说明未来空域窗射击要求的炮弹数量要达到一定值后才能采用。

(4)ω增大，即毁伤目标所需的炮弹数增大，未来空域窗区域减小，未来空域窗射击效率降低。

(5) 由文献[1]提出的未来空域窗，得到的毁伤目标概率明显低于未来空域窗射击毁伤目标概率上界，这说明这种未来空域窗优势并没有完全发挥出，有时还低于集火射击的效能，只有提高炮弹数量才可能高于集火射击的效能，其实在同等条件下，采用本文提出的未来空域窗模型射击效能高于集火射击。

5结论

以往提出的未来空域窗模型，忽略了炮弹间的相关误差，单纯从弹头的散布密度和散布概率来构造未来空域窗，并不能得到最优的未来空域窗，从算例可以看出，与最优解还有一定差距。而本文从毁伤目标效能的角度，给出了更优的未来空域窗模型，为未来空域窗射击体制的工程化应用提供了更坚实的基础。

参考文献：

[1] Hu J C, Guo Z. Mathematical description of future airspace window (FAW)[J].ActaArmamentarii, 1998, 19(4): 293-297. (胡金春,郭治.未来空域窗的数学描述[J].兵工学报,1998,19(4):293-297.)

[2] Lu X H, Li Q, Ouyang P. Rof in different weapons of the maneuvering target hit the theoretical analysis[J].FireControl&CommandControl,2013,38(3):8-11.(卢秀慧,李强,欧阳攀.高射速武器对不同机动目标的命中理论分析[J].火力与指挥控制,2013,38(3):8-11.)

[3] Liu H, Mei W, Shan G L. Analytical model of kill probability of future airspace window shooting[J].FireControl&CommandControl,2013,38(4):130-136.(刘恒,梅卫,单甘霖.空域窗射击毁歼概率解析计算模型[J].火力与指挥控制,2013,38(4):130-136.)

[4] Park K, Kang H, Kim C M. Sensitivity analysis of design parameters of an anti-aircraft gun for hit probability enhancement[J].JournalofMechanicalScienceandTechnology,2013,27(10):3043-3046.

[5] Liu Y W, Wang H X, An W. Hit probability analysis on imaging infrared guidance missile disturbed by laser[J].JournalofConvergenceInformationTechnology, 2012, 7(15): 437-444.

[6] Kumar D, Mishra R N. Angular orientation of anti-aircraft gun for interception of a moving air target[J].DefenceScienceJournal, 2009, 59(1): 3-14.

[7] Du Z, Wang C Z, Chen W C. Fast analytical model of cruise missiles penetration ship-based anti-missile system[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(11): 1449-1454. (杜政, 王朝志, 陈万春. 巡航导弹群突防舰载反导系统快速分析模型[J]. 北京航空航天大学学报, 2013, 39(11): 1449-1454.)

[8] Wang C C, Xie X F, Sun T, et al. Damage analysis of naval gun guided projectile to typical anti-ship missile in proximity mode [C]∥Proc.ofAppliedMechanicsandMaterialsConference,2013:385-386.

[9] Chen H B, Du Z H, Chen L M, et al. Remote anti-missile capability of gun-launched fuel-air-explosive projectile[J].JournalofNanjingUniversityofScienceandTechnology,2012,36(5):745-749.

[10] Xing C F, Li M Y, Wu L.Systemeffectivenessanalysisofshipborneweapons[M].Beijing: National Defense Industry Press,2007.(邢昌风,李敏勇,吴玲.舰载武器系统效能分析[M].北京:国防工业出版社,2007.)

卢发兴(1974-)，男，副教授，博士，主要研究方向为舰载指控及火控系统。

E-mail：lfx1974@163.com

贾正荣(1992-)，男，硕士研究生，主要研究方向为舰载火控系统。

E-mail：jzr451763650@sina.cn

吴玲(1976-)，女，副教授，博士，主要研究方向为舰载指控及智能决策技术。

E-mail：wul.nue@gmail.com

余戌曈(1990-)，男，硕士研究生，主要研究方向为舰载指控系统。

E-mail：yxtmcy0217@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141119.2233.013.html

Optimal model of future airspace window

LU Fa-xing, JIA Zheng-rong, WU Ling， YU Xu-tong

(ElectronicEngineeringCollege,NavalUniversityofEngineering,Wuhan430033,China)

Abstract:The shooting mode of future airspace window (FAW) is a gun shooting mode recently developed. In the existed studies, a feasible mathematical model of the FAW is provided with only one group error considered. With the correlated errors of projectiles taken into consideration and the killing probability set as an effectiveness index, the optimal model of the FAW is derived. Computation samples are carried out and the influence of the parameter variations on the FAW is analyzed. The results show the advantage of the proposed FAW model over the existed models.

Keywords:fire control system; firing theory; future airspace window (FAW); kill probability

作者简介：

中图分类号：TP 271

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.15

收稿日期：2014-09-11；修回日期：2014-11-03；网络优先出版日期：2014-11-19。