二重频高频雷达折叠杂波抑制算法

毛智能， 位寅生

(哈尔滨工业大学电子与信息工程学院， 黑龙江 哈尔滨 150001)



二重频高频雷达折叠杂波抑制算法

毛智能， 位寅生

(哈尔滨工业大学电子与信息工程学院， 黑龙江 哈尔滨 150001)

摘要：高频雷达系统中，远距离扩展杂波经距离折叠后，将淹没检测区域中的目标，为保证目标的检测质量，需对折叠杂波进行抑制。在发射二重波形重复频率信号下，提出了通过逻辑映射抑制杂波的方法。给出了参数设计准则，并分析了算法对杂波的抑制性能。仿真实验表明，在合适的信号参数下，该算法能够有效地抑制远距离折叠的扩展杂波。

关键词：高频雷达; 杂波抑制; 距离折叠杂波; 多普勒扩展杂波

0引言

传统的固定波形重复周期信号，其最大无模糊测距范围与最大无模糊测速范围存在固有矛盾，而高频雷达作用距离可达几千公里，远距离的电离层杂波经距离折叠回检测区域，淹没检测区域的目标，造成目标检测困难。

文献[1]中使用了一种非周期波形(nonrecurrent waveform，NRWF)，该波形在周期线性调频的基础上，对整个相参积累时间内的每个线性调频脉冲附加了一个二次型相位因子。利用该信号时，远距离的杂波每经过一次距离折叠都会附加多普勒偏移，通过控制二次型相位因子，可使远距离杂波出现在非关心的多普勒区间，即通过牺牲一部分多普勒检测区间，达到其余区间正常检测的目的。但对于高频雷达，扩展杂波经常会覆盖所有多普勒单元，此时该信号将失去应有的作用。文献[2]在NRWF基础上用空时自适应处理来抑制折叠杂波，当杂波多普勒扩展较小时能取得良好的效果，而当多普勒域扩展严重时，效果并不理想。文献[3-4]中利用高重频步进频率来实现折叠杂波抑制，然而这种信号在高频雷达中并不适用。而对多重频的研究多关注在利用多重频来实现最大无模糊测距/测速的扩展[5-7]，这些方法在每组重频信号完成目标检测后，再对检测所得的目标解模糊来扩展无模糊距离/速度。而在远距离扩展杂波背景下，目标检测环节受到限制，限制了该体制的应用。文献[8-9]在三重频的基础上设计滤波器来抑制特定频率段的杂波，不适用于高频雷达系统中的多普勒扩展杂波。此外多重频也在动目标检测用于扩展盲速[10-12]。文献[13-14]使用3组重频，先对距离折叠杂波进行抑制，之后再进行的目标检测，但其杂波抑制后仍有残留。

针对高频天波雷达在远距离折叠多普勒扩展杂波的特殊性，本文在发射二重频信号前提下提出了一种基于逻辑映射的杂波抑制算法。第1节给出了二重频信号的表达式以及对应的杂波抑制处理方法。第2节给出了对所发射信号的参数设计方案，并对基于逻辑映射折叠杂波抑制算法的输出信杂噪比(signal to clutter plus noise ratio, SCNR)和信噪比(signal to noise ratio, SNR)进行了理论分析。第3节通过实验仿真验证了所提方法的可行性、合理性。

1信号形式及杂波抑制原理

1.1信号形式

本文采用二重频线性调频连续波信号，信号形式如图1所示。

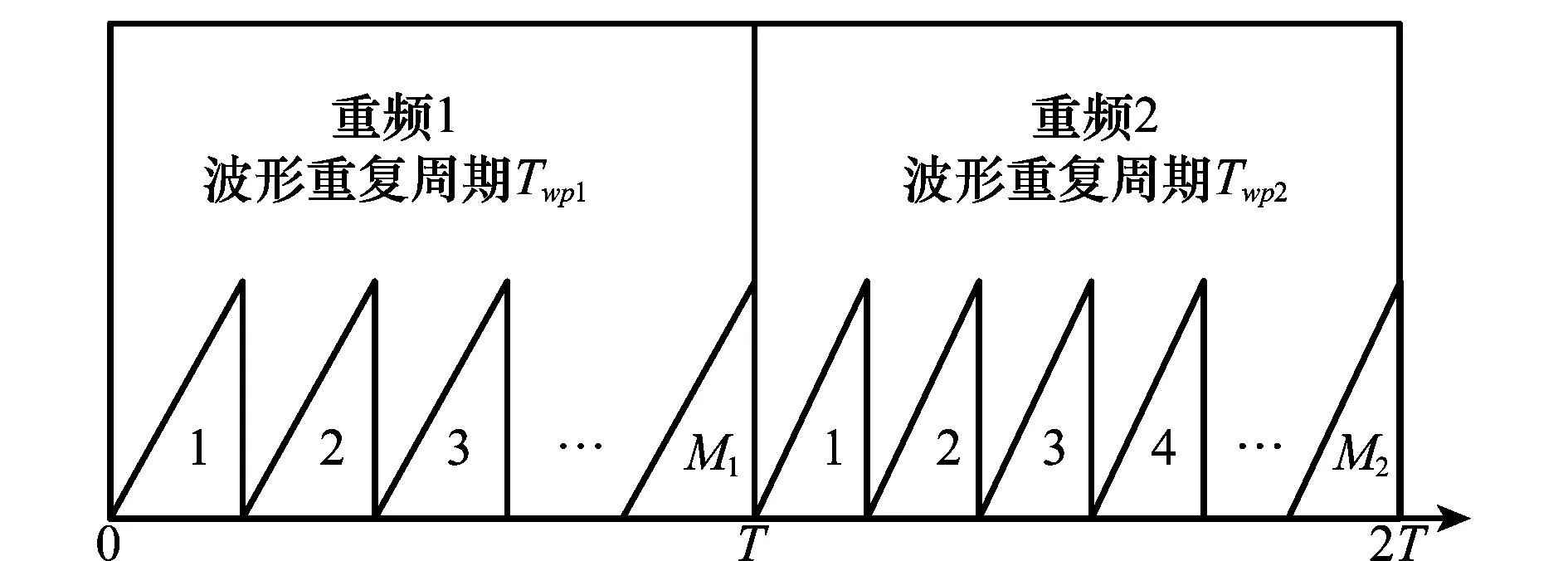
图1　二重频线性调频信号波形示意图

图1中，Twp1,Twp2为重频1、重频2的波形重复周期；M1,M2为重频1、重频2的积累脉冲数，且满足：

(1)

即各重频持续时间相同。从式(1)及图1中可以看出，二重频线性调频连续波信号将整个相参积累时间均分为2段，每段对应一个线性调频连续波。其信号表达式为

(2)

式中，f0为载频；u1(t)，u2(t)为重频1、重频2的线性调频脉冲，其表达式为

(3)

式中，ki为重频i的调频斜率且满足kiTwpi= B，即2组重频信号的调制带宽相同。

式(1)是为了保证2组重频信号具有相同的相参积累时间，以使得2组重频信号在距离多普勒处理后多普勒分辨单元尺度保持一致。而相同的调频带宽B可以保证2组重频信号在距离匹配处理后的距离分辨单元尺度保持一致，以方便后续处理。

1.2信号处理方案

式(2)描述了二重频线性调频连续波信号形式，可分为2组不同重频的线性调频连续波。因此，对于回波信号的处理可分为3步，如图2所示。第1步，对各组重频信号分别进行距离多普勒处理[15]；第2步，距离补偿；第3步，距离折叠杂波进行杂波抑制处理。本文仅考虑后两步。

图2　处理流程图

1.2.1距离补偿

距离补偿分2部分，第1部分是由于线性调频信号距离与多普勒耦合，多普勒频移对距离的估计引入一偏差，该偏差为

(4)

第2部分偏差是在重频1的持续时间内目标运动的距离，该距离分量为

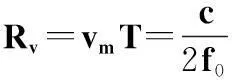
(5)

式中，vm为当前多普勒门对应的速度。

以第2组重频信号处理时刻目标所在的位置为参考标准，则需对第1组重频信号距离多普勒处理结果补偿第2部分距离偏移。则目标距离补偿公式为

(6)

式中，c为光速；Rm,fd为未补偿前某一单元的距离、多普勒频率；R为补偿后该单元的距离；i为重频序号；ki为第i重频的调频斜率。

1.2.2逻辑映射

记补偿后第i组重频的距离多普勒谱为RDi

(7)

则一个距离门代表的距离为δR=c/2fs，一个多普勒门代表的频率为δf=1/T。

记杂波抑制后的距离多普勒谱为RD

(8)

式中，Nr,Nd为所处理的距离门数、多普勒门数，满足

(9)

如果在某组重频距离多普勒谱的距离门nr与多普勒门nd中存在目标，则该目标也必定会在另一组重频距离多普勒谱的相应位置复现。而远距离杂波由于存在距离折叠，其在各重频中的距离门位置均不相同。因此，可以通过式(10)映射关系来完成对距离折叠杂波的抑制。

(10)

2信号参数设计要求

为达到理想的杂波抑制效果，需使得2组重频信号在距离多普勒处理后，经距离折叠后的杂波区域不发生重叠。

不妨设第1组重频的波形重复周期Twp1大于第2组的波形重复频率Twp2，则远距离折叠杂波在2组重频对应的距离处理结果中位置偏移的距离分辨单元数为

(11)

式中，k为距离折叠次数。

扩展杂波一般将连续覆盖某一区域，不妨设扩展杂波覆盖了Nc个距离分辨单元，为确保杂波在各重频中互不重叠，需满足

(12)

记

(13)

代入式(12)有

(14)

此外还需保证观测区域中目标无距离模糊，设Twp2=mΔT，其中m为正整数，则需有

(15)

由式(14)可以获得2组重频重复周期时差ΔT，确定ΔT后即可由式(15)计算最小正整数m，进一步可以得到2组重频的重复周期。

例如：若带宽B = 20kHz，Nc=40，检测区域目标最大距离Rmax=2 000km，由式(14)知

不妨取ΔT=2.4ms，代入式(15)可获得最小正整数m=6，则有Twp1=16.8ms，Twp2=14.4ms。

3输出SCNR分析

3.1输出SNR分析

若2组重频距离多普勒谱中距离门nr与多普勒门nd对应的单元均为纯粹的噪声，则该数据单元可表示为

(16)

式中，w表示噪声。

则该距离门nr与多普勒门nd映射后输出为

(17)

若目标出现在距离门nr与多普勒门nd，则该数据单元可表示为

(18)

式中，s表示信号。

映射后该距离门nr与多普勒门nd的目标输出为

(19)

可知输出SNR为

(20)

由式(20)可知，SNRout不小于最小的输入SNR。而对于同一目标而言，其SNR在短时内不会有太大的改变，因此SNRout可认为无损失。SNRout与输入SNR统计曲线如图3所示(统计次数MC=1 000)。

图3　无杂波环境下SNRout随输入SNR统计曲线

3.2输出SCNR分析

不妨设第1组重频距离多普勒谱中的距离门nr与多普勒门nd数据单元为远距离折叠杂波，则该数据单元可表示为

(21)

式中，c表示杂波。

由于远距离折叠杂波在2组重频中出现的位置存在偏移，因此在另一重频中对应位置处为噪声。因此经映射后该距离门nr与多普勒门nd的数据单元输出为

(22)

不妨设第1组重频距离多普勒谱中的距离门nr与多普勒门nd数据单元中存在目标，且被杂波掩盖，该数据单元可表示为

(23)

同理可知，在另一重频中对应位置处只存在信号与噪声，因此映射后输出为

(24)

输出SCNR为

(25)

同理，当杂波淹没第2组重频距离多普勒谱中的目标时，SCNRout等于第1组重频距离多普勒谱中相应目标的SNR。可见，当满足适当的信号参数时，理论上可以实现对折叠杂波的有效抑制。杂波环境下SCNRout随输入SCNR的统计曲线如图4所示(统计次数MC = 1 000)。

图4　杂波环境下SCNRout随输入SCNR统计曲线

4仿真结果

本实验仿真条件设置如下：信号载频 f0= 10MHz，调频带宽B=20kHz，远距离(Rc=2 850km)折叠杂波采用高斯型扩展杂波[16]，在距离与多普勒维均存在扩展，距离扩展方差σr=60km，多普勒扩展方差σf=10Hz，杂波仿真可参考文献[16]，两目标径向距离分别为330km、700km，径向速度均为v=3m/s，检测区域目标最大距离Rmax=2 000km。通过式(14)和式(15)，可选择一组合适的重频参数Twp1= 16.8ms，Twp2=14.4ms。每组重频相参积累时间T=40s。

图5(a)和图5(b)分别对应2组重频各自的距离多普勒谱。可看出，在第1组重频中，目标1已经被远距离折叠距离多普勒扩展杂波完全淹没。而在第2组重频中，由于信号重复频率的不同，使得远距离折叠杂波经距离折叠后与第1组重频对应的位置互不重叠。图5(c)为经过逻辑映射后的距离多普勒谱，可见在选择合适的参数下，经过逻辑映射后，2组重频距离多普勒谱中的远距离折叠多普勒扩展杂波均被有效抑制。

图5　折叠杂波抑制前后的距离多普勒谱

图6为目标所在多普勒门截面图，其中，图6(a)和图6(b)分别为第1重频与第2重频下目标所在多普勒门的距离谱，图6(c)为杂波抑制后的输出。从图中可以清楚地看到，距离折叠杂波在处理后已无杂波残余。即使在某一重频分组下目标被杂波完全淹没，经处理之后可以很轻松地将目标检测出来。需要留意的是，这种处理方法完全是盲处理，即在处理之前无需进行目标检测。

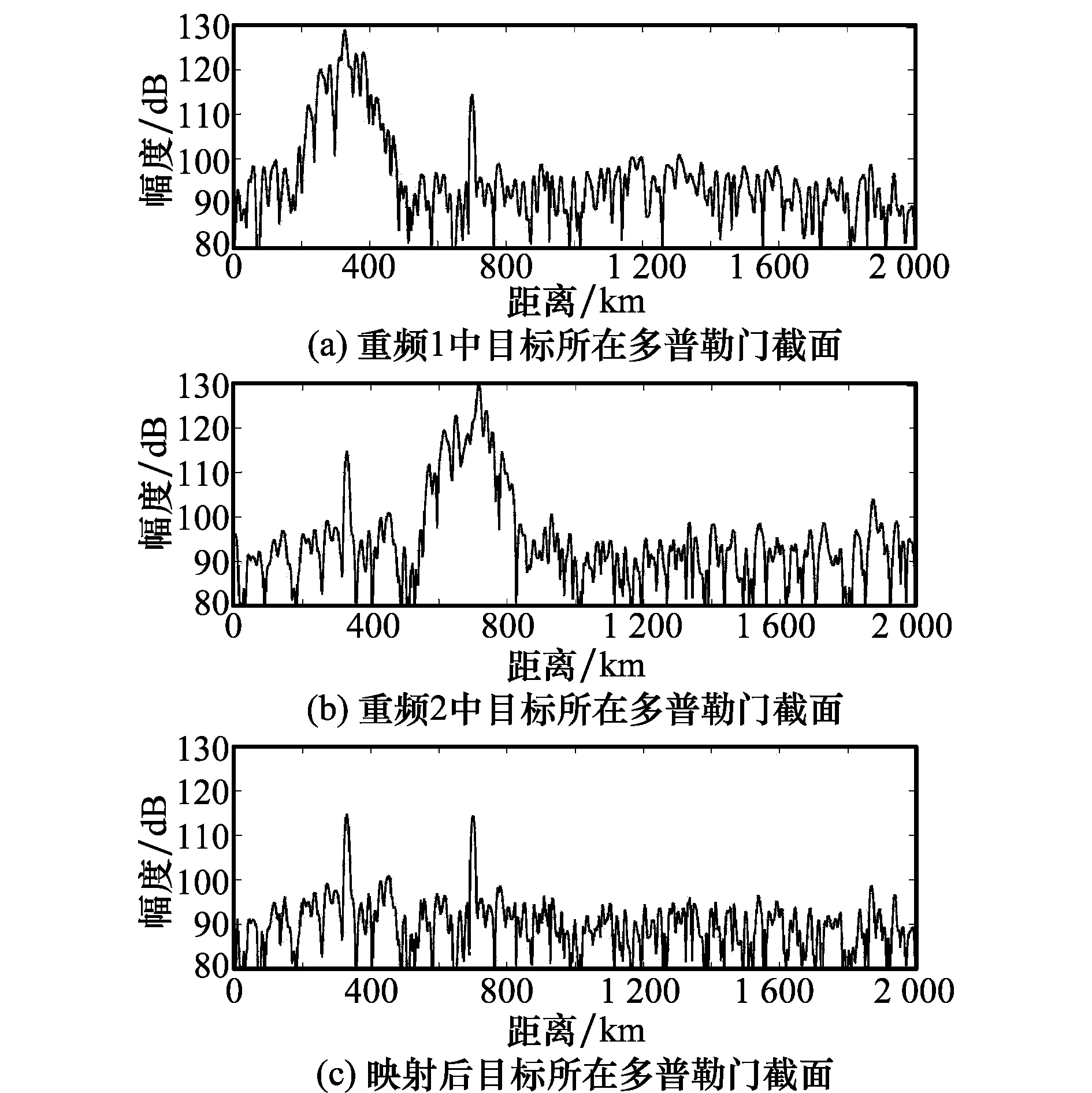
图6　目标所在多普勒门截面图

5结论

本文提出了一种二重频信号的折叠杂波抑制方法。通过对SNRout和SCNRout的推导，指出该方法对输入SNR几乎无损，而且在合适的参数设计条件下能够对距离折叠杂波有效抑制。当然该方法应用具有一定的局限性，要对距离折叠杂波有效抑制，对二重频信号的信号重频频率有一定的设计要求。仿真实验也验证了该方法能够有效抑制远距离折叠距离多普勒扩展杂波，但其多普勒分辨能力为具有相同积累时长的单一重频信号的一半。此外，在相同处理时间内，如果进一步增加重频数会降低多普勒分辨能力，但可以扩展无模糊多普勒检测区间。

参考文献：

[1] Clancy J T, Bascom H F, Hartnett M P. Mitigation of range folded clutter by a nonrecurrent waveform[C]∥Proc.oftheRadarConference, 1999:79-83.

[2] Lee W W, Krolik J L. Space-time adaptive processing for range-folded spread-Doppler radar clutter mitigation[C]∥Proc.oftheAcoustics,SpeechandSignalProcessing, 2011:2772-2775.

[3] Wang F X, Tang G F, He S S, et al. Severe clutter suppression in high PRF stepped-frequency radar[J].JournalofNationalUniversityofDefenseTechnology,2009,31(4):52-57.(王飞行,汤广富,贺思三,等.高重频频率步进雷达强杂波抑制[J].国防科技大学学报,2009,31(4):52-57.)

[4] Wang F X, Chen J J, Fu Q. A method of suppressing folded clutter in high PRF stepped frequency radar[J].SignalProces-sing,2010,26(3):388-393.(王飞行,陈建军,付强.高重频频率步进雷达抑制折叠杂波方法[J].信号处理,2010,26(3):388-393.)

[5] Duan J Q, He Z S, Han C L. Computationally efficient algorithm for resolving range and velocity ambi-guities in multiple PRF PD radars[J].JournalofUniversityofElectronicScienceandTechnologyofChina,2008,37(4):549-551.(段军棋,何子述,韩春林.高效的PD雷达多重频模糊分辨算法[J].电子科技大学学报,2008,37(4):549-551.)

[6] Nie S M, Zhang Z J, Ou J P, et al. A new method to reduce channel quantization error in resolving velocity ambiguity by PRF varied method[J].ModernElectronicsTechnique,2011,34(11):9-12.(聂胜猛,张泽建,欧建平,等.多重频解模糊中降低频道量化误差的新方法[J].现代电子技术,2011,34(11):9-12.)

[7] Ferrari A, Alengrin G, Theys C. Doppler ambiguity resolution using staggered PRF with a new chirp sweep-rate estimation algorithm[J].IEERadar,SonarandNavigation,1995,142(4):191-194.

[8] Harasawa Y, Sekiguchi T, Kirimoto T, Hamada N. A design method of clutter suppression filters with cascade connection using offset of zeros for staggered PRF[C]∥Proc.ofthe41stSICEAnnualConference, 2002:2955-2960.

[9] Nguyen C M, Moisseev D N,Chandrasekar V.A time domain clutter filter for staggered PRT and dual-PRF measurements[C]∥Proc.oftheGeoscienceandRemoteSensingSymposium,2007:3325-3328.

[10] McAulay R J. The effect of staggered PRF’s on MTI signal detection[J].IEEETrans.onAerospaceandElectronicSystems, 1973, 9(4):615-618.

[11] Sedivy P. Radar PRF staggering and agility control maximizing overall blind speed[C]∥Proc.oftheMicrowaveTechniques,2013:197-200.

[12] Arbabian M A, Bastani M H, Tabesh M. Optimization of PRF staggering in MTI radar[C]∥Proc.oftheIEEEInternationalConferenceonRadar, 2005:602-607.

[13] Musa M, Salous S. Ambiguity elimination in HF FMCW radar systems[J].IEERadar,SonarandNavigation, 2000, 147(4):182-188.

[14] Musa M, Salous S. Evaluation of multiple WRF-HF-FMCW radar waveform[C]∥Proc.ofthe8thHFRadioSystemsandTechniques, 2000:207-211.

[15] Levanon N, Mozeson E.Radarsignals[M].Wiley,2004.

[16] Ravan M, Riddolls R J, Adve R S. Ionospheric and auroral clutter models for HF surface wave and over-the-horizon radar systems[J].RadioScience, 2012, 47(3):1-12.

毛智能(1987-)，男，博士研究生，主要研究方向为新体制雷达理论与技术。

E-mail：nengzhimao@163.com

位寅生(1974-)，男，教授，博士，主要研究方向为雷达信号处理、阵列信号处理、雷达系统分析与设计。

E-mail：weiys@hit.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20141113.1619.004.html

Range-folded clutter suppression algorithm for high frequency radar using dual-WRF

MAO Zhi-neng， WEI Yin-sheng

(SchoolofElectronicsandInformationEngineering,HarbinInstituteofTechnology,Harbin150001,China)

Abstract:In the high-frequency radar system, the target of interest might be merged in the range-folded clutter. To get better detection performance, the range-folded clutter need to be suppressed. A logical-mapping clutter suppression method using dual waveform repetition frequency (WRF) is proposed. The selection criterion of signal parameters is given and the clutter suppression performance is also analyzed. Simulation results suggest that the clutter can be efficiently suppressed under proper signal parameters.

Keywords:high-frequency radar; clutter suppression; range-folded clutter; Doppler spread clutter

作者简介：

中图分类号：TN 957.51

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.12

收稿日期：2014-05-29；修回日期：2014-10-28；网络优先出版日期：2014-11-13。