应用于同步卫星通信的相控阵天线波束切换算法研究
2015-02-18向东游赵伊宁
石 彬,向东游,赵伊宁
(1.中国人民解放军92941部队,辽宁 葫芦岛 125001;2.北京机电工程研究所, 北京 100074;3.中国人民解放军装备学院 研究生管理大队,北京 101416)
应用于同步卫星通信的相控阵天线波束切换算法研究
石彬1,向东游2,赵伊宁3
(1.中国人民解放军92941部队,辽宁 葫芦岛 125001;2.北京机电工程研究所, 北京 100074;3.中国人民解放军装备学院 研究生管理大队,北京 101416)
摘要:提出了一种基于“地球系—地理系—载体系”的三坐标转换算法,解决了相控阵天线实时波束切换的需求,实现了搭载该相控阵天线的无人飞行器可在任意位置和任意姿态角与同步卫星进行不间断通信。通过数值模拟,证明该算法基本满足设计需求,具有一定的实际应用价值。
关键词:相控阵天线;波束切换;卫星通信
当今电子技术突飞猛进,在军用和民用科技领域都得到了极大的发展。目前,车载预警雷达、无线通信以及射频识别等技术的商业应用对天线的要求越来越高,尤其是对天线方向图灵活控制的需求越来越大,而相控阵天线所具有的对波速的灵活控制以及快速扫描等优点很好地适应了这种需求[1]。
本文以某大型无人飞行器所搭载的无源相控阵天线作为研究对象。该大型无人飞行器与固定的地球同步轨道卫星进行通信,采用相控阵天线实现飞行器任意位置、任意姿态飞行过程中其天线辐射波束始终覆盖该同步卫星,保证两者之间的不间断通信需求。该无源相控阵天线具有8个天线阵元,每个天线阵元在飞行器轴向上的辐射波束以40°为步长,总覆盖范围为-80°~80°。在飞行器径向上的辐射波束范围为45°,8个天线阵元围绕飞行器径向一周安装,实现飞行器径向360°全覆盖。
本文提出了一种切换算法, 实现相控阵天线的波束指向随着飞行过程中飞行器与同步卫星相对位置的变化,以及飞行器自身姿态的变化进行实时切换。
1涉及的几个坐标系
1.1地球直角坐标系(e系)
坐标轴用XeYeZe表示,原点在地球中心,Ze轴位于地轴北极,Xe轴位于赤道平面指向格林威治子午线,Ye轴位于赤道平面指向90°E[2]。该坐标系与地球固联随地球转动。
1.2地理直角坐标系(g系)
坐标轴用XgYgZg表示,原点位于载体质心,采用“北天东”系,Xg轴指向北,Yg指向天,Zg指向东。该坐标系原点位置代表载体位置。
1.3载体直角坐标系(b系)
坐标轴用XbYbZb表示,原点位于载体质心,Xb指向载体纵轴方向,Yb指向载体竖轴方向,Zb轴指向载体右翼。载体直角坐标系与载体固联,并随载体姿态变动而变动[3]。
载体直角坐标系与地理直角坐标系的相同点是原点都位于载体质心,不同点是载体直角坐标系与载体固联,随着载体姿态的变换而变化。
1.4姿态角定义约定
飞行器姿态角以载体坐标系为基础进行定义,包括俯仰角θs、航向角ψs和滚转角γs。俯仰角θs是飞行器纵轴 OXb与水平面XgOZg之间的夹角,纵轴位于水平面之上为正;航向角ψs是飞行器纵轴OXb在水平面XgOZg上的投影与OXg之间的夹角,由OXg轴逆时针转向飞行器纵轴OXb的投影线时为正;滚转角γs是OYb与包含飞行器纵轴OXb的铅垂面之间的夹角,从飞行器尾部顺OXb轴向前看,若OYb位于铅垂面的右侧,则滚转角为正。
2算法思路
波束切换算法的主要功能是实时计算卫星相对飞行器位置及姿态的二维方位角度,即径向角度α和轴向角度β,再根据角度切换天线相位。二维方位角的定义如图1所示。
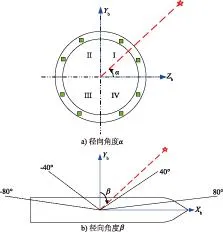
图1 卫星相对飞行器位置及姿态的二维方位角定义
同步卫星相对地球静止,因此描述无人飞行器位置(经度λm、纬度φm、海拔hm)及卫星位置(经度λs、纬度φs、海拔hs)可以以地球坐标系为统一的参考坐标系 。考虑到飞行器姿态参数,应将卫星坐标变换至飞行器载体坐标系下才能计算二维方位角,变换流程及输入参数如图2所示。
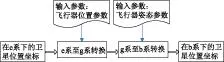
图2 同步卫星位置坐标变换流程
3算法实现
3.1变换矩阵
从e系到g系的坐标转换矩阵以及从g系到b系的坐标转换矩阵均可通过逐次旋转坐标轴的方式实现[4]。其转换矩阵如下所示:
(1)
(2)
3.2从极坐标系到直角坐标系的变换
卫星位置参数(λs,φs,hs)以极坐标系表示,考虑地球扁率,其在e系下的坐标通过下式转换:
(3)
3.3二维方位角计算
根据图2所示的流程,计算卫星在飞行器载体坐标系下的坐标(xsb,ysb,zsb)如下式所示:
(4)
根据图1所示的二维方位角定义,计算二维方位角(α,β)如下式所示:
(5)
4算法数值模拟测试及结果分析
根据式3~式5进行程序设计,对该算法进行了数字模拟,测试数据见表1。在式3中,采用的地球模型为WSG-84模型。

表1 算法数字模拟测试结果
由表1前3组样本数据表明,在飞行器参数保持不变时,卫星参数的变化很准确地反映在二维方位角的变化上;表1中间3组样本数据表明,当飞行器位置及卫星位置不变时,飞行器姿态的变化很准确地反映在二维方位角上;表1最后3组样本数据则是考虑一般情况下的测试结果。测试结果表明,该算法符合实际应用。
5结语
波束切换的基础实质上是求取同步卫星相对飞行器的二维方位角,“地球系—地理系—载体系”的三坐标转换算法则为二维方位角计算提供了基础。在具体硬件平台实现时,由于硬件数值计算精度的限制,在一些临近边界条件的场合会造成较大的角度误差,但对于实际应用,这些边界条件并不能得到满足;因此,该算法还是具有很大的应用价值和较为普遍的适用性。
参考文献
[1] 房亮.双极化相控阵天线单元研究[D].哈尔滨:哈尔滨工业大学,2013.
[2] 贾胜文.基于ARM7和FPGA的低成本小型捷联惯导系统的设计[D].西安:西北工业大学,2006.
[3] 张立.捷联惯导系统研究及仿真软件包开发[D].北京:北京航空航天大学,2000.
[4] 张士邈.适合高动态环境的捷联惯导系统高精度算法研究[D].西安:西北工业大学,2002.
责任编辑彭光宇
Research on Phase Array Antenna Beam Switch Algorithm Applied in Synchronous Satellite Communication
SHI Bin1,XIANG Dongyou2,ZHAO Yining3
(1.92941 Unit of PLA, Huludao 125001,China;2.Beijing Research Institute of Mechanical and Electrical Engineering,
Beijing 100074,China;3.Department of Graduate Management, Academy of Equipment of PLA, Beijing 101416, China)
Abstract:Propose the algorithm base on three coordinate transformations with earth-geography-basement to solve the demand of real-time beam switching of phase array antenna. With the algorithm, the uninterrupted communication between synchronous satellite and UAV with arbitrary position and attitude is implemented. The numerical simulation is presented and prove that the algorithm is useful and valuable in practical application.
Key words:phase array antenna, beam switch, satellite communication
收稿日期:2015-04-06
作者简介:石彬(1983-),男,工程师,大学本科,主要从事通信、遥测与遥控等方面的研究。
中图分类号:TJ 765.2
文献标志码:A
