基于T-S模糊模型的非均匀气隙永磁同步电动机混沌系统控制

孟　威，杨海峰

(国家电网辽宁省电力有限公司，辽宁 沈阳 110006)

基于T-S模糊模型的非均匀气隙永磁同步电动机混沌系统控制

孟威，杨海峰

(国家电网辽宁省电力有限公司，辽宁 沈阳 110006)

摘要：基于T-S模糊模型，给出了一种针对非均匀气隙永磁同步电动机(PMSM)混沌系统的控制方法。通过一个多时标变换，将转子磁场定向坐标系下的PMSM模型，变换成一种简单的无量纲模型。基于Lyapunov稳定性理论，设计了反馈控制器，实现了对非均匀气隙PMSM系统的混沌控制。

关键词：T-S模糊模型；非均匀气隙；永磁同步电动机；混沌；Lyapunov稳定性

模糊控制理论已经发展了约半个世纪，在模糊控制理论发展的不同阶段，形成了不同的主流模糊控制器设计方法，常用的模糊模型有模糊关系模型、T-S模糊模型、模糊基函数模糊模型、模糊动态模型以及模糊双曲正切模型等。其中，由T.Takagi与M.Sugeno首先提出的T-S模糊模型[1]将线性系统理论与模糊理论相结合来解决非线性系统控制问题，将整个非线性系统的控制看作是多个局部线性系统控制的模糊逼近，这不仅开创了模糊模型辩识的新方法，同时也为模糊控制系统的稳定性分析和设计提供了模型基础。T-S模糊模型是当前应用最为广泛的模糊模型，引起了广大研究者们的重视[2-6]。

作为一种应用广泛的电力传动系统驱动电动机，永磁同步电动机(PMSM)由于其结构简单、高效节能、调速范围宽和波纹转矩小等优点，在工业上得到越来越广泛的应用。已有研究表明，电动机传动系统在某些特定参数及工作条件下会呈现混沌行为，其主要表现为转矩忽大忽小、转速忽高忽低和系统出现不规则电流噪声等[7-8]。混沌的存在将严重影响电动机运行的稳定性，为保持电力传动系统运行的性能，需要抑制或消除电动机运行时出现的混沌现象，由此引出了电动机的混沌控制问题。对PMSM的控制研究在不断发展，相继出现了参数扰动控制法、纳入轨道法或强迫迁涉法、工程反馈控制法和智能控制法等。

本文将以非均匀气隙PMSM系统为研究对象，利用T-S模糊模型对其进行建模，进而设计控制代价小、物理上易于实现的控制器，分别实现PMSM的混沌控制与反控制，从而全面提高PMSM的工作性能。

1非均匀气隙PMSM混沌系统的模糊控制

1.1T-S模糊模型

根据下述描述考虑连续T-S模糊控制：

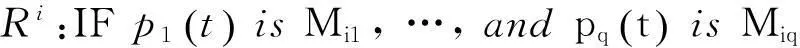
采用一个标准模糊推理策略，即运用单点模糊化、乘积推理和平均加权反模糊化，最后推断出的连续模糊T-S系统状态方程如下：

(1)

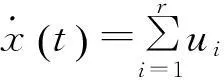
(2)

1.2非均匀气隙PMSM建模

根据d-q轴线，非均匀气隙的PMSM建模如下：

(3)

通过仿射变换和时间尺度变换，式3可以等效变换成：

(4)

式中，γ、σ、q为系统参数。

1.3非均匀气隙PMSM系统模糊建模

根据PMSM系统状态变量的有界性，可以得出：

(5)

式中，c1、c2、d1、d2的值可以在仿真中获得。

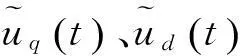
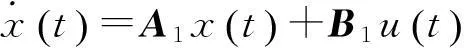
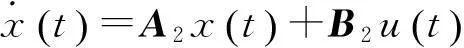
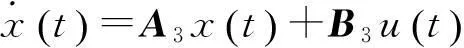
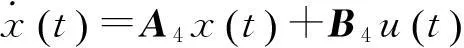
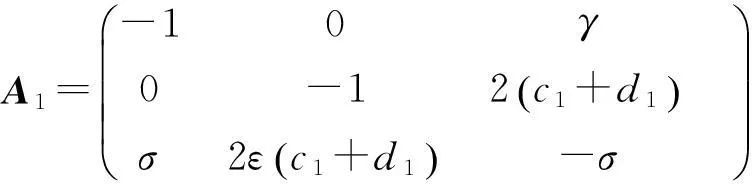
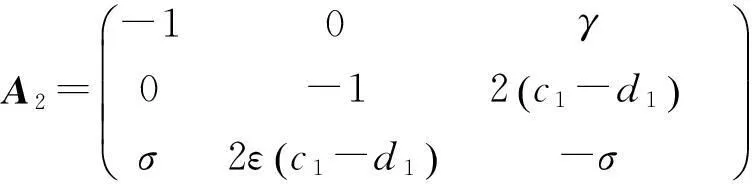
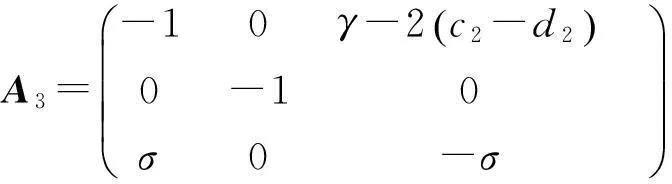
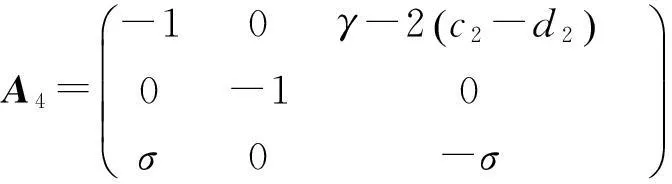
隶属度函数的选择如下：

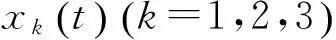
(6)

1.4非均匀气隙PMSM系统模糊控制

为了镇定式6所示的混沌系统，利用并行分布补偿(PDC)技术，设计如下形式的模糊控制器，其第i条模糊规则为：输入矩阵B，假设是满秩，可以选择一些适当的反馈矩阵Ki以满足下列公式：

Ai-BKi=H

(7)

式中，i=1,2,3,4；H是一个Huiwitz稳定矩阵。系统可以被精确的线性化为：

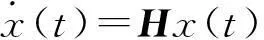
(8)

很明显，式8是渐近稳定。本文选择Ki=B-1(Ai-H)实现上述混沌系统渐进镇定。

2实例仿真

将上述非均匀气隙PMSM混沌系统进行仿真控制，未加控制的参数不确定非均匀气隙PMSM混沌系统的混沌吸引子如图1所示。当t=30 s时，开始施加控制，施加控制后的非均匀气隙PMSM混沌系统状态响应曲线如图2～图4所示。从图2～图4可以看出，受控的PMSM混沌系统很快稳定到零不动点上，达到了预期的控制效果。

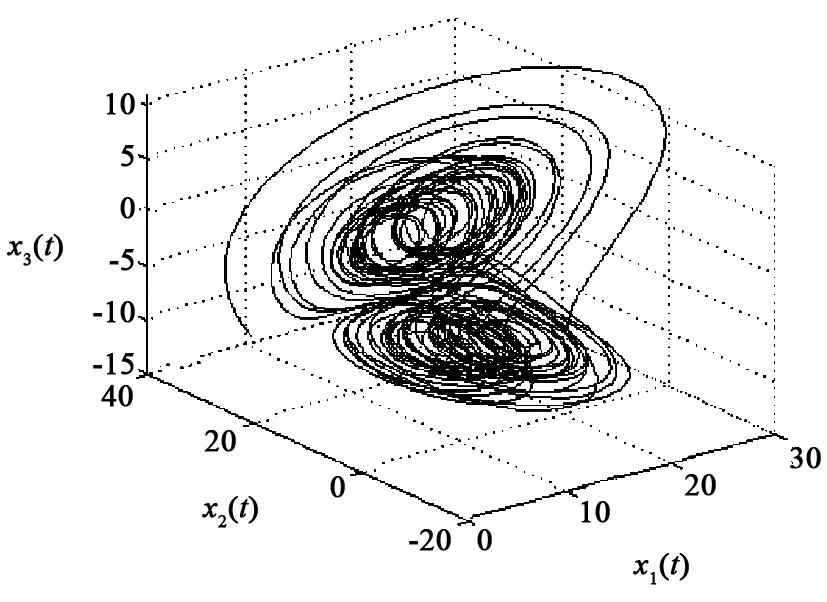
图1　非均匀PMSM模糊混沌系统的相轨迹

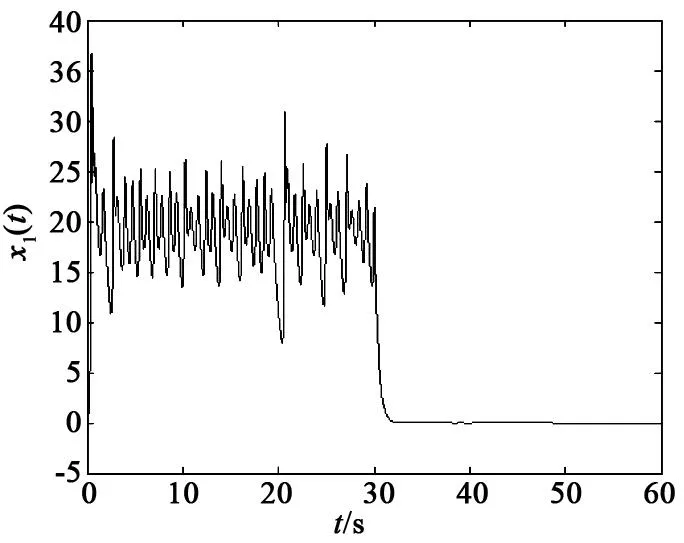
图2　受控PMSM混沌系统的状态响应曲线x1(t)

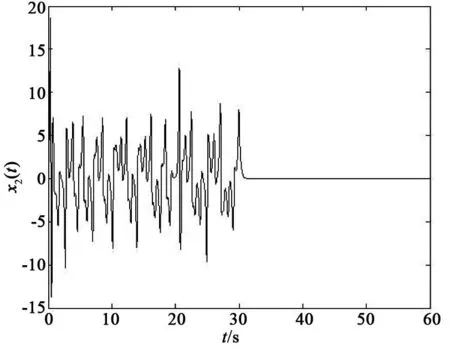
图3　受控PMSM混沌系统的状态响应曲线x2(t)

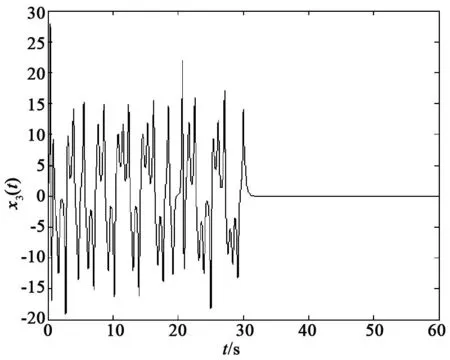
图4　受控PMSM混沌系统状态响应曲线x3(t)

3结语

本文给出了一种非均匀气隙PMSM混沌系统的同步控制方法。通过多时标的变换，将PMSM模型变换成一种无量纲的模型。再在PMSM混沌动态进行分析的基础上，基于Lyapunov稳定性理论，设计非均匀气隙PMSM混沌系统的自适应控制器，最终实现了对非均匀气隙PMSM的混沌同步控制。所设计的控制器结构简单，响应迅速，仿真结果说明了该方法的有效性。

参考文献

[1] Takagi T，Sugeno M．Fuzzy identification of systems and its applications to modeling and control[J]．IEEE Trans．Syst.，Man & Cybern.，1985,15(1):116-132．

[2] Wang H，Tanaka K，Griffin M. An approach to fuzzy control of nonlinear systems: stability and design issues [J]. IEEE Transactions on Fuzzy Systems，1996,4(1):14-23.

Chaotic System Control of Permanent Magnet Synchronous Motor with Nonsmooth Air-gap based on T-S Fuzzy Model

MENG Wei, YANG Haifeng

(State Grid Liaoning Electric Power Supply Co., Ltd.， Shenyang 110006，China)

Abstract：Based on T-S fuzzy model, give a control method of chaotic systems for permanent magnet synchronous motor with nonsmooth air-gap. Through a various time scale transformation, put the PMSM model with rotor field oriented coordinate system, and it is transformed into a simple non-dimensional model. Based on Lyapunov stability theory, design a feedback controller to achieve the chaos control of nonsmooth air-gap PMSM system.

Key words:T-S fuzzy model，nonsmooth air-gap，permanent magnet synchronous motors，chaos，Lyapunov stability

中图分类号：TP 273

文献标志码:A