变参数贝叶斯先验估计
2015-02-18李玮军孟昭为
李玮军,孟昭为
(山东理工大学 理学院,山东 淄博 255049)
变参数贝叶斯先验估计
李玮军,孟昭为
(山东理工大学 理学院,山东 淄博 255049)
研究了在非对称损失函数下独立随机变量序列的变化点的贝叶斯先验估计,以及在平方损失函数下变化点的贝叶斯先验估计和二者的比较,最终使在平方损失函数下得到的参数值较小。
贝叶斯估计;贝叶斯先验估计;非对称损失函数;变化点
1 问题背景
现有的数理统计分为经典学派和贝叶斯学派。贝叶斯统计与经典统计学的差别在于是否使用先验信息。贝叶斯估计不仅在统计学中占据着重要地位,在金融经济等其他领域也有着广泛的应用。贝叶斯先验估计是根据已有数据去估计未知参数的某些性质的方法。
20世纪50年代, Robbins在文献[1]中最早提出经验贝叶斯估计的概念,此方法把经典的统计方法和贝叶斯方法结合在一起,从此开启了统计学中一扇新的大门。近几十年来,国内外许多学者对经验贝叶斯做了很多研究和探索,不仅得到了丰富的理论成果,还得到了很多经验贝叶斯实际应用范例。文献[2]研究了连续性单参数指数族中参数的经验贝叶斯估计问题;文献[3]研究了离散型单参数指数族参数经验贝叶斯估计的渐近最优化问题;文献[4]研究了多元线性回归模型的经验贝叶斯估计问题;文献[5]研究了线性指数模型参数的经验贝叶斯估计问题。
然而在现实生活中,许多理论或者模型都考虑了统计模型的结构变化,从而忽略了在实际观测中的不稳定序列可能会使很多重要数据丢失的情况,这可能会导致错误的结果。
2 变化点的贝叶斯先验估计
假设X1,X2,…,Xm,Xm+1,…,Xn是一个至多一个变化点的随机变量序列,当
(1)
变化点m是一个未知的离散随机参数。然后假设尺度参数θ1和θ2,并且每个m都是先验独立的。
对于一个变化点,让p0表示零假设H0:m=n的后验概率,那么(1-p0)就是备择假设H1:m≠n的后验概率。
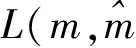
(3)
其中变量u决定损失函数的形状。
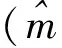
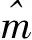
(4)
假设期望存在,那么K01就是满足H0的后验概率。

则

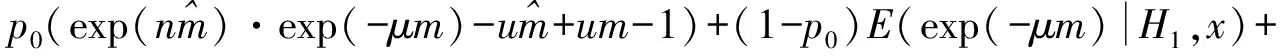

两边取对数得:
等式右边提出exp(-μn)可得
定理1得证。
推论1 在形式上变化点的贝叶斯先验估计反映了在备择假设H1:m=1,2,…,n-1形式下变化点的可能替代值的不确定性。

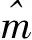

当K01>0,0 本文得到了在LINEX损失函数下独立随机变量序列的变化点的贝叶斯先验估计。值得注意的是,在LINEX损失函数下p=0的贝叶斯先验估计和在平方损失函数下得到的参数值比在LINEX损失函数下得到的要小。 [1] ROBBINS H.An Epirical Bayes approach to statistic[M]//Third Berkeley Symposium on Mathematical Statistics and Probability.Berkeley:University of California Press,1955:157-163. [2] SINGH R S.Empirical Bayes estimation in lebesgue exponential families with the rates near the best possible rate[J].Ann Statist,1979(7):890-902. [3] CHEN X R.Asymptotically optimal empirical Bayes estimation for para-Meter of one-dimention discrete exponential families[J].Ann Math,1983(4):41-50. [4] SINGH R S.Empirical Bayes estimation in a multiple linear regression model[J].Ann Inst Stat Math,1985,37:71-86. [5] GELFAND B P,SMITH A F M.Hierarchical Bayesian Analysis of Change point Problems[J].Applied Statistics,1992,41(2):389-405. [6] LU D K,BOSE S.A Bayesian Approach to Loss Robustness[J].Statistical Decisions,1998,16:65-87. [7] MICHEAS A C.Ranges of Posterior Expected Losses and Epsilon-Robust Actions[C]//Robust Bayesian analysis,Lecture notes monograph series.New York:Springer-Verlag,2000:145-160. [8] 刘次华.线性指数模型参数的经验贝叶斯估计[J].华中科技大学学报,2006(3):111-114. [9] 薛娇,常胜,邓丽.定时截尾样本下两参数指数-威布尔分布的可靠性Bayes估计[J].重庆理工大学学报(自然科学版),2014(8):132-139. [10]何朝兵,刘华文.IIRCT下几何分布参数多变点的贝叶斯估计[J].西南师范大学学报(自然科学版),2014(1):1-6. [11]朱宗元,穆良平,史代敏.基于动态线性模型的中国狭义货币需求及缺口的贝叶斯估计[J].数理统计与管理,2013(2):268-277. [12]齐华,王恒,刘军.可变周期的基于贝叶斯估计的TPSN改进算法[J].传感技术学报,2013(3):407-410. (责任编辑 何杰玲) Variable Parameters Bayesian Prior Estimate LI Wei-jun, MENG Zhao-wei (School of Science, Shandong University of Technology, Zibo 255049, China) This paper studied the estimation of Bayesian prior sequence of independent random variables under asymmetric loss function point, under squared loss function changes of Bayesian prior estimate and the comparison of the two. Eventually we got that under squared loss function, the parameter value is the smallest. Bayesian estimation; Bayesian prior estimate; asymmetric loss function; change point 2015-09-29 基金项目:山东省自然科学基金资助项目(ZR2013FM012) 作者简介:李玮军(1989—),男,山东淄博人,硕士研究生,主要从事应用统计研究。 李玮军,孟昭为.变参数贝叶斯先验估计[J].重庆理工大学学报(自然科学版),2015(12):143-146. format:LI Wei-jun, MENG Zhao-wei.Variable Parameters Bayesian Prior Estimate[J].Journal of Chongqing University of Technology(Natural Science),2015(12):143-146. 10.3969/j.issn.1674-8425(z).2015.12.024 O211 A 1674-8425(2015)12-0143-043 结束语
