基于bootstrap法的我国粮食产量回归分析
2015-02-18常振海张德生
刘 薇,常振海,张德生
(1.天水师范学院 数学与统计学院,甘肃 天水 741001;2.西安理工大学 理学院,西安 710054)
0 引言
粮食产量和粮食安全是人们一直关注的热点,学者们从不同角度讨论了粮食问题。因为能够用于统计分析的粮食年度数据较少,导致建立起的模型统计性质缺乏可信度,bootstrap方法给我们提供了增加样本量的便捷途径,关于bootstrap方法的应用研究近年来也热度不减[1~4]。将bootstrap方法用于研究粮食产量的文献所见不多,考虑到粮食产量前后几十年增加较快,可能存在距离均值较远的数据,本文结合较为稳健的M-估计[5],建立起关于我国粮食产量的bootstrap法回归模型。
1 基本知识与方法
考虑最简单的回归模型

在c=1.345时,它对正态数据的效率为95%。
(2)计算bootstrap法估计T*=β(S*)。
(3)重复(1)和(2)R次,本文取R=1999,这样得到的R个T*r(r=1,…,R)。
(4)利用R个T*r得到T的近似分布,从而可以得到待估计参数β的点估计,区间估计等统计量。
很显然,这种方法省去了对分布的假定及基于假定分布的统计推断,利用重复抽样来扩大样本量,建立起基于样本的统计分布。
2 实证分析
样本范围是1980~2012年共33个样本,初步选用变量为:
x1:农业机械总动力(万千瓦),
x2:受灾面积(千公顷),
x3:国家财政用于农业的支出(亿元),
x4:有效灌溉面积(千公顷),
x5:农用化肥施用折纯量(万吨),
x6:农村用电量(亿千瓦小时),
x7:粮食作物播种面积(千公顷),
Y:粮食产量(万吨),
数据来源于国家统计局网站。计算主要基于R语言。
自变量个数相对于样本个数来说较多,都选入模型显然不合适,为了选取对粮食产量有重要影响的因素,我们首先对这些自变量进行了降维分析,结果见图1。

图1 因子分析碎石图

图2 最大方差法因子旋转图
从图1能看出,提取两个因子,方差累计贡献率就达到了88.95%,这样,在这7个自变量中抽取出两个公因子,仅损失约11%的信息,效果还是很不错的。为了能更加清晰地显示提取的两个因子及其实际代表意义,我们做了最大方差法因子旋转,结果见图2。
从图2中能看出,变量x1,x3,x4,x5,x6代表了第一因子,x2,x7代表了第二因子。我们结合这些变量的实际意义,很容易看出第一因子与粮食单位面积产量有关,第二因子于粮食作物播种面积有关。进一步分析,在第一因子中的变量,对粮食产量影响最大的因素是x5,在第二因子的变量中则是x7。因此,我们分别以这两个变量为自变量,建立回归模型,同时为了便于比较自变量对因变量的贡献大小,这里首先对数据进行了中心化处理,处理后的变量分别称为zx5,zx7,zy,结果见表1(前4列)。

表1 M-估计结果
从表1中的t值能看出,系数是显著的,不过这个推断是基于大样本去推断的,很显然,稳妥起见,需要扩大样本量,采用bootstrap方法,结果见表1最后三列,这里的偏差和标准误差分别是

和表1中M-估计方法相比,bootstrap M-估计方法的系数几乎没什么改变,偏差很小,标准误略有增大,这个可能和离群值有关系,后面再讨论离群值的问题。这些bootstrap方法的估计系数分布见图3。

图3 bootstrap法的M-估计系数分布
从图3能看出,zx5系数接近于正态分布,尾部稍有点厚,zx7系数明显右偏,和正态分布相去甚远。在预测中这两个系数的关系可用图4来显示。
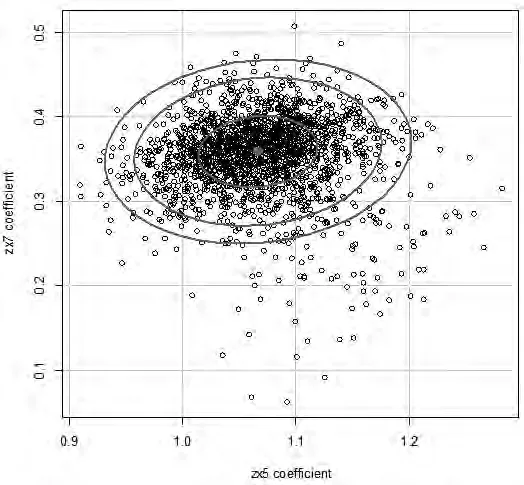
图4 两个系数的联合分布散点图
从图4能看出,这两个系数近似于不相关,说明在对zy预测时它们相对独立,这和开始我们采用降维的方法选取的变量结论是一致的。有了它们各自的分布和联合分布,我们就可以计算这些系数的M-估计区间,结果见表2。

表2 bootstrap法的M-估计区间
从表2能看出,系数zx5的三种区间结果相差不是很大,和该系数的分布近似于正态分布有关系,但系数zx7的则相差较大,图3中显示了其分布左尾较长,这个结果和图3中呈现的分布相一致,比较来看,显然BCa区间的结果更加可信。
这样,建立起的基于bootstrap法和M-估计方法的回归模型为

比较起见,我们将基于普通最小二乘方法的回归结果列出,见式(5)。

比较式(4)和(5),M-估计方法调低了农用化肥施用折纯量对粮食产量的影响,同时增加了粮食作物播种面积的影响。式(4)中系数的t值更大,标准误更小,说明M-估计更可靠。从回归结果看,在固定一个自变量的情形下,农用化肥施用折纯量和粮食作物播种面积每增加一个单位,粮食产量将分别增加1.0645和0.3612个单位,说明化肥在粮食种植中的作用较大,在我国经济快速发展的形势下,播种面积增加较为困难,重视化肥的使用将有助于粮食产量的增加。模型拟合的残差见图5。

图5 回归拟合的残差
从图5能看出,1980年、1981年和2003年的数据明显偏离样本均值,说明原始数据中可能存在异常值,为了直观显示每个观测点对系数的影响,采用Jackknife-after-Bootstrap方法,结果见(图6)。

图6 Jackknife-after-Bootstrap方法散点图
从图6能看出,观测点1(1980年),2(1981年)增大了系数zx5,减小了系数zx7,而点33(2012年)则使两个系数均增大。对照原始数据去看,因为我国粮食产量在近30年来增加较快,所以从数据上就使得1980年和1980年的粮食产量数据显得异常,而第24个数据(2003年)是近些年来粮食产量唯一比上一年下降的年份,所以也显得异常,再有就是第33个数据(2012年)也显示异常,说明去年的粮食产量数据较大,或者说距离均值较远,也说明我国粮食产量持续增高。
3 结论
(1)在对粮食产量有众多影响的因素中,经过降维分析,最终我们选取出了两个主要的因素,即x5:农用化肥施用折纯量(万吨)和x7:粮食作物播种面积(千公顷),同时为了能够比较这两个因素对粮食产量的影响大小,我们对数据进行了中心化处理。
(2)因为样本观测值只有33个,实际中又不可能增加,为了得到待估计系数的优良统计性质,我们采用了近些年来较为流行的bootstrap方法来增加样本量,同时采用较为稳健的M-估计方法,得到了回归结果。
(3)从回归结果看,在固定一个自变量的情形下,农用化肥施用折纯量和粮食作物播种面积每增加一个单位,粮食产量将分别增加1.0645和0.3612个单位,说明化肥在粮食种植中的作用较大,在我国经济快速发展的形势下,播种面积增加较为困难,重视化肥的使用将有助于粮食产量的增加。
(4)最后,基于Jackknife-after-Bootstrap方法,并结合残差对粮食产量进行了异常值分析,结果显示观测点1(1980年),2(1981年)增大了系数 zx5,减小了系数 zx7,而点33(2012年)则使两个系数均增大。对照原始数据去看,因为我国粮食产量在近30年来增加较快,所以从数据上就使得1980年和1980年的粮食产量数据显得异常,而第24个数据(2003年)是近些年来粮食产量唯一比上一年下降的年份,所以也显得异常,再有就是第33个数据(2012年)也显示异常,说明去年的粮食产量数据较大,或者说距离均值较远,也说明我国粮食产量持续增高。
[1]Peter H,Joel H.A Simple Bootstrap Method for Constructing Nonparametric Confidence Bands for Functions[J].The Annals of Statistics,2013,41(4).
[2]Michael P.F,Erica H B,Michael A.P.Pointwise Confidence Intervals for A Survival Distribution With Small Samples or Heavy Censoring Biostat[J].Biostatistics,2013,14(4).
[3]Hoai T T,France M,Nicholas H.G.H.A Comparison of Bootstrap Approaches for Estimating Uncertainty of Parameters in Linear Mixed-Effects Models[J].Pharmaceutical Statistics,2013,12(3).
[4]刘薇,常振海.基于自助法的统计泛函估计比较研究[J].统计与决策,2013,(2).
[5]Huber P J.Robust Regression:Asymptotic Conjectures and Monte Carlo[J].Ann.Statist,1973,1(5).
