基于海明距离和TOPSIS的直觉模糊数排序法

谭吉玉，朱传喜，张小芝，朱 丽

（南昌大学理学院，南昌330031）

0 引言

Atanassov于1983年对传统的模糊集进行了拓展，提出了直觉模糊集[1,2]的概念。由于直觉模糊集同时考虑了隶属度、非隶属度和犹豫度三方面的信息，因此，它比传统的模糊集能够更细腻地描述和刻画客观世界的模糊本质。Gau和Buehrer[3]定义了Vague集的概念。但是Bustince和Burillo[4]指出Vague集实质上就是直觉模糊集。直觉模糊集理论自提出以来，受到了学者们的极大关注，并已广泛应用于决策分析、医疗诊断、模式识别等诸多领域。徐泽水研究了决策者对方案有偏好的直觉模糊多属性决策问题[5]。定义了加型一致性直觉判断矩阵和积型一致性直觉判断矩阵等概念,并且分别利用两种转换函数建立了简洁的线性规划模型,给出了一种直觉模糊环境下对方案有偏好的多属性决策途径.Szmidt和Kacprzyk[6]基于直觉模糊集的几何解释提出了直觉模糊集的距离测度，结果表明在计算直觉模糊集的距离时，第三个参数即犹豫度不能省去，否则会导致不准确的结果。基于直觉模糊集的几何解释模型，Szmidt和Kacprzyk[7]还提出了非概率型直觉模糊集的熵测度公式。Li和Cheng[8]提出了直觉模糊集的相似性测度并应用于模式识别。

在直觉模糊多属性决策问题中，直觉模糊数的排序起着非常重要的作用。Chen and Tan[9]提出了直觉模糊数得分函数的概念。后来,Hong和Choi[10]指出得分函数有时候无法区分两个明显不同的直觉模糊数，如（0.6,0.3）与（0.5,0.2），它们的得分函数都是0.3，为了解决这种无法比较的问题，他们提出了精确函数的概念。然而，基于得分函数和精确函数的比较方法，得分函数处于绝对优先的地位，迫使得分函数小一点点，而精确函数大很多的直觉模糊数较小，如A=(0.5,0.3)和 B=(0.4,0.1999)(见文献[11])。直觉模糊数的排序问题引起了国内学者的浓厚兴趣，提出了各种各样的新的得分函数。本文从完全赞成(正理想点)和完全反对(负理想点)两个极端直觉模糊数进行分析，引入传统的TOPSIS思想，分别计算任意一个直觉模糊数与正理想点和负理想点的海明距离，然后计算相对于正理想点的相对贴近度，相对贴近度大的直觉模糊数就较大。基于新的排序指标，利用直觉模糊优先加权平均算子(IFPWA)算出其关联属性权重向量，进而计算各备选方案的集结结果，对最终的集结结果运用新的排序指标进行排序和择优，最后，通过实例说明了该方法的有效性。

1 直觉模糊集的基本理论

定义1[1,2]设X是一个非空集合，X上的直觉模糊集定义为

其中μA(x)和νA(x)分别为X中元素x属于A隶属度和非隶属度，即

并且对任意的x∈X，有 0≤μA(x)+νA(x)≤1.另外πA(x)=1-μA(x)-νA(x)表示X中元素x属于A的犹豫度。

定义2[9]设α=(μ，ν)为一个直觉模糊数，则称：

为α的得分函数，其中s(α)∈[-1，1]。

定义3[10]设α=(μ，ν)为一个直觉模糊数，则称：

为α的精确函数,其中h(α)∈[0，1].

定义4[12]设αj=(μj，νj)(j=1，2，...，n)为一组直觉模糊数，且设IFPWA:Θn→Θ，

定义5[6]设X={x1，x2，...，xn},A和B为定义在X上的直觉模糊集，则A和B之间的标准海明距离定义为：

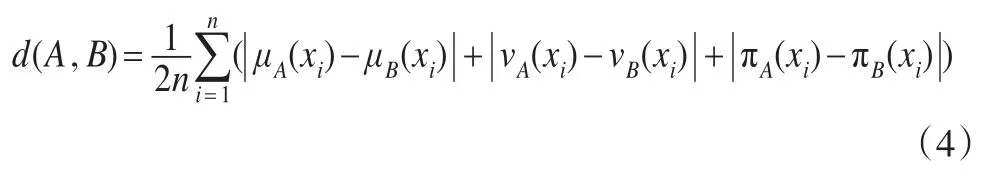
2 直觉模糊数的排序指标

为了方便起见，称α=(μ，ν)为直觉模糊数．记Θ为全体直觉模糊数的集合，显然,α+=(1，0)是最大的直觉模糊数,α-=(0，1)是最小的区间直觉模糊数。对任意一个直觉模糊数α=(μ，ν),有α-≤α≤α+。由定义1.5，我们可以计算任意一个直觉模糊数α=(μ，ν)与最大直觉模糊数α+=(1，0)和最小直觉模糊数α-=(0，1)的标准海明距离，我们分别用d+和d-来表示：

基于TOPSIS原理，我们给出任意一个直觉模糊数α相对于最大的直觉模糊数α+的相对贴近度的概念。

定义6设α=(μ，ν)为一个直觉模糊数，d+和d-分别为α与α+=(1，0)和α-=(0，1)之间的标准海明距离，则α相对于最大的直觉模糊数α+的相对贴近度为：

显然，C(α)的值越大，直觉模糊数α就越大。

性质1设α=(μ，ν)为一个直觉模糊数，C(α)具有如下性质。

（1）C(α)∈[0，1]，且C(α+)=1，C(α-)=0;

（2）当直觉模糊数α退化为普通的模糊数，即μ+v=1时，C(α)=μ；

（3）C(α)+C(αC)=1，αC为α的补集。

定理1直觉模糊数的贴近度C(α)随着隶属度μ的增加而增加，随着非隶属度ν的增加而减小。

定理2直觉模糊数的贴近度C(α)同时蕴含了得分函数和精确函数的排序原理。

证明：将函数f(μ，ν)改写为：，将得分函数s=μ-ν代入函数中得，，则f(μ，s)关于得分函数s的增函数.即直觉模糊数的得分值越大，f(μ，ν)的值也越大。

将函数f(μ，ν)改写为，当得分函数相等，即μ-ν是某一个常数时，将h=μ+v代入函数得，说明当得分函数相等时，f(μ，ν)是关于精确函数h的增函数。

综上所述，直觉模糊数的贴近度将随着隶属度的增加而增加，随着非隶属度的增加而减小；随着得分函数的增加而增加，当得分函数一样时，又会随着精确函数的增加而增加.因此，直觉模糊数的新的排序指标能蕴含得分函数和精确函数的排序原理，克服了应用得分函数和精确函数的排序法中得分函数处于绝对优先地位的不足。

3 属性间具有优先级别关系的直觉模糊多属性决策方法

对于某个属性间具有优先级别关系的直觉模糊多属性决策问题，设有m个备选方案A={A1，A2，...，Am},其中Ai表示第i个决策方案;决策方案的属性集合为G={G1，G2，...，Gn},属性间具有优先序关系:G1＞G2＞...＞Gn。方案Ai(i=1，2，...，m)在属性Gj(j=1，2，...，m)下的属性值为直觉模糊数,用αij=(μij，νij)表示,满足0≤μij≤1,0≤νij≤1,且μij+νij≤1。其中μij表示方案Ai对属性Gj的满足程度。νij表示方案Ai对属性Gj的不满足程度。收集所有决策信息可以建立直觉模糊决策矩阵D=(αij)m×n。下面给出求解属性间具有优先级别关系的直觉模糊多属性决策问题的具体步骤：

步骤 1由式(5)计算αij(i=1，2，...，m;j=1，2，...，n)的贴近度作为αij的得分。

步骤2计算Tij的值如下：

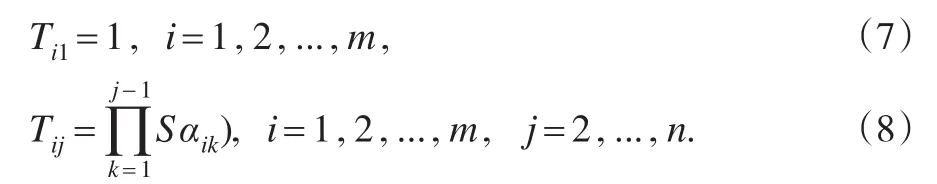
步骤3用直觉模糊优先加权平均(IFPWA)算子集结所有的αij(j=1，2，...，n)。

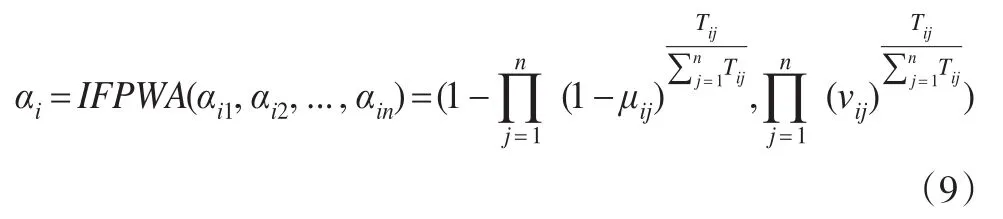
步骤4 由公式(5)计算各方案集结结果αi(i=1，2，...，m)的贴近度。

步骤5按各方案集结结果的贴近度大小对备选方案进行排序和择优。

4 实例分析

考虑一个家庭欲购买一台冰箱，现有五种品牌冰箱Ai(i=1，2，3，4，5)可供选择，用户选取了六项指标作为选择购买哪一款冰箱的标准。即为：G1:安全性;G2:制冷性能;G3:结构性;G4:可靠性;G5:经济性;G6:美观性。且六项指标间具有优先序关系:G1＞G2＞G3＞G4＞G5＞G6。用户通过对五种品牌冰箱在各评价指标下的满意度和不满意度得到直觉模糊决策信息矩阵D=(αij)5×6(见表1)。下面由本文所提出的方法确定最佳选择。

表1 直觉模糊决策矩阵D

步骤1由式（6）计算αij(i=1，2，...，m;j=1，2，...，n)的贴近度作为αij的得分,如

表2 得分矩阵S

步骤2用式（7）和（8）计算Tij的值，结果如下:

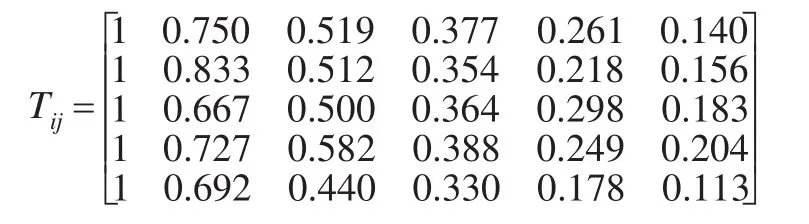
步骤3用(9)式集结所有直觉模糊数得到各备选冰箱的综合直觉模糊数，如：

步骤4由公式（5）计算各方案集结结果αi(i=1，2，...，m)的贴近度,如

步骤5根据第四步的计算结果进行排序,即五种品牌冰箱的综合排名为：

A2＞A4＞A3＞A1＞A5.因此,A2为最佳选择。

5 结论

基于直觉模糊集的海明距离,结合传统的TOPSIS思想,提出了一种新的直觉模糊数的排序指标.新的排序指标能够蕴含传统得分函数和精确函数的排序原理,克服了传统排序方法中得分函数处于绝对优先地位的不足。基于新的排序指标,利用直觉模糊优先加权平均算子(IFPWA),提出了一种属性间具有优先级别关系的直觉模糊多属性决策方法。最后,通过实例分析验证了所提出方法的有效性。

[1]Atanassov K.Intuitionistic Fuzzy Sets.[J]In:Sgurev V ed.VII-ITKRs Session,Sofia,J，1983，（6）.

[2]Atanassov K.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,(20).

[3]Gau W L,Buehrer D J.Vague Sets[J].IEEE Transactions on Systems,Man,and Cybernetics,1993,(23).

[4]Bustince H,Burillo P.Vague Sets Are Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1996,79(3).

[5]徐泽水.直觉模糊偏好信息下的多属性决策途径[J].系统工程理论与实践,2007,(11).

[6]Szmidt E,Kacprzyk J.Distances Between Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,2000,(114).

[7]Szmidt E,Kacprzyk J.Entropy for Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,2001,(118).

[8]Li D F,Cheng C T.New Similarity Measures of Intuitionistic Fuzzy Sets And application to Pattern Recognitions[J].Pattern Recognition letters,2002,(23).

[9]Chen S M,Tan J M.Handing Multicriteria Fuzzy Decision-Making Problems Based on Vague Set Theory[J].Fuzzy Sets and Systems,1994,(67).

[10]Hong D H,Choi C H.Multicriteria Fuzzy Decision-Making Problems Based on Vague Set Theory[J].Fuzzy Sets and Systems,2000,(114).

[11]Dymova L,Sevastjanov P,Tikhomenko A.Two-Criteria Method for Comparing Real-Valued and Interval-Valued Intuitionistic Fuzzy values[J].Knowledge-Based Systems,2013,(45).

[12]Yu D J.Intuitionistic Fuzzy Prioritized Operators And Their Application In Multi-Criteria Group Decision Making[J].Technological and Economic Development of Economy,2013,19(1).