深层凝析气井临界携液模型优化研究

周 朝，吴晓东，刘雄伟，黄 成，汤敬飞

(1.中国石油大学，北京 102249；2.中国石化西北油田分公司，新疆 阿克苏 842017)



深层凝析气井临界携液模型优化研究

周 朝1，吴晓东1，刘雄伟2，黄 成2，汤敬飞1

(1.中国石油大学，北京 102249；2.中国石化西北油田分公司，新疆 阿克苏 842017)

以Turner模型为代表的临界携液流量模型在预测积液位置和表面张力方面均存在不足，导致积液预测结果与凝析气井实际情况偏差较大。为提高积液预测精度，考虑临界携液流量和表面张力沿井筒的差异分布，取井筒中临界携液流量的最大值作为积液判断标准，并根据不同温度、压力条件计算对应的表面张力。同时，考虑井筒中存在气体、凝析油和地层水三相，建立凝析气井井筒温压耦合计算模型。实例验证表明，改进后的4种临界携液流量模型与原始模型相比，均提高了积液预测精度，其中改进的李闽模型预测精度提高的幅度最大，预测精度最高，适合于雅克拉—大涝坝深层凝析气井的积液预测。该研究对现场开展积液判断和排液工艺优选具有指导意义。

凝析气井；积液预测；临界携液流量；模型优化；温压耦合

0 引 言

气井积液是气藏开发过程中经常面临的问题。对于凝析气井，井筒中的产出液会导致压力损失，当产出气体不能将井筒内液体全部带出时，井筒中出现积液，影响气井的正常生产，降低最终采收率，严重时将导致气井停喷[1]。凝析气井临界携液流量的准确计算是预测积液和优选排液采气工艺的基础。以Turner模型为代表的临界携液流量模型在预测积液位置和确定表面张力方面均存在不足。结合雅克拉—大涝坝深层凝析气藏实例，对各模型的局限进行分析并改进，最终提高积液预测精度。

1 模型回顾

为了准确预测气井临界携液流量，国内外学者进行了大量研究工作。Duggan提出一种现场统计得到的经验方法[2]，Turner等人建立了计算垂直井筒临界携液流量的液滴模型[3]，此后，众多学者对Turner模型进行了修正和改进[4]。

积液预测常用的Turner、Coleman、李闽和杨川东模型的临界携液流速均可写为：

(1)

式中：ucr为临界携液流速，m/s；α为系数，Turner、杨川东模型取值6.6，Coleman模型取值5.5，李闽模型取值2.5；σ为表面张力，N/m；ρl为液体密度，kg/m3；ρg为气体密度，kg/m3。

临界携液流量公式为：

(2)

式中：qcr为标准状况下临界携液流量，104m3/d；A为油管面积，m2；p为压力，MPa；T为温度，℃；Z为气体偏差系数。

4种模型的主要差异见表1。

2 模型分析与改进

以上4种积液预测模型虽然在现场得到了广泛的应用，但是依然存在一些缺陷。

(1) 模型只考虑了井口或者井底条件下的临界携液流量计算，而没有考虑临界携液流量沿井筒的差异分布。实际上，临界携液流量在井筒中的分布与深度、温度、压力密切相关[5]。例如雅克拉—大涝坝深层凝析气藏3口井的井筒压力分布如图1所示，井筒临界携液流量分布(李闽模型)如图2所示。可以看出，Y4、D1和K8井的最大临界携液流量分别出现在井底、井深600 m和井口处。因此，计算临界携液流量时必须考虑其沿井筒的差异分布，取井筒中的最大临界携液流量作为积液判断标准。

表1 临界携液流量模型比较

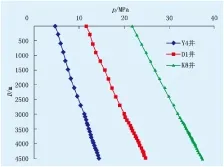
图1 井筒压力分布

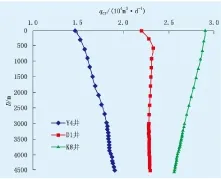
图2 井筒临界携液流量分布

(2) 4种模型在现场应用时均视表面张力为定值。而通过对雅克拉—大涝坝凝析气井分析可知(图3)，表面张力受井筒压力、温度以及凝析油和地层水含量的影响，沿井深差异分布。由图4可知，随着表面张力的变化，临界携液流量也随之变化，可见表面张力取定值会造成临界携液流量计算偏差，对于高压气井(如K8井)偏差更大，并且井底偏差大于井口偏差。所以应考虑表面张力沿井筒的差异分布，根据不同的温压条件分别计算。

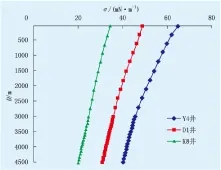
图3 井筒表面张力分布

图4 表面张力对临界携液流量的影响(K8井)

凝析气井井筒中的液相包括凝析油和地层水，可以根据Abdul-Majeed和Sutton等学者提出的公式计算表面张力[6-7]：

σdo=(1.11591-0.00305T)(38.085-0.259γAPI)

(3)

(4)

(5)

式中：σdo为气脱气原油表面张力，mN/m；γAPI为API重度；σlo为气含气原油表面张力，mN/m；Rs为溶解气油比，m3/m3。

(6)

式中：ρw为纯水密度，g/cm3；ρg为天然气密度，g/cm3；Cs为矿化度，mg/L；σhb为气水表面张力，mN/m。

3 井筒温压耦合计算模型

由于临界携液流量与温度、压力密切相关，因此需要准确预测井筒的温度和压力分布。考虑凝析气井中同时存在凝析油和地层水的情况，建立修正的拟单相流井筒温压耦合计算模型。

首先分析干气井井筒温度、压力分布，采用温压耦合方法计算[8-9]：

(7)

(8)

式中：v为气体流速，m/s；θ为井斜角，(°)；λc为摩阻系数；dti为油管内径，m；Te为地层温度，℃；Ar为松弛距离，1/m；qwax为井筒流体析蜡放出的熔解热，J/kg；cp为定压比热，J/(kg·℃)；η为焦耳-汤姆逊效应系数，℃/Pa；g为重力加速度，m/s2。

考虑井筒中为气体、凝析油和地层水三相，用如下方法进行参数修正[10]。

(1) 气体相对密度修正。地面单位体积的产出油、气、水总质量为：

(9)

式中：msum为地面产出油、气、水总质量，kg；Rl为生产气液比，m3/m3；γg为天然气相对密度；γo为地面凝析油的相对密度；γw为产出水的相对密度；fw为体积含水率。

地面产出油、气、水总物质的量为：

(10)

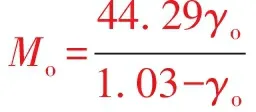
式中：nsum为地面产出油、气、水总物质的量，mol；Mo为凝析油平均相对分子质量；Mw为产出水平均相对分子质量。

复合气体的相对密度为：

(11)

(2) 气体流量修正。修正后的气体流量为：

(12)

式中：qmix为修正后气体流量，m3/d；qsc为标准状况下的气体流量，m3/d；qo为地面凝析油流量，m3/d；qw为地面产出水流量，m3/d。

进行凝析气井井筒温压计算时，首先利用式(11)、(12)对气体相对密度和流量进行修正，然后根据γmix计算复合气体的临界参数，确定偏差系数。参数修正后，根据式(7)、(8)进行耦合计算，即可得凝析气井的井筒温度、压力分布。

4 实例验证

雅克拉—大涝坝深层凝析气藏的物性参数如下：天然气相对密度为0.65～0.71，凝析油相对密度为0.77～0.80，地层水相对密度为1.07～1.17，井口油压为3～18 MPa。选用Hall-Varbongh方法计算天然气偏差系数[11]。

应用原始临界携液流量模型进行积液预测(杨川东模型需要利用井筒温压耦合模型计算井底条件下临界携液流量)，并与井筒流压梯度曲线得到的井筒实际积液情况进行比较，预测精度对比见表2。

表2 原始模型的预测精度对比

由表2可知，4种模型中李闽模型的预测结果精度最高，为76%，但是原始李闽模型的精度还有待进一步提高。其余3种方法能够准确预测积液井，但是预测非积液井时偏差很大，说明这3种方法的预测结果都比较保守。

应用文中改进模型，考虑沿井筒的临界携液流量最大值及表面张力的变化，再次进行积液预测，预测精度对比见表3。由表3可知，改进后的李闽模型预测结果精度最高，除一口井下入井下涡流工具导致积液预测结果不准外，其余井的预测结果与实际情况均相符，预测精度达到96%。

通过实例分析，改进的4种临界携液流量模型与原始模型相比均能够提高预测精度。其中，Turner、Coleman和杨川东模型精度提高幅度较小，李闽模型精度提高幅度较大，能够明显改善原始模型的预测精度。改进的李闽模型预测精度最高，适合于雅克拉—大涝坝深层凝析气井的积液预测。

表3 改进模型的预测精度对比

5 结 论

(1) 积液预测时应考虑临界携液流量沿井筒的差异分布，取井筒中的最大临界携液流量作为积液预测的判断标准。

(2) 表面张力影响临界携液流量准确性，应考虑表面张力沿井筒的差异分布，根据不同的温度、压力条件计算。

(3) 考虑井筒中为气体、凝析油和地层水三相，建立了凝析气井井筒温压耦合模型，为准确进行积液预测提供基础。

(4) 通过实例验证，改进的临界携液流量模型能够提高预测精度，改进的李闽模型积液预测精度最高，适合于雅克拉—大涝坝深层凝析气井的积液预测。

[1] 张大椿，刘晓，李远亮.凝析气藏井筒积液的诊断及排除方法综述[J].特种油气藏，2009， 16(3)：10-14.

[2] Duggan J O.Estimating flow rate required to keep gas wells unloaded[J].JPT，1961，13(12)：1173-1176.

[3] Turner R G，et al.Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells[J].JPT，1969，21(11)：1475-1482.

[4] 熊钰，等.两种准确预测低渗低产气井积液量的简易方法[J].特种油气藏，2015，22(2)：93-96.

[5] 刘双全，等. 气井井筒携液临界流速和流量的动态分布研究[J].天然气工业，2007，27(2)：104-106.

[6] Abdul-Majeed G H，Abu Al-Soof N B.Estimation of gas-oil surface tension[J] Journal of Petroleum Science and Engineering， 2000，27(3)：197-200.

[7] Sutton R P. An improved model for water-hydrocarbon surface tension at reservoir conditions[C].SPE124968，2009：1-18.

[8] 任瑛. 稠油与高凝油热力开采问题的理论与实践[M].北京：石油工业出版社，2001：5-8.

[9] 毛伟，梁政. 气井井筒压力、温度耦合分析[J].天然气工业，1999，19(6)：66-69.

[10] 杨继盛. 采气工艺基础[M].北京：石油工业出版社，1992：122-124.

[11] 廖锐全，曾庆恒，杨玲. 采气工程[M].北京：石油工业出版社，2012：7-8.

编辑 刘 巍

20150724；改回日期：20151009

国家科技重大专项“复杂结构井优化设计与控制关键技术”(2011ZX05009-005)；中国石油化工股份有限公司技术开发项目“深层凝析气井非常规排液采气工艺技术研究”(34400004-14-ZC0607-0001)

周朝(1988-)，男，2010年毕业于东北石油大学石油工程专业，现为中国石油大学(北京)油气田开发工程专业在读博士研究生，从事采油工程理论与技术研究工作。

10.3969/j.issn.1006-6535.2015.06.021

TE372

A

1006-6535(2015)06-0097-04