基于高斯混合模型的几何不变鲁棒水印算法

孟宪文

(中国人民公安大学公安情报研究中心， 北京　100038)

基于高斯混合模型的几何不变鲁棒水印算法

孟宪文

(中国人民公安大学公安情报研究中心， 北京100038)

摘要基于SIFT(scale-invariant feature transform)特征点和高斯混合模型(Gaussian mixture model)的几何不变鲁棒水印算法，对旋转、缩放、平移、仿射变换等几何攻击具有几何不变性。首先，用基于高斯混合模型的聚类算法对图像的所有SIFT特征点进行聚类。然后，逐比特地将水印信息嵌入到聚类后含有多个特征点的每个聚类中。因为水印信息的每个比特被嵌入到一个聚类的多个SIFT特征点中，因此水印的鲁棒性不再像传统的基于特征点的水印算法那样仅仅依靠单个特征点。使用两轮投票的策略从每个聚类中逐比特地提取出水印信息。实验结果表明，算法在抵抗多类几何变换攻击(如旋转、缩放、仿射变换、剪切等)和一般图像处理攻击(如JPEG压缩、图像滤波等)方面的鲁棒性要高于同类算法。

关键词鲁棒水印； 几何攻击； 高斯混合模型

0引言

网络化的多媒体系统的迅猛发展促使对数字多媒体文件(如图像、视频、音频等)的保护变得更加重要。版权保护主要解决非法拷贝和版权认证等问题。数字水印技术是解决该问题的一个有效途径。将数字签名等信息嵌入到多媒体文件中，用于声明版权和认证信息是数字水印技术的核心思想。在数字水印技术需要解决的诸多问题中，抵抗几何变化攻击是亟需解决的、最具挑战性的问题之一。

现今，抵抗几何攻击的鲁棒水印算法主要依靠以下关键技术：穷尽式搜索[1],RST不变域[2],RST不变矩[3-4],模板的使用[5],图像归一化[6],以及特征点和特征区域[7-10]。被称为第二代水印系统的基于特征点的水印系统在学术界引起了广泛的注意[11]。主要是因为基于特征点的方法可以为水印嵌者和提取者提供稳定的重同步的参考。这是水印系统抵抗几何攻击的有效方法。Bas等人用Harris角点检测的方法提取图像的特征点并用于水印的嵌入[7]。Tang和Hang等用MexicanHat小波变换来提取图像的特征点，然后在图像的DFT域的子块中进行水印的嵌入[8]。Lee等人首先提取SIFT特征点，然后根据SIFT特征点生成圆形的区域用于水印的嵌入[9]。Wang等人用Harris-Laplace检测子检测提取特征点，然后构建局部区域用于水印的嵌入[10]。对所有基于特征点的水印算法而言，其核心思想是将数字水印信息与特征点区域进行绑定。因此特征点的稳定是水印系统成败的关键[12]。本文看来，当前基于特征点的鲁棒水印算法主要有3个方面的不足：第一，水印信息或者叫水印的能量全都集中在特征点的周围，其他区域没有水印能量，因此水印系统的稳定性与特征点的稳定性密切相关。特征点的丢失或者破坏会带来水印系统的失败或者破坏；第二，水印的容量比较低，因为以特征点为位置标记的可用于水印嵌入的区域通常是面积比较小的局部区域，如果嵌入的水印比特数增加会导致水印鲁棒性的急剧减低；第三，可用于水印嵌入的特征点较小，一幅512×512的图像中，大概只有10个左右的特征点可用。如果有几个特征点在遭受攻击后丢失，将会严重损害水印的性能。

为解决基于特征点水印算法的上述缺点，本文提出了一种新的基于SIFT特征点和高斯混合模型的鲁棒水印算法。本文采用SIFT的方法提取图像的特征点。选用SIFT特征点的主要有两个原因。首先，SIFT特征点可以对旋转、缩放、平移、仿射变换等几何变换提供非常好的稳定性[13]。另外，SIFT的方法可以产生较多的SIFT特征点，这些特征点密集地分布于图像的不同尺度和不同位置上[13]。在本文的算法中，提取出SIFT特征点后，我们用高斯混合模型对所有的SIFT特征点进行聚类。聚类分组的个数就是要嵌入水印信息的长度即水印序列的长度。每一个聚类中嵌入1比特水印。由于采用了所有的、密集的SIFT特征点的聚类，水印系统的鲁棒性就不仅仅受限于几个特征点的稳定性。因此，本文所提出的水印算法对几何攻击具有较好的鲁棒性。

1SIFT特征点和高斯混合模型(GMM)

1.1　尺度不变特征变换(SIFT)特征点

SIFT是从图像中提取具有差异性的不变特征的方法。该方法可用于物体或场景的变换时图像点的稳定特征匹配等应用中。SIFT特征点具有较好的图像缩放、旋转不变性，并且对仿射变换、3D投影变换、噪声、光照强度等变换也具有较好的鲁棒性[13]。SIFT算法主要有四个步骤[13]：(1)尺度空间峰值点的选择；(2)特征点的定位；(3)方向的分配；(4)SIFT描述子的生成。该算法会提取SIFT特征点的4类特征，它们是：特征点的位置(t1,t2)、尺度s、方向θ以及128维的向量ds(被命名为SIFT描述子)。其中，尺度s可以随图像的缩放等比例变换；方向θ也随着图像的旋转而变换；SIFT描述子ds具有旋转、缩放、平移、仿射变换不变性。

1.2　高斯混合模型

高斯混合模型(Gaussian Mixture Model，GMM)是参数化的概率密度函数，用高斯分量密度加权和来表示。高斯混合模型的参数可以利用迭代的最大期望值(Expectation-Maximization，EM)算法从训练数据中得到。

一个高斯混合模型由M个成分的高斯分布加权组成，如下式所示，

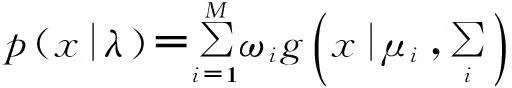
(1)

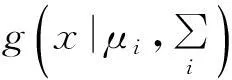
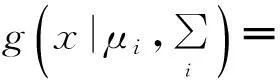
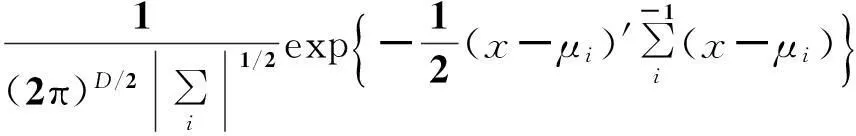
(2)

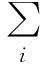
完整的高斯混合模型可以用各个成分概率分布密度的均值向量、协方差矩阵和混合权重来参数化地表示。这些参数可以用下述符号统一表示：

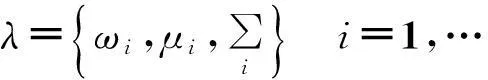
(3)

给定一个训练向量和一个高斯混合模型的结构，便可以估计出高斯混合模型的参数λ。估计高斯混合模型的参数有很多种[14]。现在，最大似然估计法(maximum likelihood，ML)是最流行同时也是最稳定的。最大似然估计的目的是找到模型的参数使得高斯混合模型的似然函数最大化。对T个训练向量组成的序列X={x1,…,xT},高斯混合模型的似然函数可以写为：

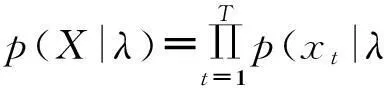
(4)

最大似然的参数估计可以通过最大期望值迭代的方法得到[15]。

2本文的鲁棒水印算法

2.1　水印的嵌入算法

图1为本文鲁棒水印算法的水印嵌入流程图。水印的嵌入过程有如下4个主要步骤。

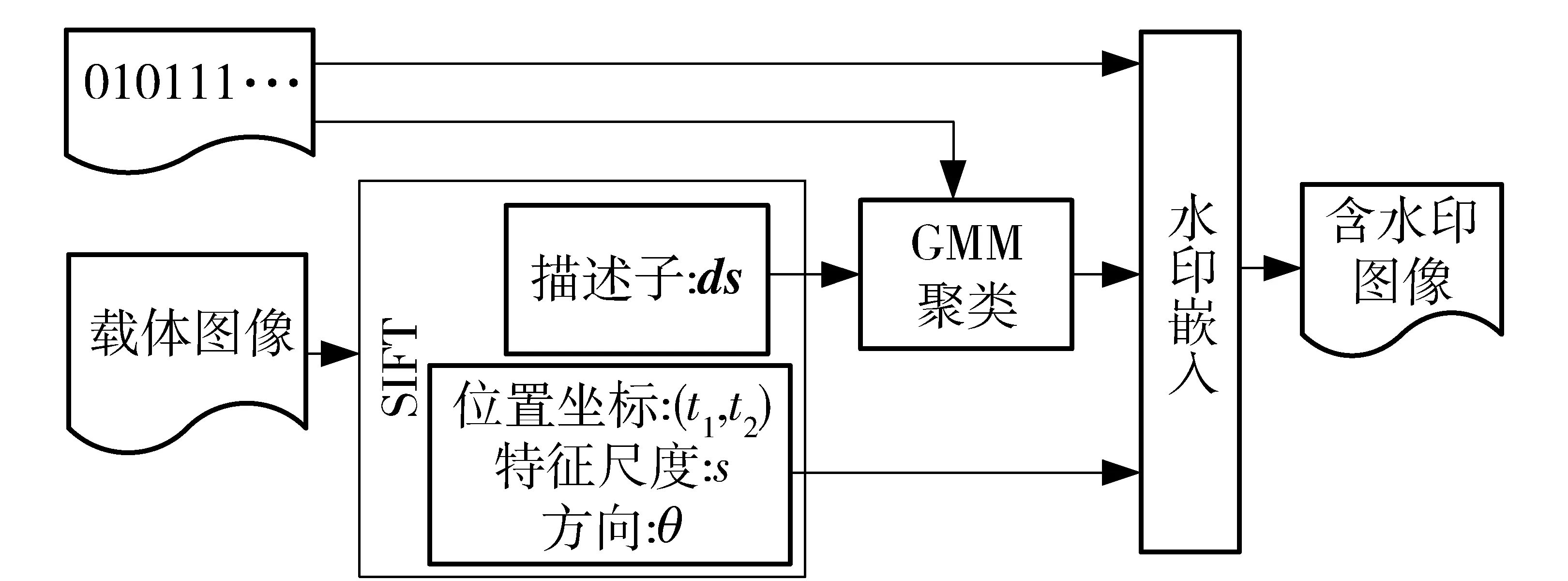
图1　水印嵌入算法流程图　

步骤1提取载体图像的SIFT特征。利用SIFT特征变换提取载体图像的SIFT特征点，并得到每个SIFT特征点的特征描述子ds，位置(t1,t2)，尺度s，方向θ。

步骤2利用高斯混合模型，根据SIFT特征点的特征描述子ds对所有SIFT特征点进行聚类，将其划分为k(这里k为水印序列的长度)个聚类。

步骤3将水印信息序列逐比特地嵌入到每一个聚类中，每个聚类中嵌入一个水印的比特。具体而言，每个聚类内的所有SIFT特征点都含有相同的水印比特。

在步骤3中，本文用量化索引调制(Quantization Index Modulation，QIM)[16]的方法嵌入水印的比特流。对水印信息序列W=(w0w1…wi…wk),这里wi∈{0,1}，本文方法在一个聚类Ci中只嵌入一个水印比特wi。如图2所示，SIFT圆形特征区域以像素P为中心，其坐标为(ti1,ti2)。这个坐标同时也是SIFT特征点xij的坐标。圆形区域的半径为R，设定其值与SIFT特征点xij的特征尺度si相等，这里xij∈Ci。直线L的方向代表SIFT特征点xij的特征方向θi。直线K为直线L的垂线，它将圆形区域划分为两个半圆区域Ω和Ψ。因为SIFT特征点xij的特征尺度si会随着图像的放大缩小同比例变化，特征方向θi会随着图像的旋转而变化，因此不论图像如何旋转和缩放，半圆区域Ω和Ψ所覆盖的内容都不会发生变化。

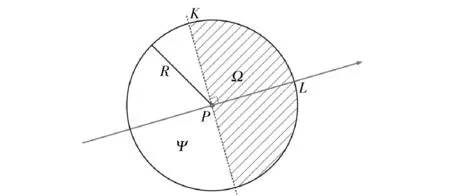
图2　SIFT圆形区域的划分　

根据待嵌入水印比特wi，由vi1和vi2构成的向量vi=[vi1vi2]将被分别嵌入到半圆形区域Ω和Ψ的所有像素点中。如果wi=0，那么将vi1=0和vi2=1用QIM (Quantization Index Modulation)[16]方法分别嵌入到半圆形区域Ω和Ψ的所有像素点中。如果wi=1，那么将vi1=1和vi2=0用QIM方法分别嵌入到半圆形区域Ω和Ψ的所有像素点中。根据待嵌入比特w∈{0,1}，QIM构建两个量化器Q(.；w)。对半圆形区域Ω和Ψ而言，根据对应需要嵌入的比特vij，对每个像素p(m,n)用QIM的量化器进行量化：

pw(m,n)=Q(p(m,n);vij)

(5)

这里，vij∈{0,1}，j∈{1,2}。

2.2　水印的提取算法

如图3所示，数字水印检测算法由3个主要步骤组成：

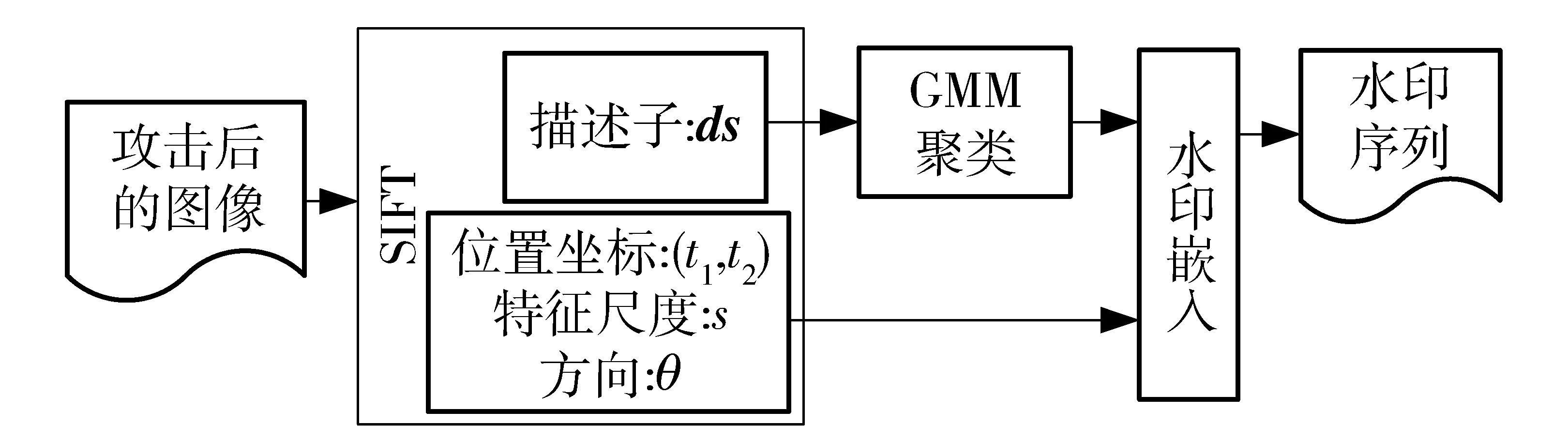
图3　水印提取流程图　

步骤1从被攻击图像中提取SIFT特征，包括SIFT特征点的特征描述子ds、位置(t1,t2)、尺度s、方向θ等信息。

步骤2根据每个SIFT特征点的特征描述子ds，将所有的SIFT特征点x用高斯混合模型聚类到k个聚类中，这里k是水印序列的长度。

步骤3利用两轮投票的策略，从每个聚类中逐比特地提取出水印序列。

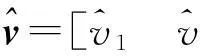
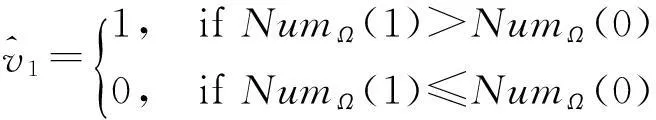
(6)

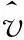
第二轮投票：对聚类Ci的每个SIFT特征点xij，根据第一轮投票的结果令Numi(1)和Numi(0)分别表示在聚类Ci内，SIFT特征点周围检测出的比特“1”和比特“0”的个数。那么从聚类Ci中提取出的水印序列的第i个比特的值为：

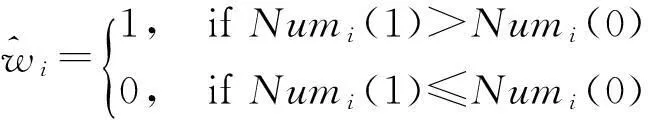
(7)

3实验结果和比较

本文用20幅不同纹理的、大小为512×512像素的图像作为测试图像来验证数字水印算法的鲁棒性和不可见性。为了和文献[12]中的数字水印方法做比较，在每幅图像中我们将长度为50比特的水印序列嵌入到由SIFT特征点构成的50个聚类中。

本文用PSNR(峰值信噪比)值来衡量水印算法的不可见性，实验结果如图4所示。从图4可以观察，含水印的图像与原始图像的PSNR值都分布在36dB到42dB之间。因此，本文的数字水印算法具有较好的不可见性。图5和图6分别展示了本文水印算法的对旋转和缩放攻击的鲁棒性，同时图上还展示了与文献[12]算法的比较结果。从图5和图6可以看出，本文水印算法的比特错误率(BER)要低于文献[12]算法的比特错误率，隐藏本文水印算法的鲁棒性在抵抗旋转和缩放攻击方面要优于文献[12]的算法。图7显示了本文水印算法在抵抗StirMark3.1攻击[17]时的鲁棒性。StirMark3.1是一种国际公认的对水印鲁棒性进行测试的攻击标准，包括一系列的一般图像处理攻击和几何攻击。图7中的15种攻击具体包括：中值滤波攻击2×2和3×3、高斯滤波3×3、JPEG压缩(系数分别为90、60和40)、随机删除5行17、中心剪切10%、Shearing变换(1%，1%)、Shearing变换(0%，5%)、Shearing变换(5%，5%)、线性几何变换(1.007，0.01，0.01，1.012)、线性几何变换(1.010，0.013，0.009，1.011)、线性几何变换(1.013，0.008，0.011，1.008)以及随机扭曲变换攻击(Randbendattack)。如图7所示，在抵抗StirMark3.1系列攻击方面本文水印算法的鲁棒性也要高于文献[17]的水印算法。

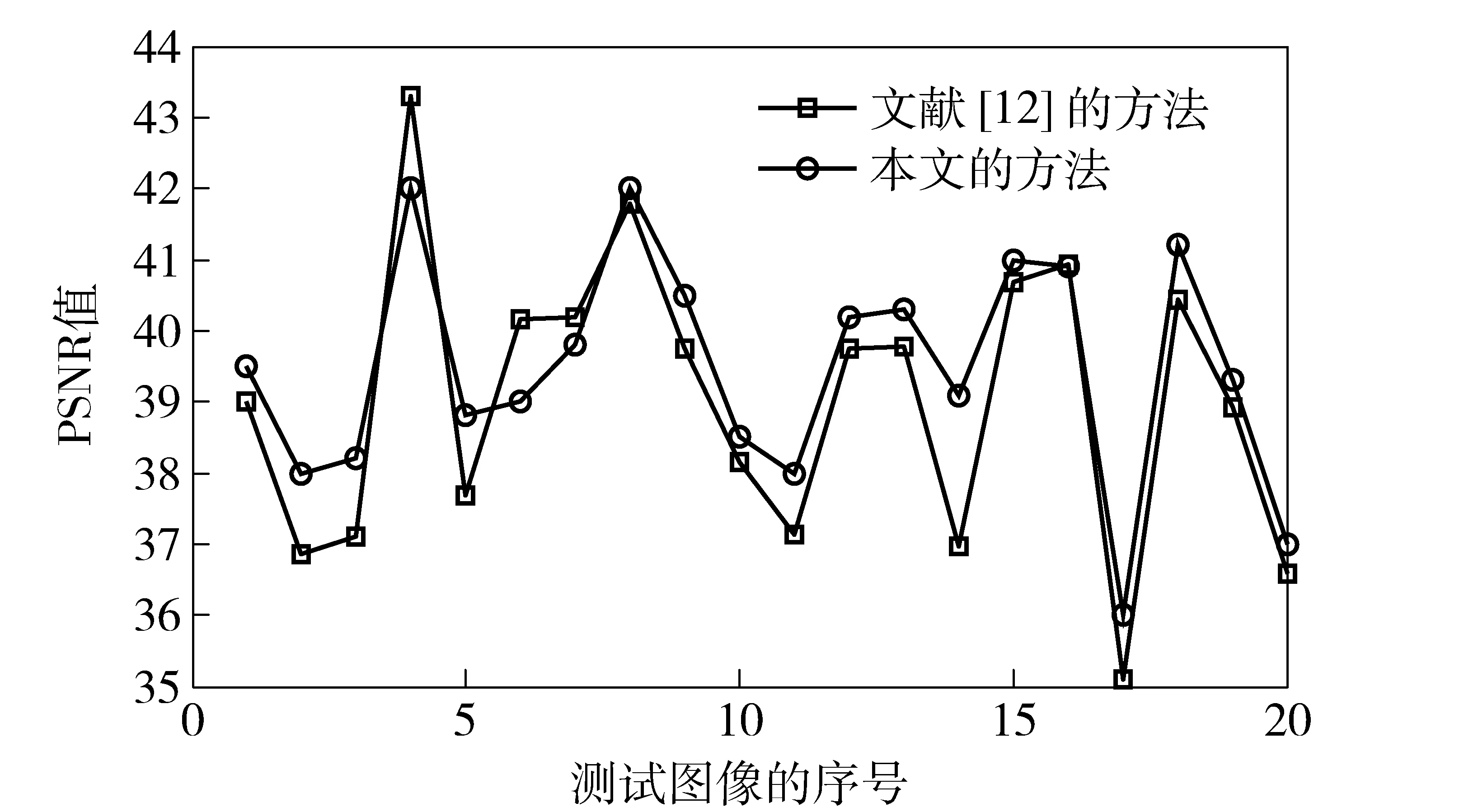
图4　水印带来的图像的损失(用PSNR值度量)　

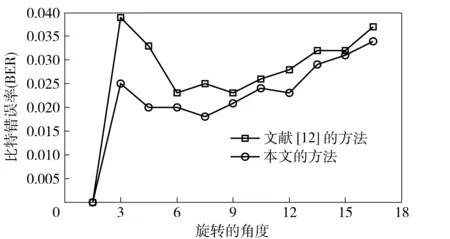
图5　抵抗旋转攻击的鲁棒性　

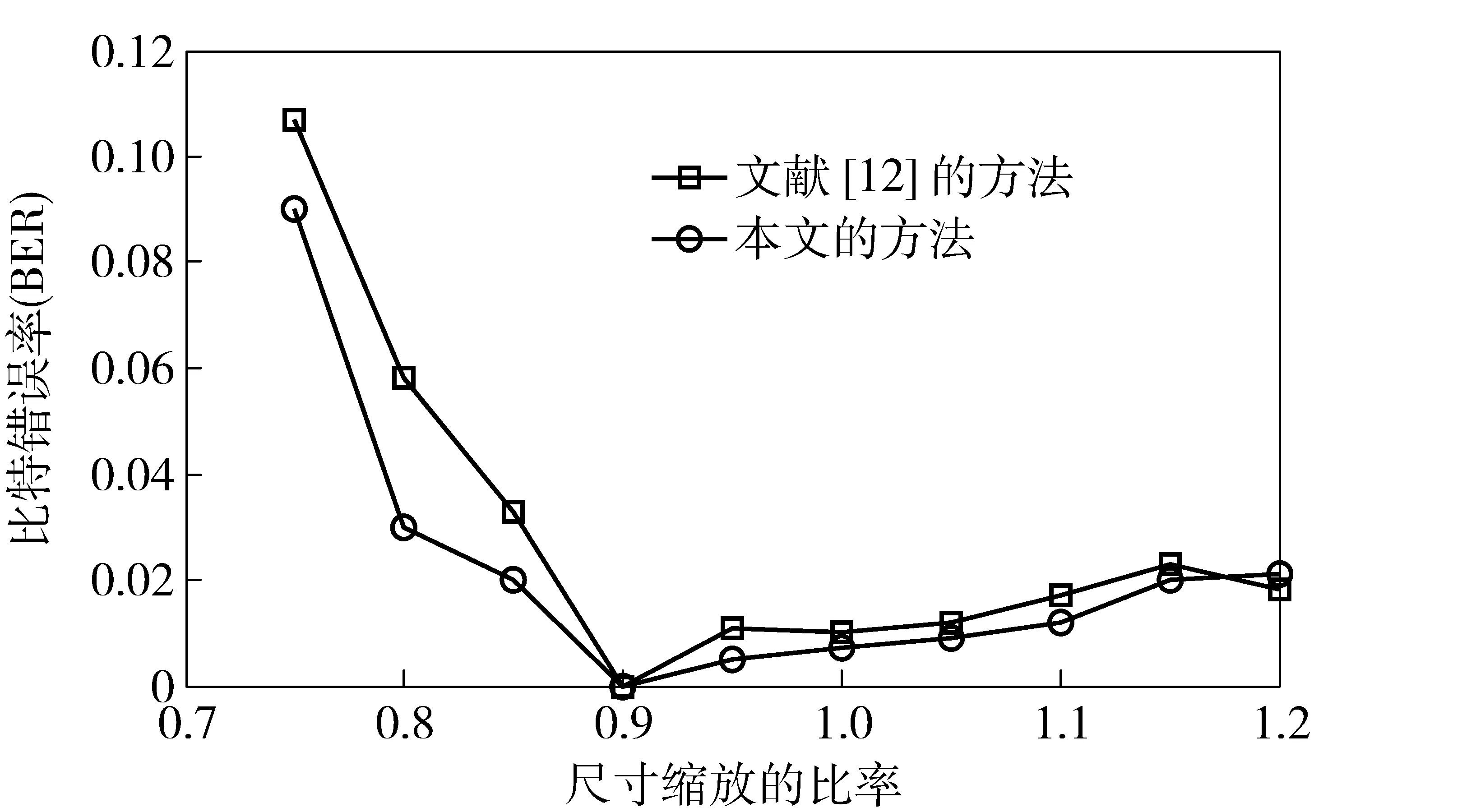
图6　抵抗尺寸缩放攻击的鲁棒性　

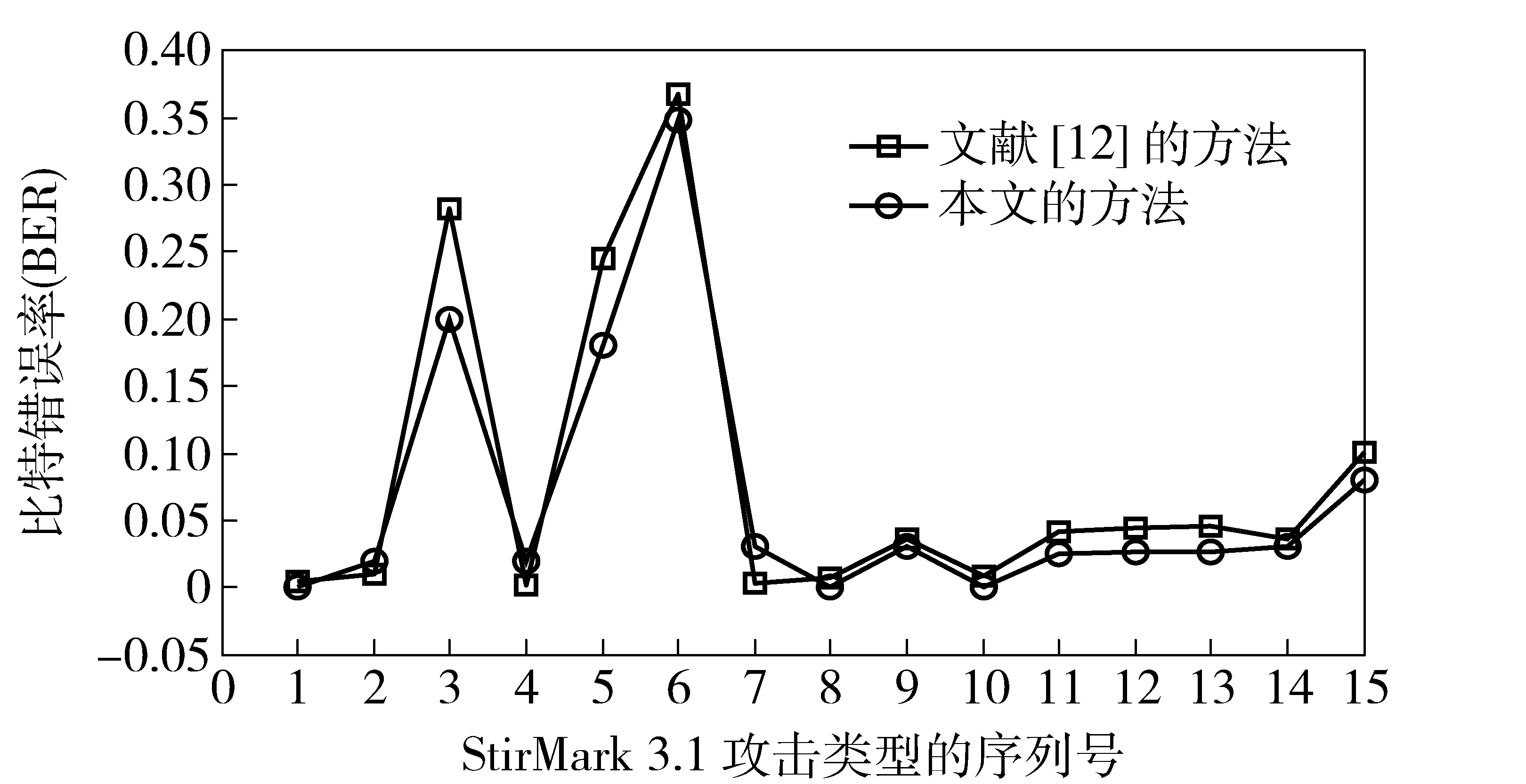
图7　抵抗StirMark 3.1攻击的鲁棒性　

4结语

为抵抗几何攻击和一般图像处理攻击并克服传统基于特征点的鲁棒水印方法的不足，本文提出了一种基于SIFT和高斯混合模型的鲁棒水印算法。该算法首先提取出SIFT特征点，然后利用高斯混合模型对所有的SIFT特征点进行聚类。聚类分组的个数就是要嵌入水印信息的长度即水印序列的长度。每一个聚类中嵌入1比特水印。由于采用了所有的、密集的SIFT特征点的聚类，水印系统的鲁棒性就不仅仅受限于几个特征点的稳定性。实验结果证明，该算法在保持较好的不可见性的同时可以有效抵抗几何攻击(包括旋转、缩放、Shearing变换、线性几何变换等)和一般图像处理攻击(包括中值滤波、高斯滤波、JPEG压缩等)，并且该算法的鲁棒性要优于已有的该类水印算法。

参考文献

[1]BARNI M. Effectiveness of exhaustive search ant template matching against watermark desynchronization[J]. IEEE Signal Process. Lett., 2005,12(2):158-161.

[2]RUANAIDH J J, PUN T. Rotation, scale and translation invariant spread spectrum digital image watermarking[J]. Signal Process., 1998,66(3):303-317.

[3]ALGHONIEMY M, TEWFIK A. Image watermarking by moment invariants[C]∥Image Processing, 2000. Proceedings. 2000 Intemational Conference on. IEEE, 2000,2:73-76.

[4]XIN Y, LIAO S, PAWLAK M. Circularly orthogonal moments for geometrically robust image watermarking[J]. Pattern Recognit., 2007,40(12):3740-3752.

[5]PEREIRA S, PUN T. An iterative template matching algorithm using the Chirp-Z transform for digital image watermarking[J]. Pattern Recognit., 2000,33(1):173-175.

[6]DONG P, BRANKOV J G, GALATSANOS N P, et al. Digital watermarking robust to geometric distortions[J]. IEEE Trans. Image Process., 2005,14(12):2140-2150.

[7]BAS P, CHASSERY J, MACQ B. Geometrically invariant watermarking using feature points[J]. IEEE Trans. Image Processing, 2002,11(9):1014-1028.

[8]TANG C, HANG H. A feature-based robust digital image watermarking scheme[J]. IEEE Trans. Image Processing, 2003,51(4):950-959.

[9]LEE H Y, KIM H, LEE H K. Robust image watermarking using local invariant features[J]. Optical Engineering, 2006,45(3):037002-037002-11.

[10]WANG X, WU J, NIU P. A new digital image watermarking algorithm resilient to desynchronization attacks[J]. IEEE Trans. Information Forensics and Security, 2007,2(4):655-663.

[11]TIAN H, ZHAO Y, NI R, et al. LDFT-Based Watermarking Resilient to Local Desynchronization Attacks[J]. IEEE Trans. Cybernetics, 2013,43(6):2190-2201.

[12]TIAN H, ZHAO Y, NI R, et al. Geometrically Invariant Image Watermarking Using Scale-Invariant Feature Transform and K-Means Clustering[M]∥Computational Collective Intelligence. Technologies and Applications. Springer Berlin Heidelberg, 2010:128-135.

[13]LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004,60(2):91-110.

[14]MCLACHLAN G J, BASFORD K E. Mixture models: Inference and applications to clustering[J]. Applied Statistics, 1988.

[15]DEMPSTER A, LAIRD N, RUBIN D. Maximum Likelihood from Incomplete Data via the EM Algorithm[J]. Journal of the Royal Statistical Society. Series B(Methodological), 1977:1-38.

[16]CHEN B, WORNELL G W. Preprocessed and postprocessed quantization index modulation methods for digital watermarking[C]∥Electronic Imaging. International Society for Optics and Photonics, 2000:48-59.

[17]PETITCOLAS F A P, ANDERSON R J, KUHN M G. Attacks on copyright marking systems[C]∥Information Hiding. Springer Berlin Heidelberg, 1998:218-238.

(责任编辑陈小明)

作者简介孟宪文(1956—)，男，山东济南人，教授。研究方向为公安情报技术。

基金项目国家自然科学基金项目(61402484)。

中图分类号D918.9