基于综合结构势概念的结构性原状黄土屈服准则

钟祖良 ，王 睢，刘新荣

（1.重庆大学 土木工程学院，重庆 400045；2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045）

1 引 言

目前关于土的破坏条件和屈服准则已有几十种甚至上百种[1-2]，对于黄土本构关系的研究也有很多种，而对于黄土来讲人们最关心的是它的结构性对其应力-应变关系的影响，杨光华[3]在 Mohr-Coubomb（M-C）准则及D-P 准则基础上，提出一个在π 平面上不存在角点的符合于实际的改进型岩体屈服准则；邢义川等[4]基于黄土破坏特性提出了一个新的破坏条件，该条件在P-Q 平面上仍采用Mohr-Coubomb（M-C）条件，并根据黄土试验资料对几种典型破坏条件进行了评述，得到了良好的吻合度，可以供黄土的计算所采用。Xiao 等[5]通过结合Matsuoka-Nakai 破坏准则和Lade-Duncan 破坏准则推导出一个新的强度破坏准则，该准则能够较好地模拟土体的各向异性。谢定义[6]将所提出的土结构性定量化参数引入土的变形本构关系和强度本构关系，得到了以结构性参数为基础来描述土的变形和强度的基本规律的本构关系，使土力学特性的研究迈入了新的台阶，也为今后的研究指引了正确的方向。陈存礼等[7]将三轴应力条件试验下得到定量化结构性参数，将结构性应力-应变曲线采用邓肯-张模型来模拟，用来描述软化型和硬化型的应力-应变关系。Liu 等[8]基于扰动土概念，通过3 个基本假定，建立了结构性岩土材料的各向同性压缩模型。该模型能够对各种结构性岩土材料的力学特性进行较好的模拟，例如，黏土、砂土、软岩等。刘恩龙等[9]基于岩土二元介质模型思想通过引入随应力状态变化的剪切抗力贡献率参数，建立了结构性土的强度准则，并对准则中参数的变化对强度规律的影响进行了分析。最后与结构性土的真三轴和常规三轴试验结果进行了对比，表明其强度准则具有较好的适用性。邓国华等[10]将结构性参数引入到修正剑桥模型中来预测结构性土的力学特性，并验证提出的模型能比较准确地反映结构性土的强度变形规律。殷杰[11]建立了考虑结构性的天然软黏土的修正剑桥模型，并引入结构屈服应力参数表征受土结构性影响的天然土初始屈服面的形状，引入各向异性参数描述天然土体初始各向异性引起的屈服面旋转，建立了适用于结构性软黏土的弹塑性本构模型。随着西部大开发战略的实施，在基础设施工程建设中遇到越来越多的黄土工程。为了确保工程的安全顺利实施，必须对黄土的力学性质进行正确认知。而结构性对黄土的力学特性和本构模型的影响显著，因此，对结构性黄土的破坏准则的研究必须考虑其结构性。

基于上述前人研究成果可知，对于黄土的屈服准则和本构模型的研究大都基于摩尔-库仑准则进行修正的，摩尔-库仑准则最大的优点是它既能反映岩土类材料的抗压强度不同的S-D 效应与净水压力的敏感性，而且简单实用，但是摩尔-库仑准则在π平面内的屈服面有棱角，不便于塑性应变增量的计算，给数值计算带来了困难[12]。基于上述问题，本文采用无棱角的D-P 屈服准则进行修正，既克服了无棱角的缺陷又同时考虑了结构性的影响，可以很好地反映Q2原状黄土的力学特性。

2 Q2原状黄土的屈服准则

要研究材料的塑性本构关系和塑性极限荷载，必须建立材料产生屈服与破坏的条件与准则。目前，岩土材料的屈服准则有很多种，也有很多学者根据岩土体的实际试验资料进行了修正。D-P 准则既考虑了静水压力的影响，也克服了M-C 准则的棱角，有利于进行数值计算，所以在数值分析中经常采用D-P 屈服准则。本文根据经典D-P 屈服准则进行修正，推导出适合Q2原状黄土的屈服准则。D-P 屈服准则的表达式可表示为[13]

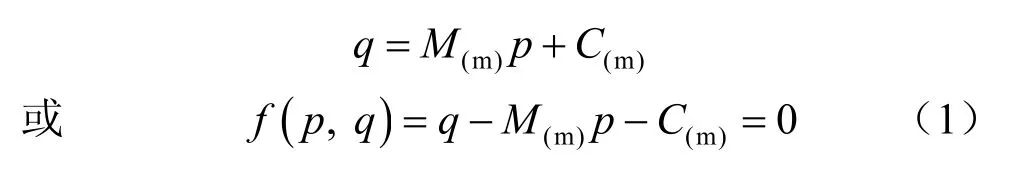
式中：q为偏应力；p为球应力；f（p,q ）为屈服面函数；M(m)为关于摩擦角的系数，M(m)=C(m)为关于摩擦角和黏聚力的系数，，其中，φ(m)为摩擦角与结构性参数的拟合函数关系式，c(m)为黏聚力与结构性参数的拟合函数关系式。

为了研究上述问题，试验所用的土样取自山西省离石至临县高速公路姚家山黄土隧道内埋深为45 m 处的上台阶中部，该处土体为第四系中更新世离石组黄土（Q2）。利用非饱和三轴压缩仪对不同含水率w（15.00%、17.09%（天然含水率）、19.00%和21.58%（饱和含水率））的非饱和Q2黄土的原状样、重塑样进行三轴压缩试验。土样在给定的固结压力下固结24 h 后，分别在50，100，200，300 kPa的围压下进行固结不排水三轴剪切试验（CU 试验）并获得了相应力-应变关系曲线[14]。

结构性参数m 定义为

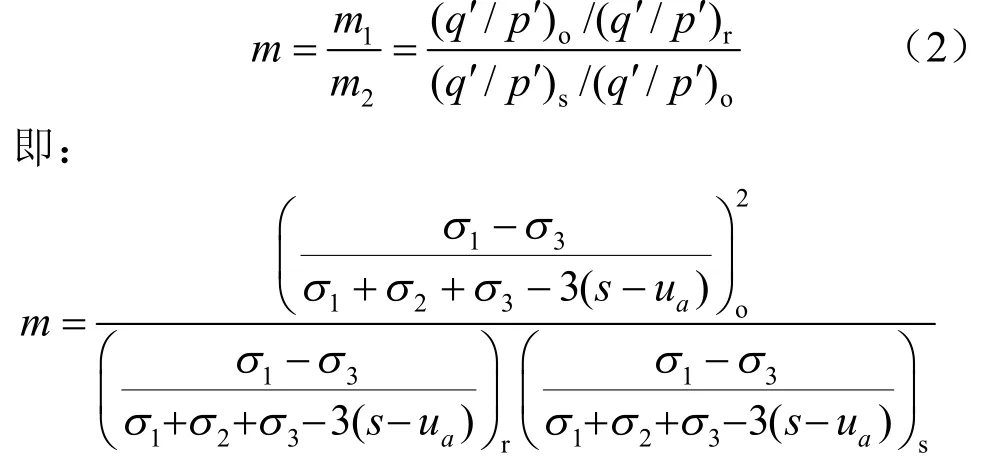
式中：m为应力比结构性参数；m1为反映结构可稳性参数；m2为反映结构可变性参数；(q′/p′)o为饱和土在剪切过程中考虑基质吸力下的应力比；(q′/p′)r为重塑土在剪切过程中考虑基质吸力下的应力比；(q′/p′)s为原状土在剪切过程中考虑基质吸力下的应力比。

由式（1）、（2），并结合Q2黄土三轴压缩试验结果可计算出不同围压和含水率条件下的结构性参数m，其变化规律如图1 所示。

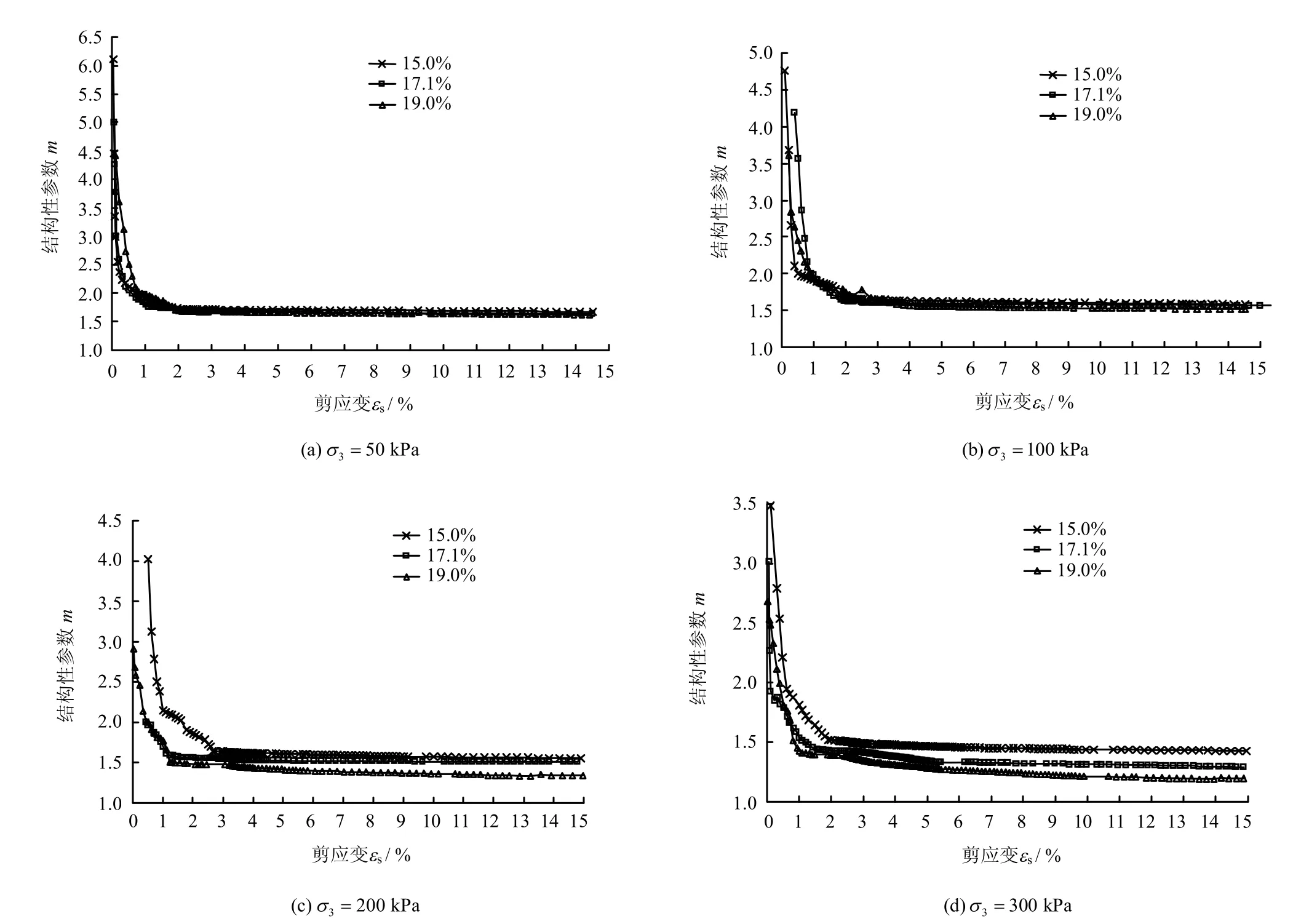
图1 不同围压和含水率条件下结构性参数m 与剪应变εs的关系曲线Fig.1 Relationships between structural parameter m and shear strain εsfor different confining pressures and moisture contents

由图1 可知，在相同含水率条件下，随着剪应变的增大，结构性参数减小；在相同剪应变下含水率越大，其结构性参数越小。由于剪切作用使土的结构发生了显著变化，原状土的胶结强度由于剪切位移的产生而显著减弱，土颗粒的空间不稳定作用力系统逐渐向稳定状态过渡。

由试验数据可计算得出结构性参数与黏聚力c、摩擦角φ 的对应关系如表1 所示。

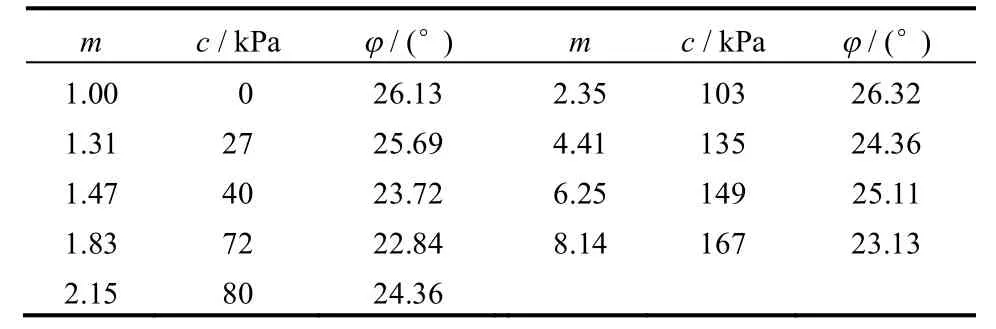
表1 m 和c,φ 的对应关系Table 1 m and its corresponding relation with c and φ

利用线性回归方程拟合c 与m 的关系曲线方程为c(m)=14.473 9 +77.549lnm，取显著水平α=0.05，用r 检验法进行检验得：

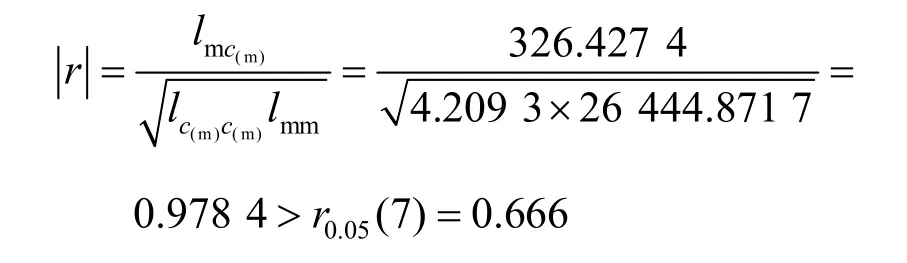
因此，c(m)与ln m 的线性关系显著，可以用 c(m)表达式表示c 与m 的关系。

利用线性回归方程拟合φ 与m 的关系曲线方程为φ(m)=25.193 8-0.174 98m，取显著水平α=0.05，用r 检验法进行检验得：

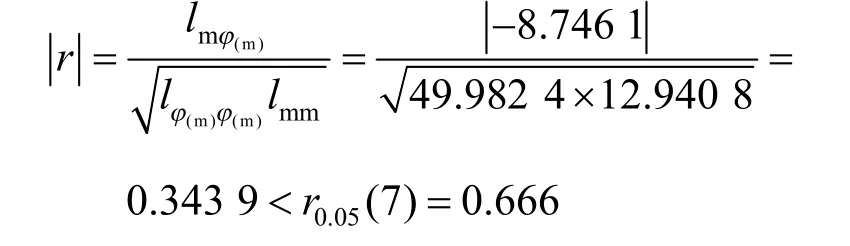
φ 与m 的关系拟合误差较大，因此，函数关系不显著。说明结构性参数的变化对摩擦角影响小，已有文献[8]证明其没有固定的关系。本文φ 取试验平均值φ=24.63°。

3 Q2原状黄土的屈服面方程

3.1 Q2原状黄土的能量方程及相关假定

在塑性力学增量理论中岩土体在受到外力作用时会产生相应的体积应变εv和剪切应变 γs，将体积应变和剪切应变分解为弹性部分和塑性部分单位体积土在八面体应力和状态下，加载时由偏应力增量q 和球应力增量p 产生的有体积应变增量dεv和剪切应变增量dγs，则可以表示为[15]

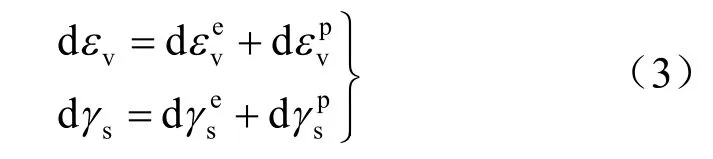
根据变形能增量可以分解为弹性应变能增量和塑性应变能增量，即：

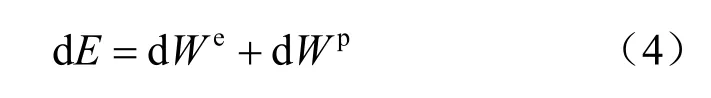
式中：We为弹性应变能；Wp为塑性应变能，两者可以表示为

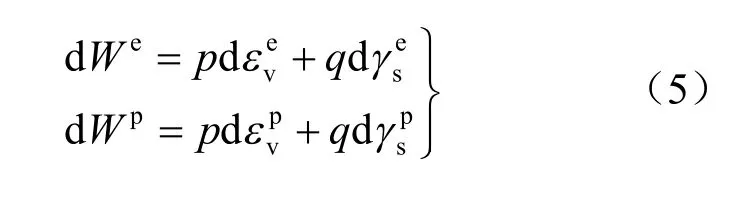
将式（5）代入式（4）可以得到外力所做的功可表示为

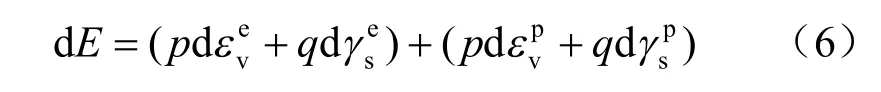
根据上式整理可得：

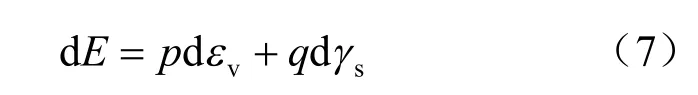
由上述假设可得[15]：

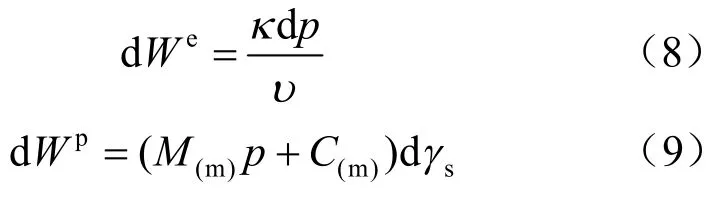
式中：υ为比容，表示单位体积颗粒与孔隙体积之和，即υ=1+e（e为孔隙比）；κ为等向再压缩曲线OCL 线的斜率。

本文推导的屈服准则将这υ、κ 作为求解过程的过渡参数。

可确定能量方程为

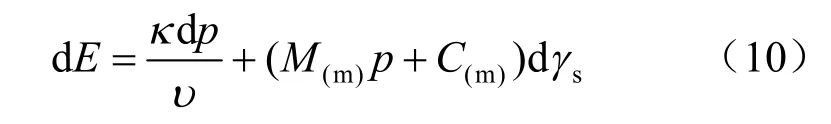
整理后可得：

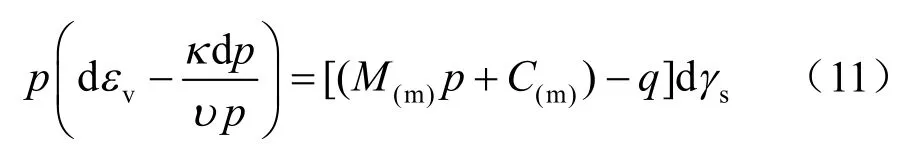
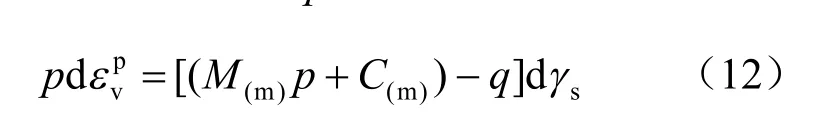
由于dγs=dγsp，故式（12）可表示为

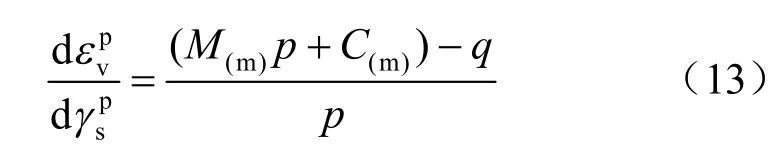
3.2 屈服面方程

3.2.1 流动法则

流动法则使塑性变形增量中的不同塑性应变率与引起这些塑性变形的应力状态建立关系，而塑性屈服面是将只引起弹性应变的应力状态与同时引起塑性和弹性两种应变的应力状态区别开来。流动法则使塑性应变增量矢量的方向与屈服面建立关系[13]，对于Q2黄土符合流动法则，其表达式为

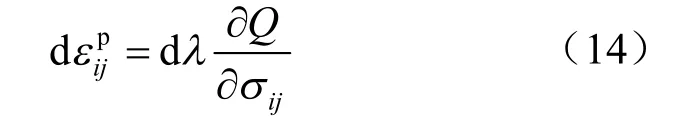
式中：dλ为非负的塑性标量因子，表示塑性应变增量的大小；Q为塑性势函数。将流动法则公式分解为体积流动法则和剪切流动法则时可得：

根据文献[15]推导剑桥模型时的相关假定，假设Q2黄土材料服从流动法则，可知Q=f=φ，流动法则可表示为

3.2.2 硬化规律

加载面在应力空间中的位置、大小和形状的变化规律称为硬化规律[15]。可见硬化规律与加载函数有关，对于硬化模型通常表示为

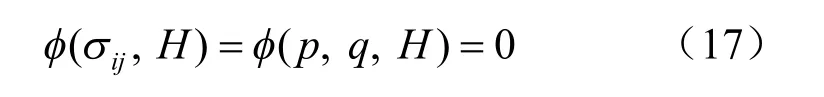
式中：H为硬化函数，根据相关假定可知，Q=f=φ，故屈服面方程可以表示为

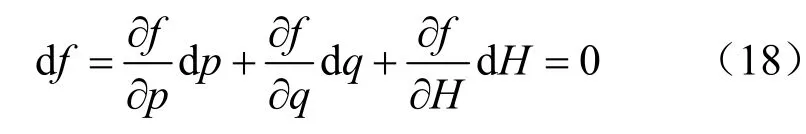
在同一屈服面上硬化参数为常数，即dH=0，则可以得到：

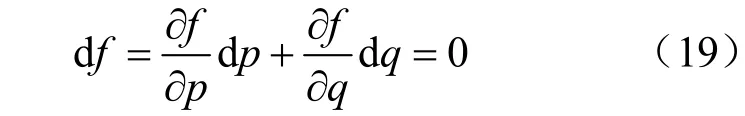
将流动法则代入上述硬化准则可得：

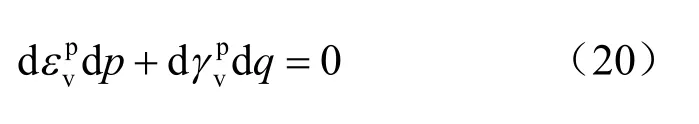
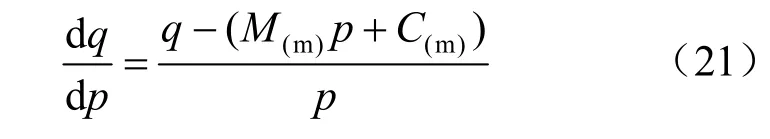
求解上述微分方程可得：

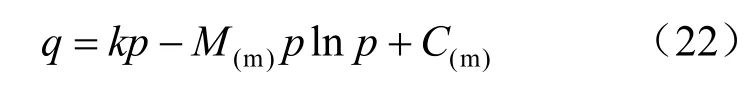
式中：k为积分常数。

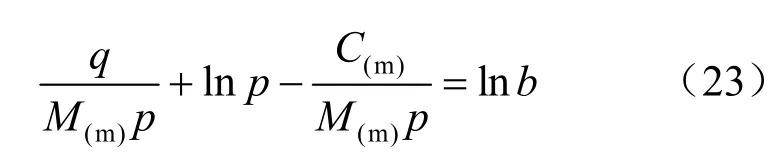
因此，就可以得到考虑结构性参数的屈服面方程。如果加载路径经过原始各向等压固结线上一点(p0,0,e0)时，积分常数取b=p0，其屈服面轨迹方程可写为

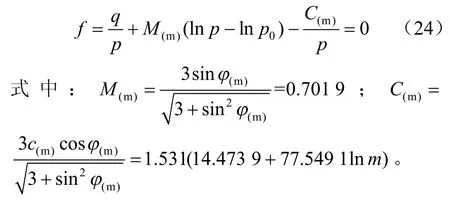
式（24）可表示为

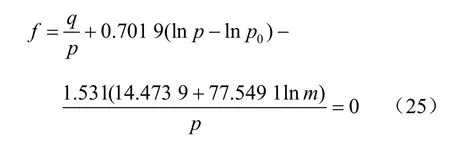
分别取p、q 和m为坐标轴，屈服面形状如图2所示。

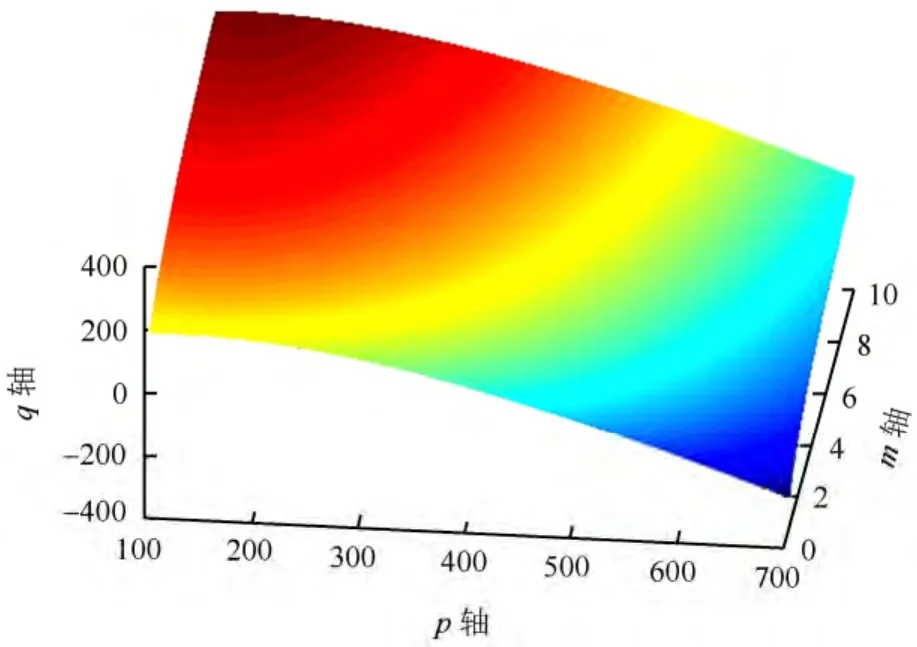
图2 考虑结构性的屈服面形状Fig.2 Shape of yield surface considering structure

从图中可以看出，结构性参数m 对屈服面的影响。此外，该图形符合屈服面的形状，为盖帽模型屈服轨迹的一部分，如果加上临界状态线即为完整的剑桥模型的双屈服面轨迹。

3.3 屈服面模型验证

为了验证上述屈服轨迹方程的正确性，本文分别选取结构性参数m=2.115、4.408、8.114 时分别计算并作出3 组屈服轨迹，与试验数据值对比，其结果见图3。

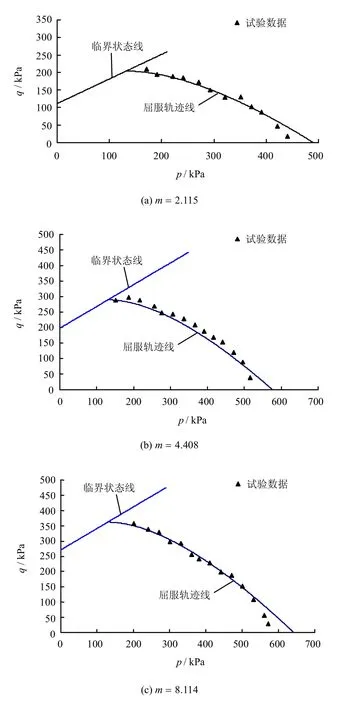
图3 不同m 值下屈服面计算轨迹与试验数值对比Fig.3 Comparisons between calculated yield surface track and experimental values at different values of m

从图可知：结构性对黄土的力学特性影响显著，结构性参数越大，其屈服应力越大。此外，由计算获得的屈服面轨迹与试验数值吻合地较好，从而验证了本文推导的屈服面轨迹方程的正确性。

4 结 论

（1）本文定义了可考虑球应力、偏应力和基质吸力等因素的土的结构性参数m，并通过对非饱和Q2原状黄土三轴试验数据进行计算，获得了结构性参数与黏聚力和摩擦角的关系，推导了相应的曲线方程。研究表明，结构性参数m 与黏聚力c 线性关系显著，而与摩擦角φ 关系不显著。

（2）结合结构性参数与黏聚力和摩擦角的关系方程，分别将曲线方程代入到D-P 准则方程中并对其进行修正，建立了可以考虑结构性参数m 的原状黄土的屈服面方程。通过对计算的屈服面轨迹与试验数值进行对比，获得了良好的吻合性，验证了本文推导的结构性黄土屈服方程的正确性，为建立考虑结构性影响的原状黄土本构模型提供理论基础。

[1]孔亮,郑颖人,王燕昌.一个基于广义塑性力学的土体三屈服面模型[J].岩土力学,2000,21(2):108－111.KONG Liang,ZHENG Ying-ren,WANG Yan-chang.A three-yield-surface model for soil masses based on the generalized plastic mechanics[J].Rock and Soil Mechanics,2000,21(2):108－111.

[2]冶小平,孙强,王媛媛,等.一种改进的黏土亚塑性本构模型[J].岩土力学,2010,31(4):1099－1102,1107.YE Xiao-ping,SUN Qiang,WANG Yuan-yuan,et al.A modified hypoplastic constitutive model for clay[J].Rock and Soil Mechanics,2010,31(4):1099－1102,1107.

[3]杨光华.一个可改进的岩体屈服准则[J].武汉水利电力学院学报,1985,(2):112－117.YANG Guang-hua.A modified criterion for rock mechanics[J].Journal of Wuhan University of Hydraulic and Electric Engineering,1985,(2):112－117.

[4]邢义川,刘祖典,郑颖人.黄土的破坏条件[J].水利学报,1992,(1):12－19.XING Yi-chuan,LIU Zu-dian,ZHENG Ying-ren.A failure criterion of loess[J].Journal of Hydraulic Engineering,1992,(1):12－19.

[5]XIAO Yang,LIU Han-long,YANG Gui.A united anisotropic strength criterion for soils[J].Geotechnical Special Publication,2011:23－31.

[6]谢定义,齐吉琳,张振中.考虑土结构性的本构关系[J].土木工程学报,2000,33(4):35－41.XIE Ding-yi,QI Ji-lin,ZHANG Zhen-zhong,A constitutive laws considering soil structural properties[J].China Civil Engineering Journal,2000,33(4):35－41.

[7]陈存礼,何军芳,杨鹏.考虑结构性影响的原状黄土本构关系[J].岩土力学,2007,28(11):2284－2290.CHEN Cun-li,HE Jun-fang,YANG Peng.Constitutive relationship of intact loess considering structural effect[J].Rock and Soil Mechanics,2007,28(11):2284－2290.

[8]LIU M D,CARTER J P,DESAI C S.Modeling compression behavior of structured geomaterials[J].International Journal of Geomechanics,2003,3(2):191－204.

[9]刘恩龙,沈珠江.结构性土的强度准则[J].岩土工程学报,2006,28(10):1248－1252.LIU En-long,SHEN Zhu-jiang.Strength criterion for structured soils[J].Chinese Journal of Geotechnical Engineering,2006,28(10):1248－1252.

[10]邓国华,邵生俊,佘芳涛.结构性黄土的修正剑桥模型[J].岩土工程学报,2012,34(5):835－841.DENG Guo-hua,SHAO Sheng-jun,SHE Fang-tao.Modified cam-clay model of structured loess[J].Chinese Journal of Geotechnical Engineering,2012,34(5):835－841.

[11]殷杰.结构性软黏土的修正剑桥模型[J].工程力学,2013,30(1):190－197.YIN Jie.A modified Cam clay model for structured soft clays[J].Engineering Mechanics,2013,30(1):190－197.

[12]陈晓平,杨光华,杨雪强.土的本构关系[M].北京:中国水利水电出版社,2011.CHEN Xiao-ping,YANG Guang-hua,YANG Xue-qiang.Constitutive relation of soils[M].Beijing:China Water Power Press,2011

[13]刘祖典.黄土力学与工程[M].西安:陕西科学技术出版社,1997.LIU Zu-dian.Mechanics and engineering of loess[M].Xi'an:Shaanxi Science and Technology Press,1997.

[14]ZHONG Zu-liang,LIU Yuan-xue,LIU Xin-rong,et al.Influence of moisture content on shearing strength of unsaturated undisturbed quaternary system middle Pleistocene[J].Journal of Central South University,2015,22(7):2776－2782.

[15]张学言.岩土塑性力学[M].北京:人民交通出版社,1993.ZHANG Xue-yan.Geotechnical plastic mechanics[M].Beijing:China Communications Press,1993.