RV减速机针摆传动齿面接触特性分析

黄津晶，吴 锐，罗 涛

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070；2.现代汽车零部件技术湖北省重点实验室，湖北 武汉，430070)



RV减速机针摆传动齿面接触特性分析

黄津晶1,2，吴 锐1,2，罗 涛1,2

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070；2.现代汽车零部件技术湖北省重点实验室，湖北 武汉，430070)

基于RV减速机的传动和受力特点，在ANSYS中建立了摆线轮与针齿啮合的有限元模型，通过提取参与啮合的19个齿面上的节点数据，分析了啮合作用力、最大接触应力及接触区域的变化规律，并将摆线轮转动了6个角度，研究在不同啮合角度下摆线轮的受力情况及参与啮合的各齿面上接触力、接触应力和接触区域的变化趋势。

摆线轮；针轮；接触应力；啮合作用力；接触区域

RV减速机是在摆线针轮基础上发展起来的一种新型传动机构。它具有体积小、质量轻、传动比大、效率高等一系列优点，比传统的摆线针轮行星传动机构具有更小的体积、更大的刚性和过载能力，且抗冲击性能也提高很多[1]，因此目前被广泛应用于数控机械行业，尤其是工业机器人领域。

国内外诸多学者对RV减速机进行了较为广泛的研究，其研究重点主要集中在动力学性能[2-3]、传动精度及修形优化方面，包括RV减速机的动力学建模方法[4]、固有频率研究[5]、刚度计算[6-8]，以及虚拟样机仿真技术[9-11]；研究传动误差变化曲线[12-14]，分析计算RV减速机的回差[15-16]；提出了不同的修形优化方案[17-19]，以提高减速机的运动精度、传动效率，保证其回差小、刚度和承载能力大。在上述研究中，部分学者进行了有限元分析，但仅仅是简单提取齿面上的应力值来验证模型的正确性，作为研究修形、误差等的前提条件。也有学者重点研究了摆线轮针齿传动部分的齿面接触情况[20]，但却将摆线轮针齿模型简化为平面问题，忽略了齿向接触区域的变化，无法全面反映齿面的实际接触情况，且尚未研究单一齿面上及其啮合过程中齿面上的啮合作用力、接触应力、接触区域的分布和变化规律。针对上述不足，笔者以RV减速器中摆线轮针齿齿面接触状态为研究重点，较全面地研究了摆线轮与针齿在啮合过程中的接触特性。

1 RV传动的理论计算

1.1 摆线轮标准齿形方程

RV传动的核心部件为摆线轮，其齿廓有两种生成方法：①半径较小的滚圆在半径较大的基圆上作纯滚动，两圆外切，滚圆半径上某一点的运动轨迹即为摆线；②半径较大的滚圆套在半径较小的基圆外侧纯滚动，基圆内切于滚圆，滚圆半径上某一点的运动轨迹即为摆线。两种生成方法可以生成同一条摆线[21],如图1所示。

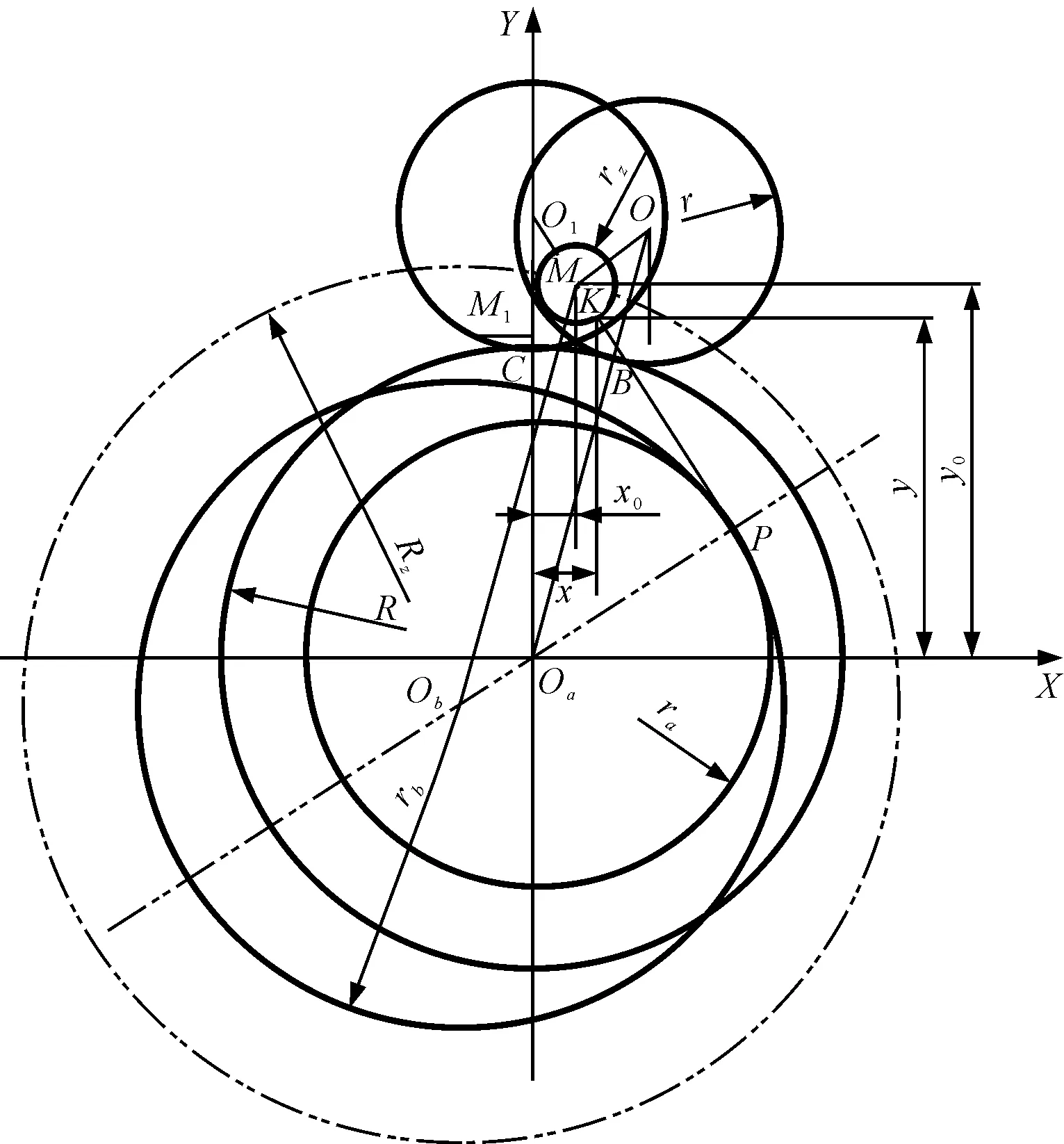
图1 摆线的两种生成方法

根据摆线的生成原理，可得出摆线轮标准齿形方程。以第一种生成方法为例，滚圆从基圆上C点滚动到B点的过程可分解为滚圆绕基圆圆心旋转了α，绕自身圆心旋转了φ，即相对转角，则绝对转角为β=α+φ。由于滚圆转过一周对应生成一个齿，那么φ=zcα，β=α+φ=α+zcα=zpα。M点的坐标为摆线轮理论齿廓的齿形方程，而实际齿廓应当是节点P与圆心M的连线与圆M圆周的交点K的坐标轨迹，其方程为：

(1)

式中:rrp为针齿半径;K1为短幅系数;zc、zp分别为摆线轮与针轮的齿数，φ为啮合相位角。

1.2 摆线轮与针齿的受力分析

图2为摆线轮的受力分析图，由图2可知摆线轮有一半齿参与了啮合，每个齿上的作用力均指向瞬心P。

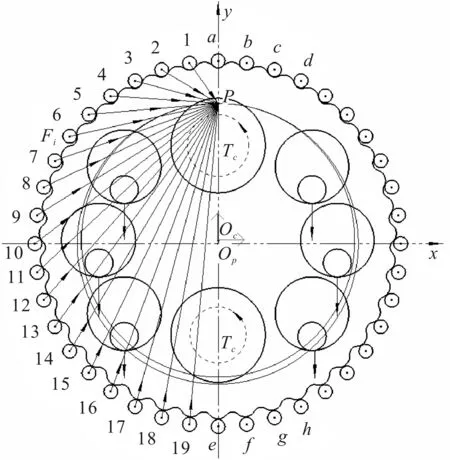
图2 摆线轮的受力分析

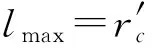
(2)

式中:Tc为输出轴传递给摆线轮的扭矩；ψi为针齿相对于针齿分布圆圆心的转角；rp为针齿分布圆半径。

1.3 摆线轮与针齿齿面接触计算

根据理论齿形方程可计算出理论齿廓的曲率半径ρ0，实际齿廓的曲率半径ρ=ρ0+rrp，即：

(3)

根据赫兹公式，齿面接触应力为：

(4)

其中摆线轮的材料采用轴承钢GCr15，取当量弹性模量Ec=2.06×105MPa。以表1中的参数设计摆线轮与针齿并进行计算。

表1 摆线轮与针齿设计参数

理论上摆线轮共有一半的齿(即19个齿)参与啮合，将这19个齿与针齿接触的齿面依次从1～19编号，如图2所示。将设计参数代入齿面载荷与齿面接触应力计算式，可得到19对针齿与摆线轮齿啮合的作用力及19个摆线轮齿面上的最大接触应力，其分布如图3所示。由图3可知，啮合作用力与接触应力曲线的分布规律均为先增大后减小，且同时在4号齿面上取到最大值。其中摆线轮齿面接触应力的最大值σHmax=587 MPa，小于轴承钢GCr15许用接触应力σHp=1 200 MPa。

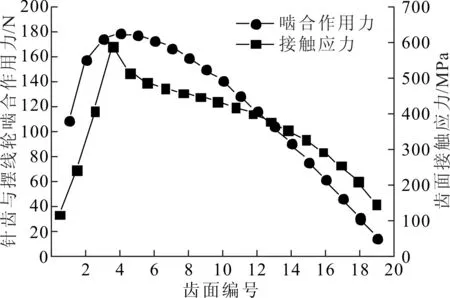
图3 齿面上的啮合作用力及最大接触应力

2 有限元建模与计算

2.1 有限元模型的建立

根据摆线轮的标准齿形方程在Matlab中生成一个齿廓上的181个数据点，并将其坐标导入ANSYS中生成关键点，样条拟合后生成摆线轮齿廓曲线，按照设计参数在ANSYS中建立摆线针轮的三维模型。

由于研究重点是摆线轮齿与针齿的齿面接触特性，为了简化计算，模型删除了摆线轮中心部分的结构以作简化，简化后的模型如图4所示。同时对摆线轮齿与针齿接触的部分进行了网格细化，如图5所示。

图4 摆线轮简化模型

图5 啮合对网格局部放大图

分别以摆线轮齿与针齿接触面上的节点为对象建立接触对，如图6所示。在针齿圈外圈节点上施加全约束，摆线轮中心孔内圈节点在柱坐标下约束其绕x、z轴的旋转。两个摆线轮传递的转矩Tc=126.5 N·m，加载时，在摆线轮中心孔节点上施加切向的作用力，由于中心孔上的节点均匀分布，故每个节点分到相等的力，其大小为FY=Tc/(2RN)，其中R为中心孔半径，N为中心孔上节点数。边界条件及载荷施加情况如图7所示。

图6 接触对局部放大图

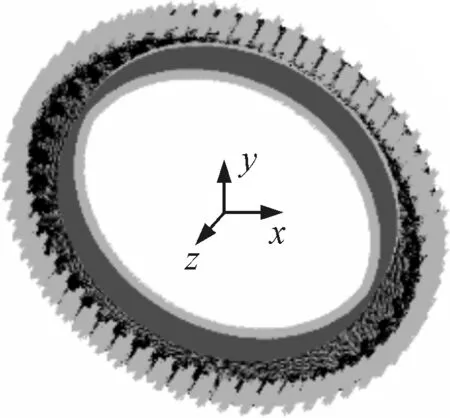
图7 边界条件及载荷施加

2.2 齿面接触应力及接触区域分布情况

获得摆线轮轮齿表面的接触应力分布及接触区域如图8所示。该接触状态下，共有 19对齿参与啮合，接触区域呈带状。

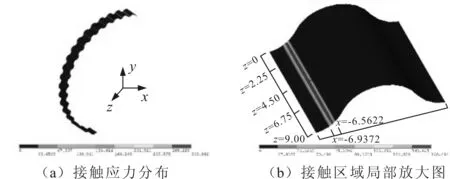
图8 摆线轮齿面接触应力分布及接触区域

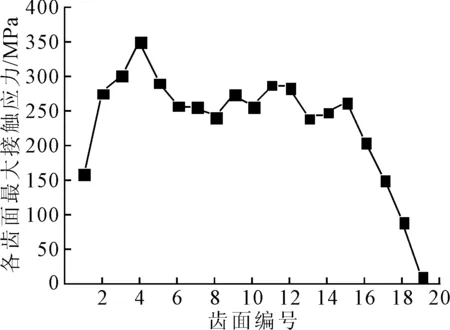
图9 有限元计算的各齿面上最大接触应力

分别提取19个齿面上的最大接触应力，如图9所示，有限元计算结果在8～16号齿之间存在小幅波动，曲线整体符合先增后减的规律，且在第4个齿上取得最大值，为351.83 MPa，与赫兹公式计算结果的变化规律趋于一致。

摆线轮齿面上节点坐标的分布方向如图8(b)所示，z轴平行于齿宽方向，x轴垂直于齿宽方向。划分网格时，在z轴方向以0.45 mm为间距划了20等分。以1号齿面为研究对象，分别在z=0，z=0.45，z=2.25，z=4.50，z=6.75，z=8.55，z=9.00处作截面垂直于z轴，提取各个截面上节点的接触力，如图10所示。可见在截面与齿面接触区域的交线上，节点的接触力由两侧向中间递增，在中间位置达到最大值。比较7个截面上的数据可见在两端面处，节点接触力整体有明显下降，z=0，z=9.00两条接触力曲线处于其余5条曲线的下方。

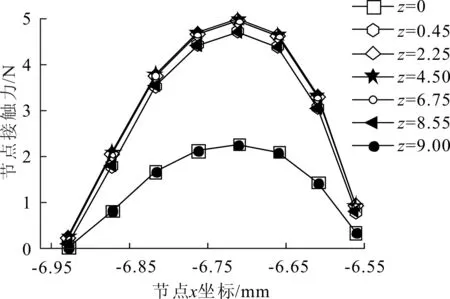
图10 截面上节点接触力分布

仍取1号齿面为研究对象，该齿面上的接触区域在x轴上的分布如图8(b)所示。在x=-6.937 2，x=-6.879 8，x=-6.823 5，x=-6.728 5，x=-6.714 9，x=-6.662 5，x=-6.611 6，x=-6.562 2处作截面垂直于x轴，提取各个截面上节点的接触力，如图11所示。在z=0，z=9.00处的节点接触力较小，处于中间区域的节点接触力较大且稳定在同一值。随着节点横坐标x的增大，节点接触力曲线先上移，后下降，最大值在中间位置(x=-6.714 9)处取到。

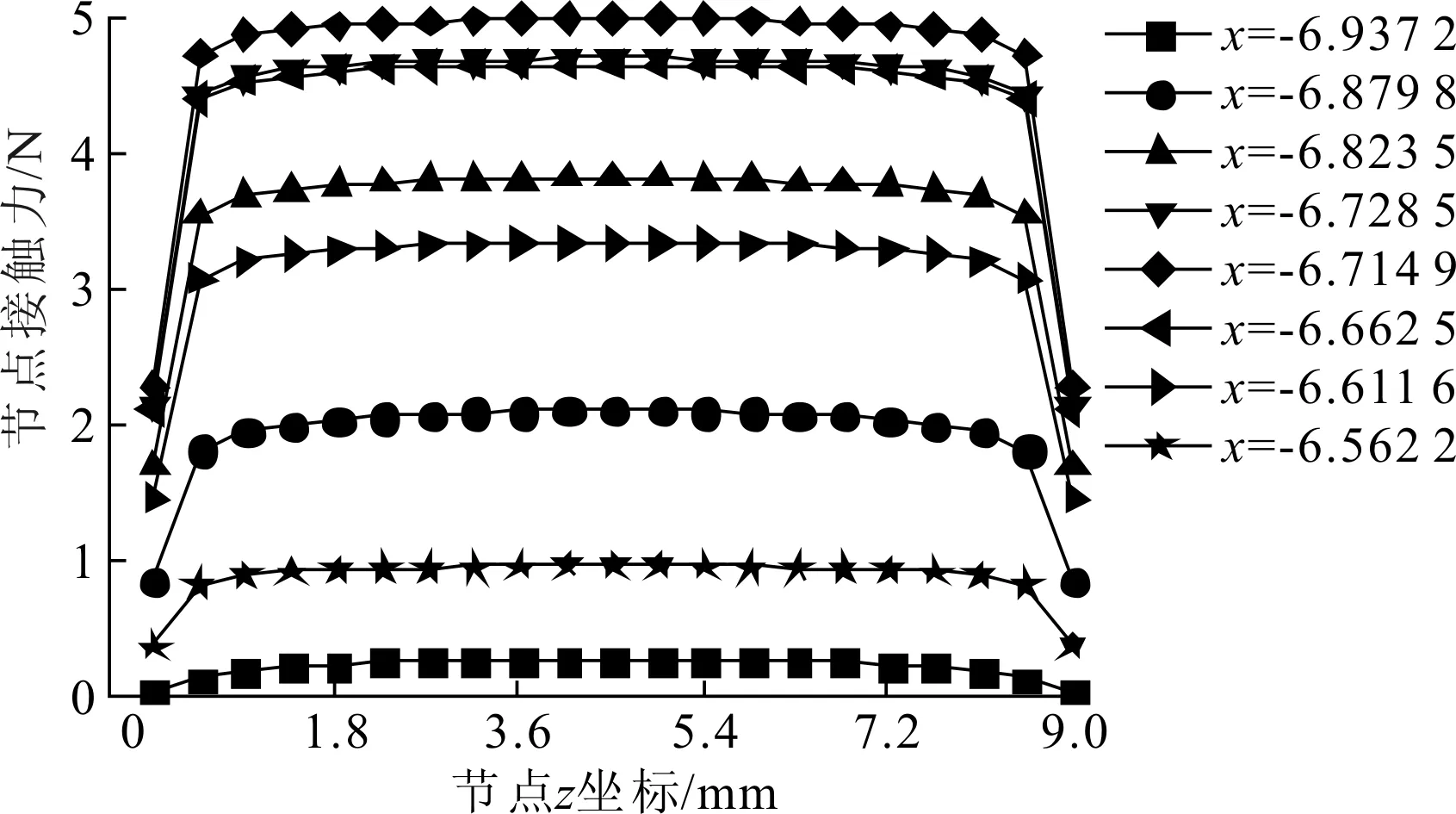
图11 截面上节点接触力分布

综合分析图10和图11，可知接触区域并非严格呈单一带状，而是条纹外侧接触应力小，中心接触应力大，两端面处接触应力小，中间区域接触应力大，接触区域近似鼓形。

2.3 啮合过程齿面接触应力及接触区域变化

笔者讨论了单一啮合状态下摆线轮上参与啮合的19个齿面上的最大接触应力分布规律、某一个齿面上啮合作用力的变化趋势及接触应力的分布情况，为了研究在啮合周期内摆线轮齿面上啮合作用力和接触应力的变化情况，将摆线轮转动了6个角度，获得摆线轮齿与针齿从啮入到啮出过程中的6个啮合状态。由于摆线轮是绕自身圆心的自转与绕针齿分布圆圆心的公转同时进行的复合运动，故在旋转摆线轮时也将其角度分解为自转角度和公转角度，如表2所示，其中角度值取顺时针为正，逆时针为负。

表2 摆线轮旋转角度

对旋转后的6种啮合状态进行有限元计算。规定图4中摆线轮与针齿的啮合状态对应旋转角为θ0，则θ1相对于θ0有a、b、c、d(见图2)4个齿进入啮合，16～19号齿退出啮合；θ2状态下a～c齿进入啮合，17～19号齿退出啮合；θ3状态下a、b齿进入啮合，18、19号齿退出啮合；θ4状态下e、f齿进入啮合，1、2号齿退出啮合；θ5状态下e～g齿进入啮合，1～3号齿退出啮合；θ6状态下e～h齿进入啮合，1～4号齿退出啮合。每个状态下均有19对齿参与啮合，对应的19个摆线轮齿面上的最大接触应力分布情况如图12所示。

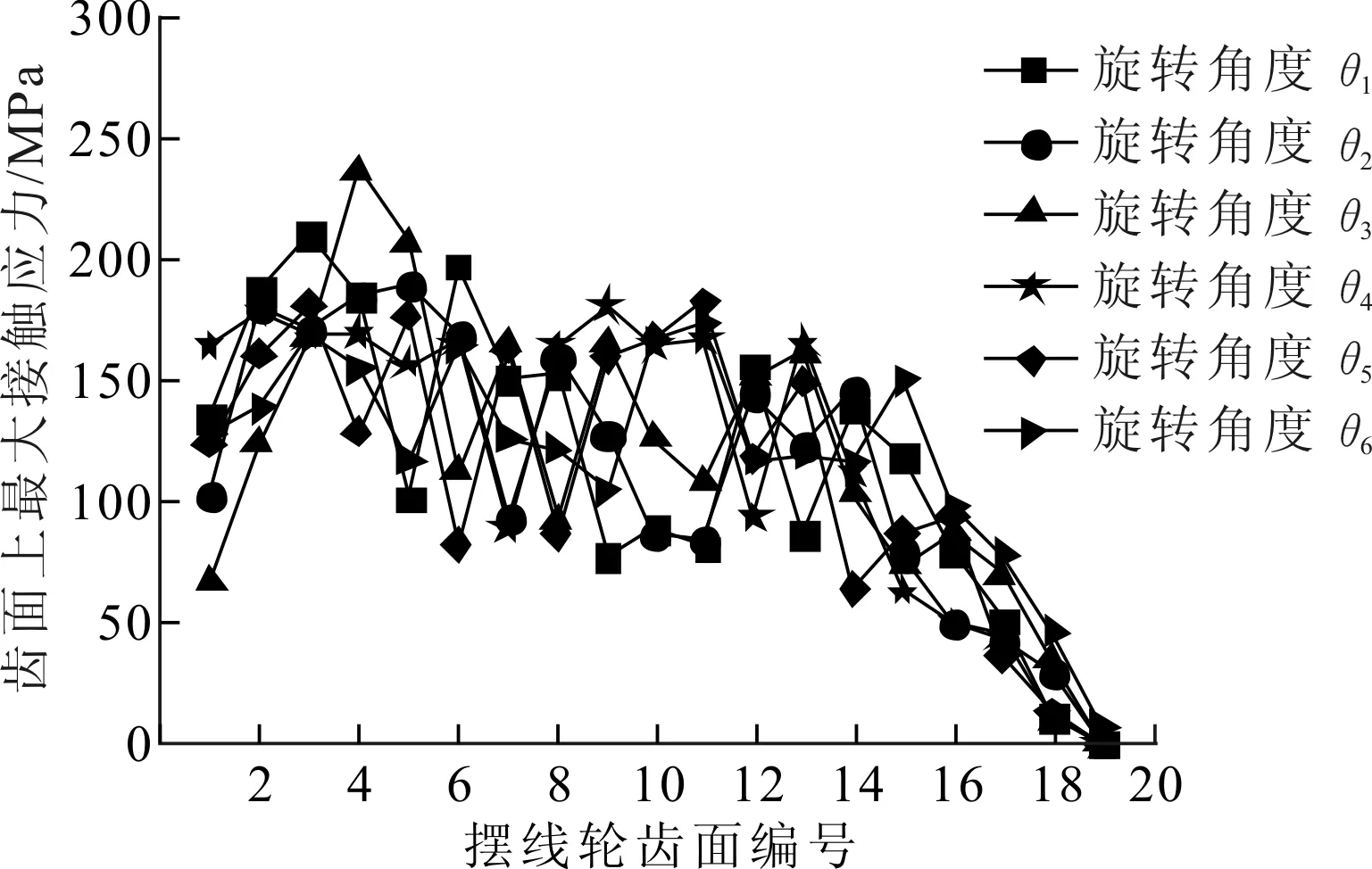
图12 不同旋转角下摆线轮齿面上最大接触应力

6个旋转角下对应的19个齿齿面上的最大接触应力在数值上存在波动，但观察6条曲线的分布规律，可发现其变化趋势是一致的，均为先增大后减小，且在4号齿附近取到最大值。

以θ0状态下摆线轮上3、4、5号齿齿面为研究对象，观察在旋转过程中这3个齿面上最大接触应力的变化，如图13所示。

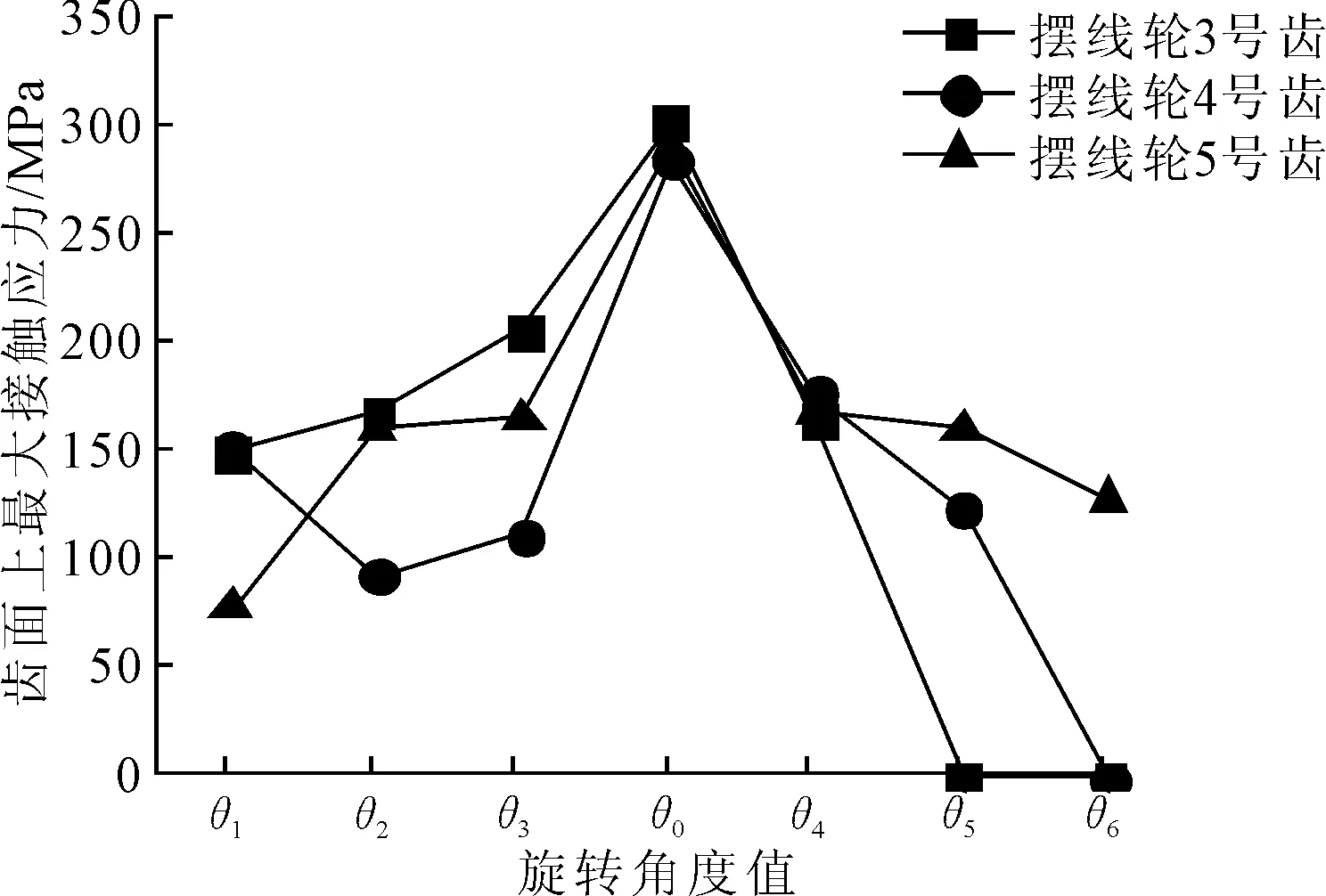
图13 不同旋转角下3、4、5号齿齿面上最大接触应力变化

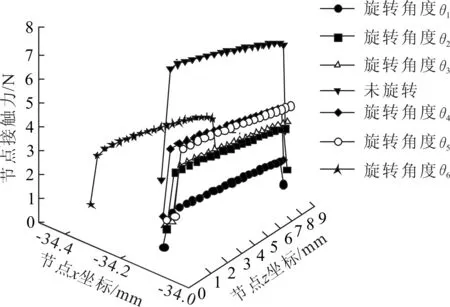
图14 不同旋转角下齿面上最大接触力分布

3个齿上的最大接触应力均在θ0状态下取到峰值。3号齿在旋转角为θ5时退出啮合，4号齿在旋转角为θ6时退出啮合，而5号齿始终参与啮合。以5号齿齿面为对象研究齿面上最大节点接触力及接触区域分布的变化。对于每个旋转角度下齿面上的数据，将x、y坐标相同的21个节点划分为一组，选择节点接触力最大的一组数据作为该角度下的比较样本，共获得7条曲线，如图14所示。7条曲线均在z=0，z=9处的节点上取到最小值，在中间区域维持稳定值。在旋转角度从θ1到θ0再到θ6的变化过程中，节点接触力曲线先上升后下降，在θ0处取到最大值。同时，节点的x坐标减小，这说明5号齿齿面上的接触区域发生了从齿根方向向齿顶方向的偏移。

3 结论

在ANSYS中建立了摆线轮与针齿啮合的三维模型，分析了参与啮合的19个摆线轮齿面上的啮合作用力、最大接触应力和接触区域分布后，取摆线轮与针齿在传动过程中的6个啮合角度，得到了每个啮合角度下摆线轮齿面上啮合作用力、最大接触应力和接触区域的变化规律：

(1)理论分析与有限元计算结果对应的摆线轮齿面上啮合作用力及接触应力曲线具有一致的变化趋势，且均在第4个齿上达到峰值。

(2)按平行齿宽方向和垂直齿宽方向所提取齿面的数据曲线反映了摆线轮与针齿的啮合区域近似鼓形，即条纹外侧接触应力小，内侧接触应力大，两端面处接触应力小，中间区域接触应力大。

(3)将摆线轮转动6个角度，每个旋转角度下对应啮合的19个摆线轮齿面上的最大接触应力的变化趋势一致，均在第4个齿附近取到峰值。不同旋转角下参与啮合的齿始终保持在19对，啮入齿数与啮出齿数相等。对于某一齿从啮入到啮出的过程中，其齿面上的最大接触应力先增大后减小，其接触区域也在传动过程中发生了从齿根方向向齿顶方向的偏移。

[1] 齿轮手册编委会.齿轮手册 [M].北京:机械工业出版社，2010：40-45.

[2] 张丰收，张琳琳，刘建亭，等.RV减速器动态特性研究综述[J].机械传动，2014(8)：174-176.

[3] CHIU-FUN H.Dynamics analysis of cycloidal speed reducers with pinwheel and nonpinwheel designs[J]. Journal of Mechanical Design，2014(136)：107-111.

[4] 赵慧，张红梅.基于SolidWorks软件的2K-V型减速机数字化建模及运动仿真[J].装备制造技术，2015(1)：28-30.

[5] 杨玉虎，朱临宇，陈振宇，等. RV减速器扭转刚度特性分析[J].天津大学学报，2015，48(2)：111-118.

[6] 聂松辉，颜彧.RV减速器输出机构扭转刚度分析[J].机械设计与研究，2014，30(4)：24-26.

[7] 张迎辉，肖君君，何卫东.机器人用RV减速器针摆传动啮合刚度计算[J].大连交通大学学报，2010，31(2)：20-23.

[8] 何卫东，陆岩，吴鑫辉.基于等价模型的RV减速器扭转刚度计算[J].机械传动，2013(9)：38-41.

[9] LUCIA P,PAUL C P,LUMINITA D,et al.Modeling and simulation of cycloid curves with application in robotics[J].Revista Fiabilitate si Durabilitate，2010，2(6)：23-28.

[10] 姜振波.RV减速器虚拟样机仿真技术研究[J].机械传动，2014(9)：20-23.

[11] 陈来利，姚辰龙，王海生.基于ADAMS的RV减速器虚拟样机设计与仿真分析[J].制造业信息化，2013(9)：102-105.

[12] 杨玉虎，张洁，许立新.RV传动机构精度分析[J].天津大学学报(自然科学与工程技术版)，2013，46(7)：623-628.

[13] BLANCHE J G ，YANG D C H.Cycloid drives with machining tolerances[J].Journal of Mechanisms Transmissions and Automation in Design，1989(111)：337-344.

[14] QI H J, ZHANG D W, LIU Z X. A dynamic measuring system for transmission error of high precision 2K-V type speed reducer with cycloid gear[J]. The International Conference on Mechanical Transmissions，2006(6)：283-287.

[15] 邓效忠，张艳珍，李天兴，等.RV减速器摆线针轮传动精度控制的研究现状及需要解决的技术问题[J].机械传动，2015(2)：162-165.

[16] 李充宁，蔡胜，杨保占. 2K-V型摆线针轮减速机回差与刚度的试验研究[J].机械设计，2014，31(1)：33-37.

[17] 刘洪建，李刚，胡小平.RV减速器摆线轮的修形[J].机械工程师，2014(1)：82-83.

[18] 赵铮. RV320工业机器人减速器中摆线齿廓的修形[J].机电设备，2014(4)：33-35.

[19] 关天民，张东生，雷蕾.FA新型摆线轮行星传动受力分析方法与齿面接触状态有限元分析[J].机械设计，2005，22(3)：31-34.

[20] MANFRED C,ANTONI J.FEM in numerical analysis of stress and displacement distributions in planetary wheel of cycloidal gear[C]∥Numerical Analysis and It’s Applications Second International Conference.[S.l.]:[s.n.],2000：772-779.

[21] 郑州工学院机械原理及机械零件教研室.摆线针轮行星传动[M].北京：科学出版社，1978：12-43.

HUANG Jinjing:Postgraduate; School of Automotive Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

Tooth Contact Analysis of Cycloid Drive in RV Reducers

HUANGJinjing,WURui,LUOTao

On the basis of the transmission and loading features of RV reducers, a 3D model of cycloid gear meshing with pins was established in ANSYS to do the finite element method calculation. By fetching the node data on the engaged 19 tooth surfaces, the varying pattern of contact force, contact stress and contact area were studied. By the meanwhile, to focus on the change of force condition and contact situation under various postures, the cycloid gear was rotated to different statuses.

cycloid gear; pins; contact stress; meshing force; contact area

2015-05-09.

黄津晶(1990-)，女，浙江诸暨人，武汉理工大学汽车工程学院硕士研究生.

湖北省重大科技成果转化与产业化基金资助项目(2012AAA07-01).

2095-3852(2015)06-0720-06

A

TH132.414；TH123

10.3963/j.issn.2095-3852.2015.06.013