焊接翻边对薄壁梁吸能特性的影响研究

王 峰，莫易敏，吕俊成,，黄 峰，林智桂

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2. 上汽通用五菱汽车股份有限公司，广西 柳州 545007)



焊接翻边对薄壁梁吸能特性的影响研究

王 峰1，莫易敏1，吕俊成1,2，黄 峰1，林智桂2

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2. 上汽通用五菱汽车股份有限公司，广西 柳州 545007)

基于数值模拟，研究了焊接边宽度及新型焊接边设计对双帽形薄壁梁吸能特性的影响。动态落锤试验结果证明，宽度的增加和新型焊接边设计均可有效提高平均压溃力与比吸能。

双帽形薄壁梁；焊接翻边；轴向冲击；能量吸收

作为能量吸收结构主要形式的薄壁梁被广泛用于改善车辆耐撞性[1]。在矩形、正六边形、槽型等不同截面形状薄壁梁简化模型的众多研究中，重点对不同截面形状薄壁梁的优缺点进行比较[2-3]。但是由于汽车设计的约束，非矩形截面薄壁梁在汽车吸能结构的应用发展较为受限。帽形薄壁梁由于其结构规整、方便，在汽车安全碰撞结构设计中被广泛采用。笔者对双帽形薄壁梁进行研究，通过仿真与试验分析焊接翻边的宽度与设计对薄壁梁吸能特性的影响。

1 双帽形薄壁梁的吸能特性

图1所示为双帽形薄壁梁的截面形式，a为长边长度，b为宽边长度，f为翻边长度。笔者取双帽形薄壁梁为等边长，即C=a=b,采用非线性有限元软件HYPERMESH/LS-DYNA进行仿真研究，单元网格大小为2.5 mm。图2所示为薄壁梁轴向冲击仿真模型及落锤试验工装图。

图1 双帽形薄壁梁的截面形式

图2 薄壁梁轴向冲击仿真模型及落锤试验工装图

在轴向冲击工况下，双帽形薄壁梁的动态力学行为类似于正方形和矩形截面箱形管。对于双帽形薄壁梁，在发生轴对称折叠压溃时[4-6]，有：

Pm/m0=52.20(l/t)1/2

(1)

式中:Pm为接触面上的平均撞击力；m0=σ0t2/4为横截面的塑性失效弯矩(每单位周长)；l为截面长，l=2a+2b+4f=4(C+f);t为壁厚。

笔者应用Cowper-Symonds本构关系，计入屈服应力随应变率增大而增大的影响，对屈服应力进行修正：

(2)

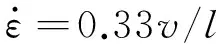
(3)

52.20(l/t)1/2×[1+(0.33v/lB)1/q]

(4)

薄壁梁吸收碰撞能量的另外一个指标为比吸能SEA值[8-10]，其计算公式为：

SEA=PmH/m

(5)

双帽形薄壁梁发生轴向压溃时，其塑性破损模式可能是轴对称的或者是非轴对称的，也可能出现弯曲变形，而变形形式取决于长宽比、厚度、高度，以及焊接边等结构参数。笔者对双帽形薄壁梁的变形形式进行定义，以便后续数据统计的需要。薄壁梁轴向压溃变形模式如图3所示，图3(a)为薄壁梁渐进式轴向压溃(P压溃模式)，其特点为梁壁经历了严重的向内和向外的塑性变形，褶皱紧凑并连续且呈现轴对称模式，焊接边与褶皱变形同步、规律性明显；图3(b)为薄壁梁方管式轴向压溃，即非紧凑型破损模式(S压溃模式)，其特点是薄壁梁轴向压溃不规律，褶皱形成不稳定并呈现非对称、不连续的模式，焊接边变形与褶皱形成并无规律，该模式整体上相对不稳定，有发生Euler屈曲的趋势，是薄壁梁设计不希望出现的能量耗散结构；图3(c)为薄壁梁不规则轴向压溃(I压溃模式)，其特点是薄壁梁轴向压溃不规则，发生褶皱变形，同时也会发生其他结构变形(塌陷、内弯等)，但并未出现薄壁梁明显弯曲；图3(d)为薄壁梁弯曲变形(B压溃模式)，其主要表现为在发生轴向压溃的同时薄壁梁弯曲变形明显，薄壁梁下端发生弯曲失稳。

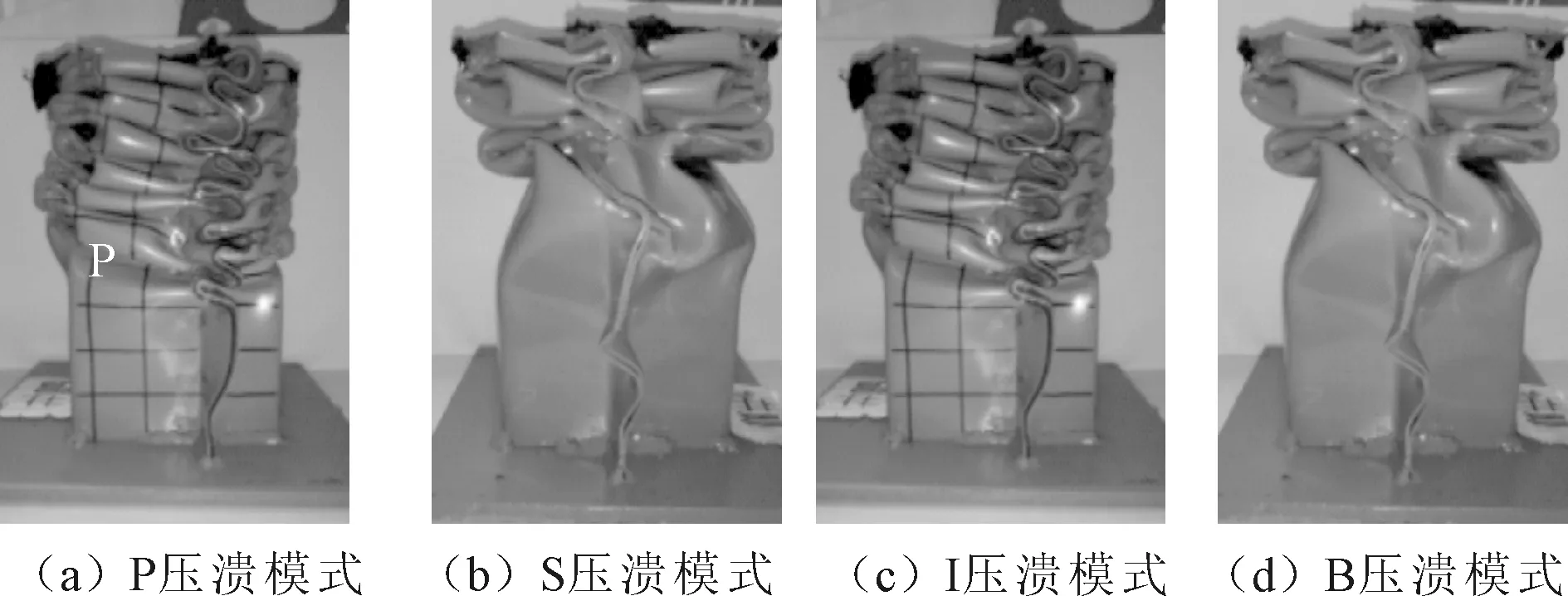
图3 薄壁梁轴向压溃变形模式

2 焊接翻边的吸能影响仿真分析

2.1 焊接翻边宽度的影响

笔者基于数值模拟的方法研究双帽形薄壁梁焊接翻边对吸能特性的影响。薄壁梁有限元模型为等截面，即a=b=85mm，f∈(15,30)mm。设计16组样本模型分析焊接翻边宽度对轴向冲击下的薄壁梁吸能影响。图4为平均压溃力随焊接翻边变化的趋势图。等截面双帽形薄壁梁，平均压溃力随焊接翻边f的增加而升高；SEA随焊接翻边的增加而升高。对比f=30mm与f=15mm的模型，SEA提高约20%。同时，由样件变形模式分析得到，较大的翻边长度有助于薄壁梁形成稳定的变形，不易发生弯曲、内陷等不合理变形；相反，较小的翻边长度不仅会大幅降低SEA值，更容易出现弯曲等不良变形。

图4 平均压溃力随翻边宽度变化趋势

2.2 对称斜向焊接翻边的吸能影响

基于传统的双帽形薄壁梁结构形式，笔者提出对称斜向焊接边的双帽形薄壁梁的新型结构，如图5所示。θ为斜向焊接边与薄壁梁中轴线的夹角，从前后视图可观察到两焊接边对称交叉。

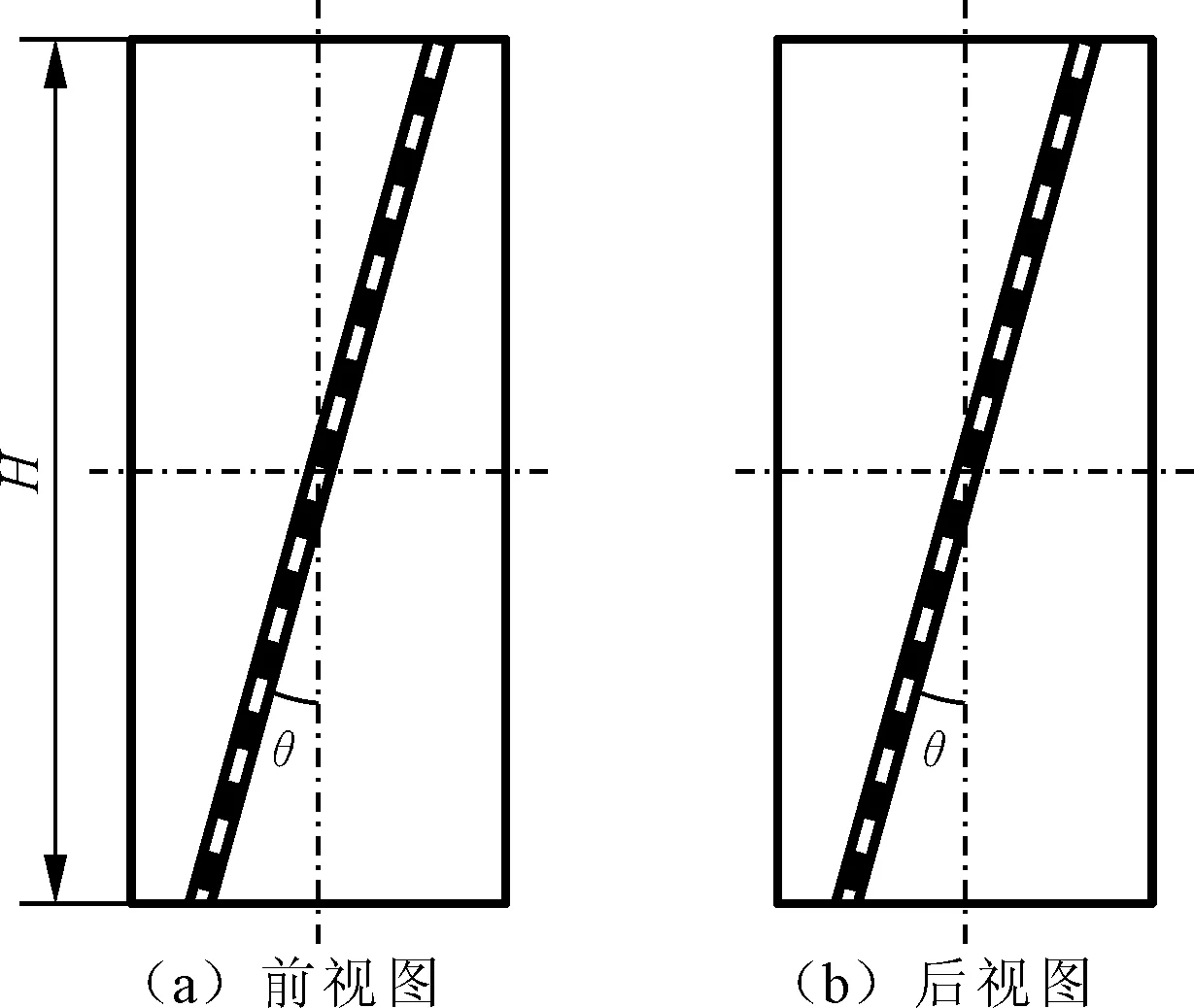
图5 对称斜向焊接边双帽形薄壁梁

对称斜向焊接边对轴向冲击下的双帽形薄壁梁的仿真试验，根据倾斜角、长高比、厚度与边长比、焊接边宽度与边长比等无量纲参数进行试验，验证斜向焊接边薄壁梁具有良好的吸能特性，即可改进变形模式不好的传统双帽形薄壁梁轴向压溃，提升其轴向压溃的稳定性;同时，研究相关参数对薄壁梁变形模式、压溃力等的影响。

(1)倾斜角θ对变形模式的影响分析。薄壁梁在轴向载荷下，发生类似图3所示的变形。当薄壁梁发生图3(a)所示规则的“手风琴”式褶皱变形时，能够起到较好的变形吸能作用，其压溃力变化平稳有序；当发生其他3种变形时，可能导致整个部件进入欧拉弯曲等变形模式，失去原有设计的能量吸收能力。

通过仿真试验结果的统计，双帽形对称斜向焊接边薄壁梁参数θ的变化对薄壁梁的变形模式有至关重要的作用。笔者设计的薄壁梁模型高度均为H=400mm，f=20mm，t=1.4mm，边长设计范围为[45,95]且以10mm均布取值，考虑对称性设计要求及有限元模型建立需要，θ可选范围为[0°,9°]。表1为双帽形斜向焊接边薄壁梁仿真试验部分模型参数θ，各边长对应θ受可选范围影响逐渐减少，试验组数也相应降低。

表1 C=75 mm薄壁梁仿真试验模型统计表

在相同焊接边宽度f=20 mm，高度H=400 mm，t=1.4 mm的情况下，设计42组双帽形对称斜向焊接边薄壁梁模型仿真试验，分析薄壁梁倾斜角θ变化对变形模式的影响，如图6所示。通过42组仿真试验模型分析可以得到：

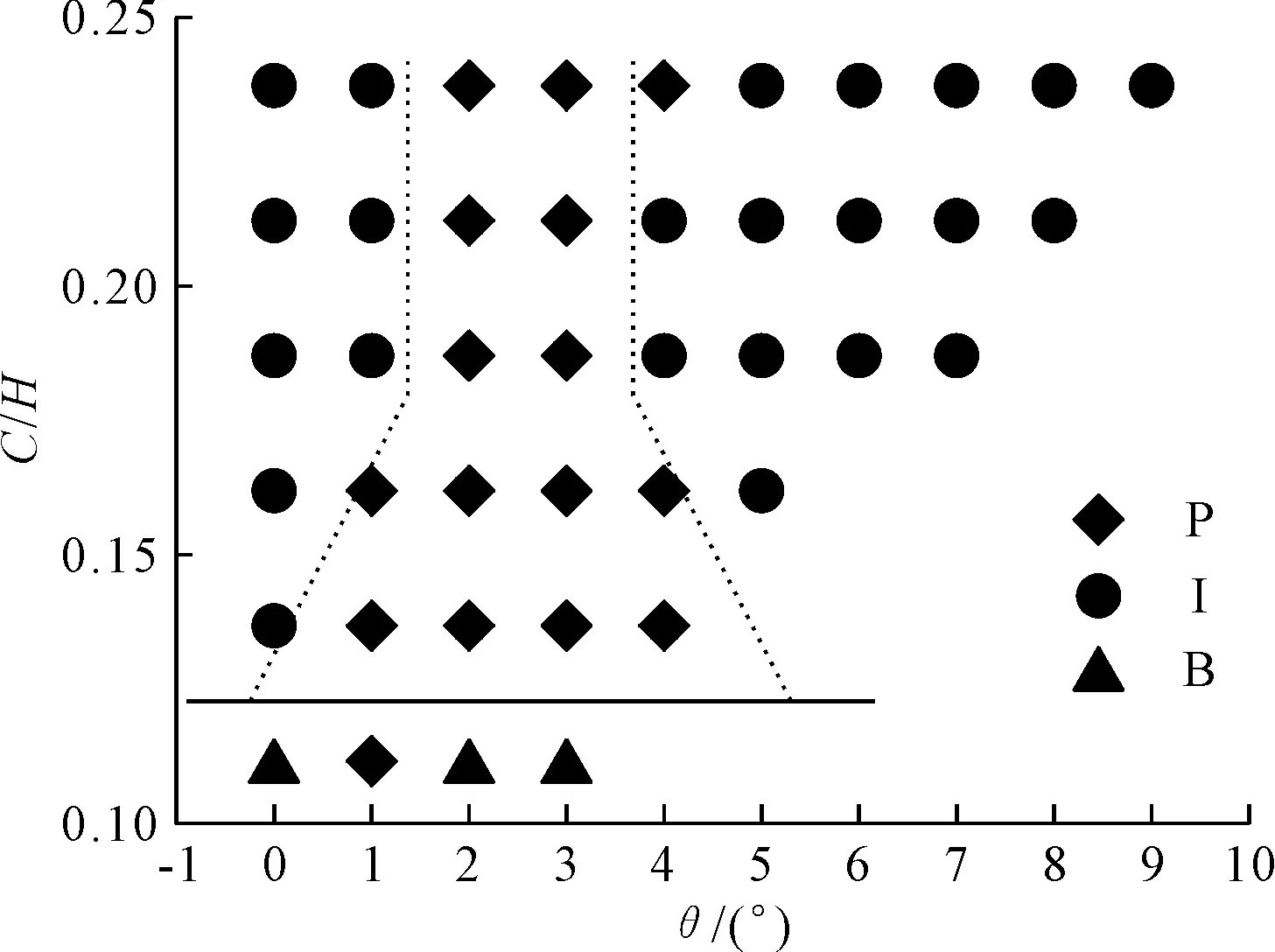
图6 θ和C/H影响薄壁梁变形模式的分析图

边长一定、倾斜角度不同的情况下，薄壁梁变形形式具有区间性。C/H∈(0.13,0.17)，倾斜角θ∈[1°,4°]的模型具有较好的渐进式变形，即P变形模式；C/H∈(0.17,0.25)，较好的渐进式变形P模式所对应的倾斜角θ区间收缩到[2°,3°]；同一边长下，不规则变形I模式对应的θ∈[5°,9°]具有共性，C/H∈(0,0.13)薄壁梁的变形模式以弯曲变形B模式为主。

倾斜角θ一定、边长不同的情况下，随着C/H的增大，变形模式受倾斜角θ区间的影响呈现3种趋势。θ∈{0°,5°,6°,7°,8°,9°}，薄壁梁模型的变形模式均为不规则变形；θ∈{2°,3°}，边长大于55 mm的薄壁梁模型具有良好的渐进式变形即P模式，一致性良好；θ∈{1°,4°}，随着C/H升高，变形模式由P模式向I模式转变，边长为95 mm、倾斜角度为4°的薄壁梁轴向压溃为渐进式变形即P模式。

双帽形对称斜向薄壁梁的变形模式呈现P、I、B这3种模式，弯曲变形B模式出现在C=45 mm的情况下，说明C/H低于0.13变形模式控制较为困难。薄壁梁的不规则变形I模式的出现，表明倾斜角度θ对模型变形有着重要影响，且较大的角度会使得变形不规则、脱离设计要求。与传统双帽形薄壁梁相比，对称斜向焊接边在不改变截面尺寸的情况下，通过改变焊接边斜向角度可使得θ=0°的传统双帽形薄壁梁的不规则变形模式(I模式)转化为渐进式变形模式(P模式)。同时，通过仿真试验数据统计，可得到倾斜角度θ的适应范围具有区间性且与多参数有关。

不同倾斜角度下，双帽形对称斜向焊接边薄壁梁的变形模式会出现渐进式、不规则式、弯曲式3种。图7为对称斜边薄壁梁变形模式，依次为倾斜角度0°、1°、2°、3°、4°、5°、6°、7°对称斜向焊接边薄壁梁模型0 ms、15 ms、30 ms时的轴向压溃变形。15 ms时，1°、2°、3°模型呈现较为稳定的渐进式压溃，褶皱有序形成，具有“手风琴”式的特征。同时，其他模型的变形已出现局部失稳现象及不规则压溃变形，0°、7°薄壁梁模型下端出现非弹性失稳现象可能导致其进入欧拉弯曲变形模式，4°、5°、6°薄壁梁模型在形成褶皱的过程中出现非渐进式的压缩变形且下端已出现失稳变形。30 ms时，通过观察模型褶皱情况可判断，2°、3°薄壁梁模型轴向压溃良好，褶皱形成具有典型的“手风琴”式特征。倾斜角为4°的薄壁梁模型在15 ms至30 ms变形过程中，出现了不规则失稳，导致其变形模式由P模式演变为I模式。其余模型因为在15 ms时即已出现非规则失稳破坏，因此其30 ms时的模型轴向压溃无论是皱褶还是其他变形结构都呈现变形过程中的不稳定和不规则性。

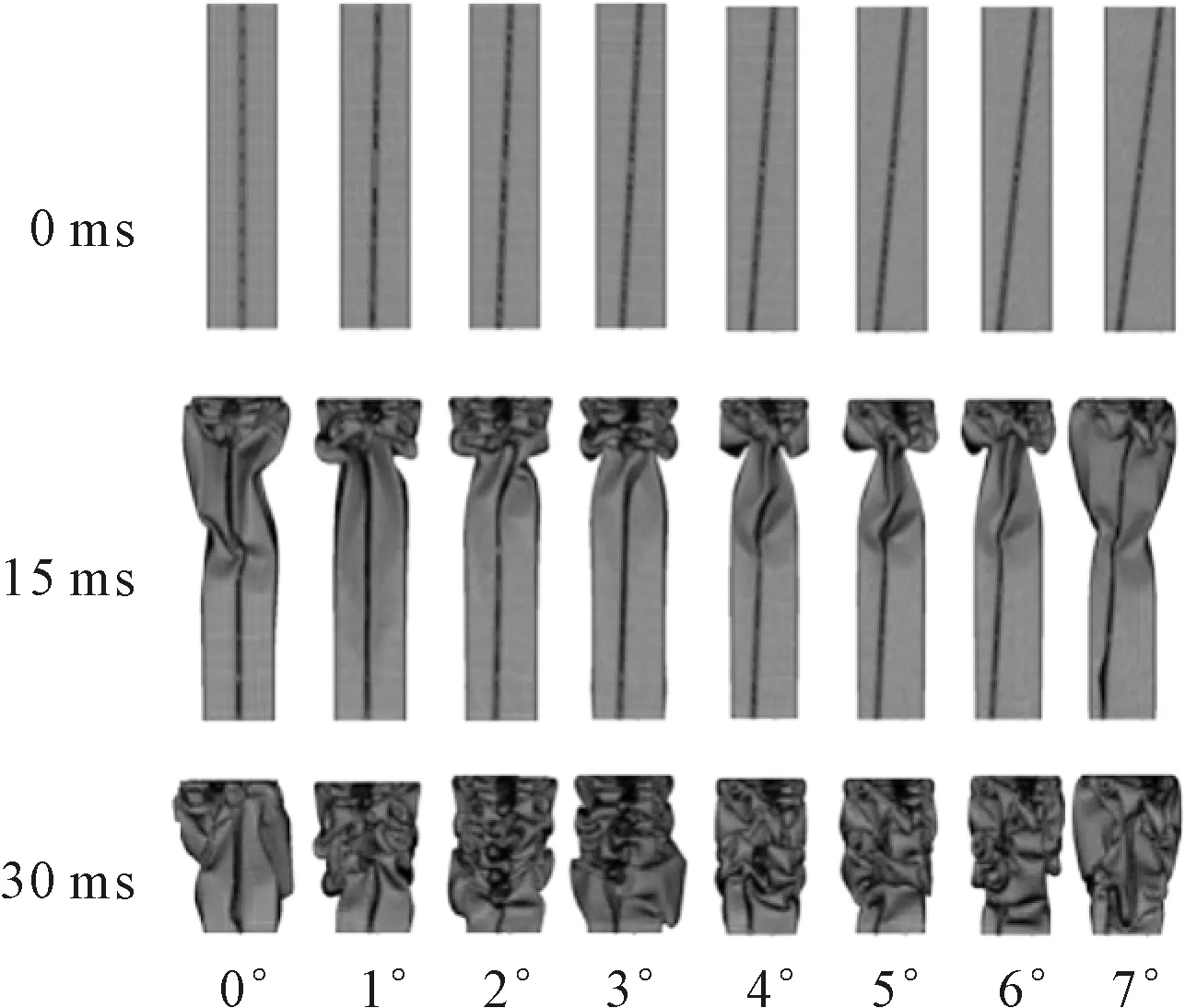
图7 C=75 mm对称斜边薄壁梁变形模式

(2)倾斜角θ对薄壁梁压溃力的影响分析。由于平均载荷对于诸如汽车碰撞加速度设计和预测等的重要性，大多数的研究都更为集中地关注薄壁梁轴向压缩的平均载荷。薄壁梁设计的不合理会造成压溃形式的不规则，继而使得平均轴向压溃力及能量吸收偏低。双帽形对称斜向焊接边薄壁梁的设计，通过改善变形模式以达到能量吸收要求，并保证平均压溃力可以满足设计要求。

图8为C=85 mm时的0°、2°、3°薄壁梁模型的位移-轴向压溃力图。由图8可知，倾斜角度为2°、3°的薄壁梁变形模式为渐进式，褶皱形成良好，且两薄壁梁模型的压溃力曲线特征相同、变化平稳，后续曲线最大载荷改变不大，最大载荷相对位移基本相同也可证明薄壁梁变形是渐进式变形。倾斜角度为0°的薄壁梁是传统薄壁梁的设计模型，因为出现类似内弯等非规则变形，造成压溃力曲线最大载荷明显高于倾斜角度为2°、3°的薄壁梁模型，其最大载荷相对位移偏大，可证明其变形形式为非渐进式的。因此，焊接边的对称斜向设计可改善薄壁梁压溃力趋势及其平稳性。同时，3°模型压溃形式的改善使其平均压溃力得到提高。仿真模型统计数据表明，其提升幅度可达到10%左右。

图8 0°、2°、3°模型的位移-轴向压溃力图

3 焊接翻边对吸能影响的试验验证

笔者通过仿真模型分析得出焊接边对双帽形薄壁梁吸能特性的影响规律，并通过图2(b)所示动态落锤试验设备进行验证。设备落锤最大质量可以达到2 000 kg，初始接触速度可达到15 m/s。笔者设定落锤质量为198 kg,初始速度为13.8 m/s。f=30 mm薄壁梁样件与仿真模型的动态冲击位移-压溃力曲线及变形如图9所示。样件试验与仿真模型的压溃力曲线较为吻合，平均压溃力误差小于5%，同时，两者的变形结果也基本一致。分析f=15、20、25 mm的样件试验结果均满足误差要求，从而可以证明，所建立仿真模型较准确，结果可信。

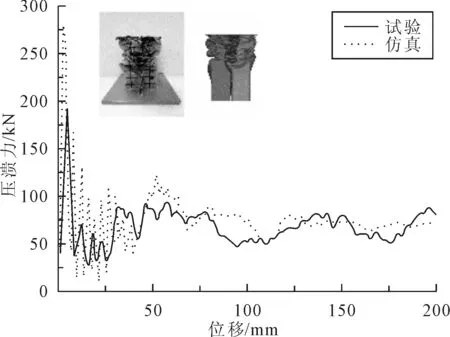
图9 f=30mm仿真模型与试验对比

焊接翻边宽度的变化对吸能特性的影响试验结果如表2所示。随着焊接翻边宽度的增加，平均压溃力与SEA值都有明显的增加，30 mm样件相较于15 mm有约20%的提高，与仿真模型的结果分析一致。4组样件动态冲击变形对比如图10所示，随着焊接翻边的增加，薄壁梁样件变形模式逐渐趋于稳定，减少或避免了不规则变形及弯曲内弯变形等现象。

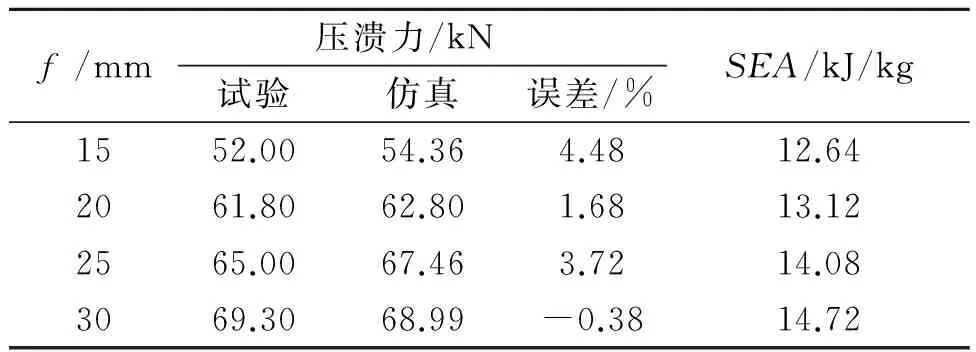
表2 焊接边宽度变化样件冲击试验结果

图10 焊接边宽度变化样件冲击变形

对称斜向焊接边设计薄壁梁的动态冲击验证选取关键样本点进行试验，即θ=0°和3°两个样件。图11和图12分别为0°和3°样件轴向冲击位移-压溃力曲线与变形对比图。相较于传统设计双帽形薄壁梁，θ=3°样件平均压溃力提升了16.8%，压溃形式紧凑且稳定，有效改善了传统设计薄壁梁的吸能特性。

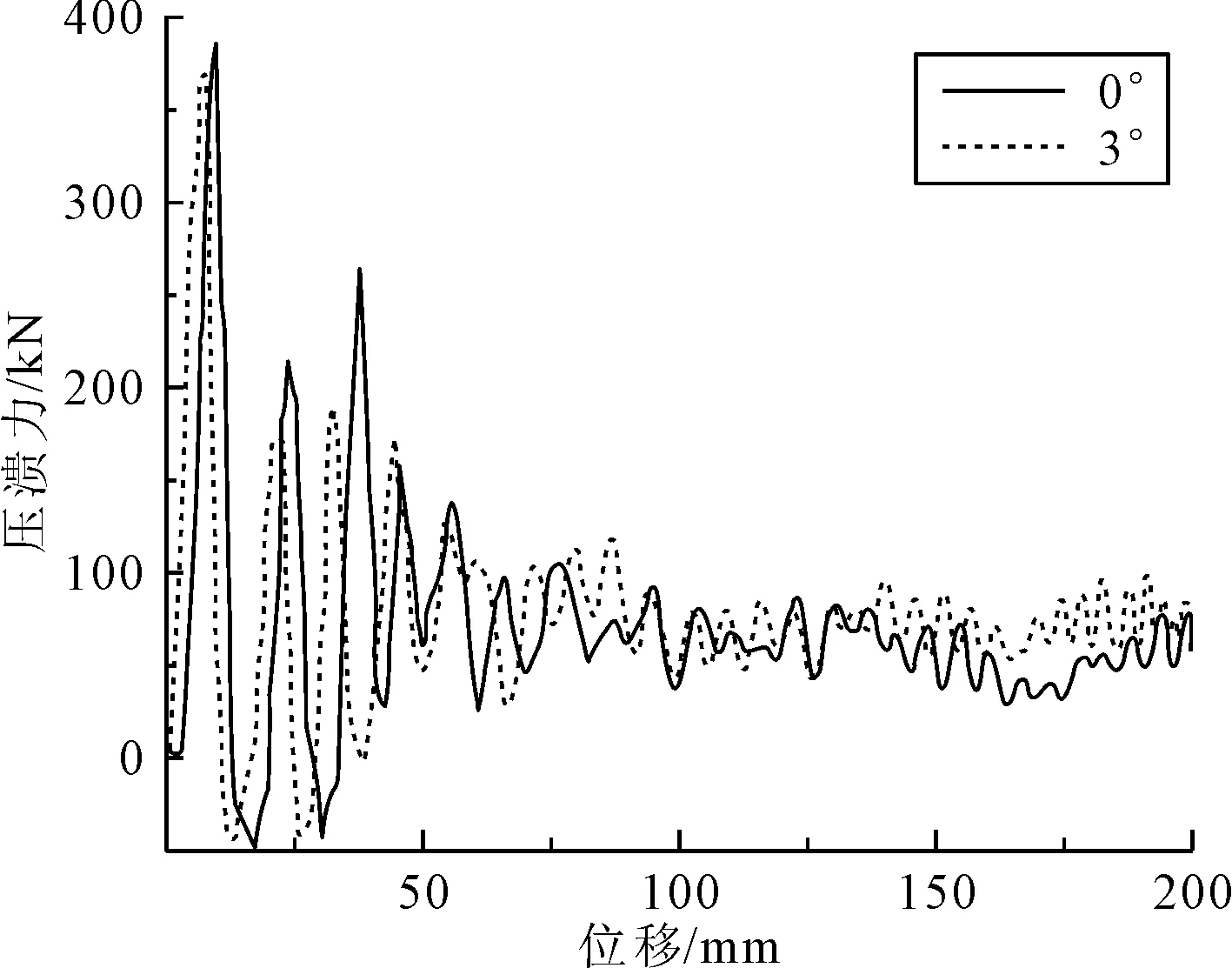
图11 0°和3°样件轴向冲击位移-压溃力曲线

4 结论

基于仿真分析与动态落锤试验，笔者对焊接翻边轴向冲击下双帽形薄壁梁吸能特性的影响进行了研究，得到以下结论：①焊接翻边的增加可有效改善双帽形薄壁梁的变形形式，提高压溃力与SEA值；②对称斜向焊接边的设计对提高平均压溃力及改善变形模式有显著效果；③落锤冲击试验表明，所建立的仿真分析模型具有较高的可信度，对称斜向焊接边的倾斜角度设计合理有效。

[1] 余同希,邱信明.冲击动力学[M].北京：清华大学出版社,2011:120-122.

[2] LIU Y C. Crashworthiness design of multi-corner thin-walled columns[J]. Thin-walled Structures, 2008, 46(12)：1329-1337.

[3] LIU Y C. Crashworthiness design of thin-walled curved beams with box and channel cross sections[J]. International Journal of Crashworthiness, 2010, 15(4): 413-423.

[4] 余同希,卢国兴.材料与结构的能量吸收[M].北京：化学工业出版社,2006:45-50.

[5] JENSEN Q, LANGSETH M, HOPPERSTAD O S. Experimental investigations on the behaviour of short to long square aluminium tubes subjected to axial loading[J]. International Journal of Impact Engineering, 2004, 30(8): 973-1003.

[6] ABRAMOWICZ W, WIERZBICKI T. Axial crushing of multicorner sheet metal columns[J]. Journal of Applied Mechanics, 1989, 56(1): 113-120.

[7] 孙凌玉,姚迎宪.车身薄壁梁结构轻量化设计的理论研究[J].北京航空航天大学学报,2005,30(12):1163-1167.

[8] KUMAGAI K, HAYASHI S, OHNO T. Rupture modeling of spot welds under dynamic loading for car crash FE analysis[J]. Transactions-society of Automotive Engineers of Japan, 2007, 38(5): 9-11.

[9] NAGEL G M, THAMBIRATNAM D P. A numerical study on the impact response and energy absorption of tapered thin-walled tubes[J]. International Journal of Mechanical Sciences, 2004, 46(2): 201-216.

[10] HOU S, LI Q, LONG S, et al. Design optimization of regular hexagonal thin-walled columns with crashworthiness criteria[J]. Finite Elements in Analysis and Design, 2007, 43(6): 555-565.

WANG Feng:Doctorial Candidate; School of Mechanical and Electronic Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

Effect of Welded Flange on Energy Absorption of Spot-weld Double-hat Section

WANGFeng,MOYimin,LVJuncheng,HUANGFeng,LINZhigui

Spot-weld double-hat section is the main structural form selection of automobile and ship safety collision. The effects of width and new shape of spot-weld on thin-walled beam energy absorption characteristics were investigated through the simulation analysis. Results of drop hammer experiment show that the crushing force and SEA can be significantly increased by the width increasing and new shape of spot-weld.

spot-weld double-hat section; welded flange; axial dynamic impact; energy absorption

2015-05-05.

王峰(1985-)，男，宁夏银川人，武汉理工大学机电工程学院博士研究生.

2095-3852(2015)06-0715-05

A

F407.472；TB12

10.3963/j.issn.2095-3852.2015.06.012