一类修正的双组份Dullin-Gottwald-Holm方程组解的爆破现象

杨 露，郭真华

(1.西北大学 数学学院; 2.西北大学 非线性中心, 陕西 西安 710069)



·数理科学·

一类修正的双组份Dullin-Gottwald-Holm方程组解的爆破现象

杨 露1,2，郭真华1,2

(1.西北大学 数学学院; 2.西北大学 非线性中心, 陕西 西安 710069)

为研究一类修正的双组份DGH方程组的爆破现象，首先对该方程组的守恒量进行先验估计; 然后研究了周期情形和非周期情形下, 给初值赋予一些条件, 得到的一些新的爆破结果。

修正的双组份DGH方程组;周期情形和非周期情形;爆破

本文研究下面修正的双组份DGH方程组的Cauchy问题[1-3]:

(1)

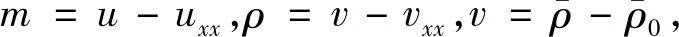
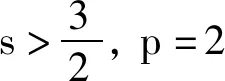
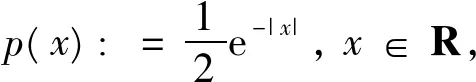
(3)

1 预备知识

为了文章的完整性,在这一部分将引入一些基本的定理和引理,由于证明过程类似,故省略其证明。利用文献[7]的证明方法可得定理1。

类似于文献[11]中定理4.1和定理4.2的证明,得到如下两个定理。

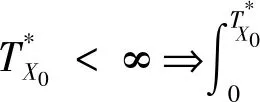
(4)

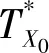
考虑引入两类特征线[10]:

(5)

和

(6)

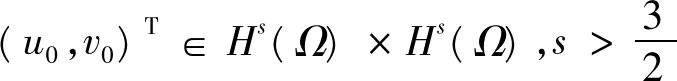
qi,tx(t,x)=ux(t,qi(t,x))qi,x(t,x),i=1,2。

进一步积分得到

这表示对任意的t∈[0,T),qi,x(t,·): R→R (i=1, 2)是两个微分同胚。

2 爆破现象

接下来的问题就是如果解只有在有限时间内存在的话, 那么当解爆破的时候它又有什么特点呢? 所以寻找一些充分条件尤其是初始值的充分条件来保证解在有限时间内爆破就显得尤为重要。

2.1 非周期区域的爆破现象

在这一部分, 我们研究在非周期区域里解的爆破情况, 并通过改进得到一些新的爆破准则。

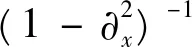
(7)

为了简化后文中的表示式，记

(8)

下面介绍一个非常有用的引理,它揭示了方程(1)的能量守恒律。

∀t∈[0,T)。

(9)

证 明 证明E(t)关于时间变量是守恒量。

由注1知, 最大存在期限T不依赖初值u0的正则性指标s的选取, 故不妨设s≥3。 在方程(1)的第1个方程两边同时乘以u(x,t)并且分部积分, 得到

(10)

同样地, 对于方程(1)的第2个方程有如下的性质:

(11)

进一步计算得到

(12)

式(10)和(11)表明

(13)

因此,E(t)是守恒量。 证毕。

结合上述引理2以及Sobolev不等式, 得到

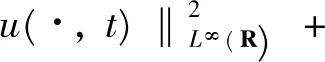
其中上式对任意的t∈[0,T)均成立。这表明u与v是有界的。

受文献[12]启发, 下面是本文得到的第一个爆破结果。

若满足

M(0)<

那么u(x,t)在有限时间内爆破。

证 明 结合稠密性定理以及文献[12]的论证思想来获得本定理的证明。 我们仅需要证明当s≥3时该定理成立。 本定理证明s=3的情况。

对方程(3)两边同时关于x求导, 有

(14)

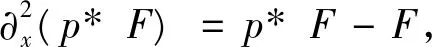
(15)

进行简单的计算, 有

(16)

式(16)的计算用到下面的性质

综上所述, 得到关于M(t)的方程

(17)

运用式(8),式(17)变形为

(18)

式(18)以及以下性质运用了引理1,

(19)

利用引理2得到的u与v的最大模估计，得到

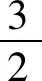
另一方面, 有Cauchy-Schwartz不等式

(20)

综合上述一系列分析, 可得

本定理的假设和关于Riccati型方程的标准讨论可以保证存在T,使得

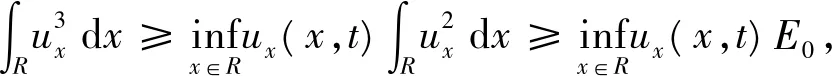
证毕。

类似于文献[14],得到如下结果。

(21)

那么方程(3)对应于初值X0的最大存在期限T是有限的, 即解爆破。

证 明 由式(15)可知

则对于几乎处处(0,T)上,函数n(t)满足方程

(22)

进而在点(ξ(t),t)处, 得到

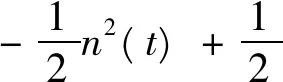
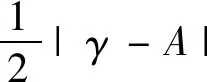
|γ-A|‖u‖L∞(R)≤

(23)

上述式(23)第1步运用了引理1。

容易证明若满足条件(21),上述Riccati型方程的解n(t)在有限时间内趋于-∞。

受到文献[10]启发, 接下来是本文得到的关于爆破现象的一个主要定理。

m0(x0)=0,

(24)

且

(25)

那么方程(3)对应于初值X0的最大存在期限T是有限的, 即解爆破。

证 明 因为对于任意的t∈[0,T),由式(6)定义的q2(t,·)是实直线之间的一个微分同胚, 则存在一点x(t)∈R, 使得

q2(t,x3(t))=q1(t,x0),t∈[0,T)。

(26)

当t=0时,有

x3(0)=q2(0,x3(0))=q1(0,x0)=x0。

(27)

首先证明

ρ(t,q1(t,x0))=0,

(28)

m(t,q1(t,x0))=0

(29)

对于任意的t∈[0,T)均成立。

事实上,由方程(3)第2个方程可以推知

-ux(t,q2(t,x3(t)))ρ(t,q2(t,x3(t)))，

由于ρ0(x0)=0, 对上式积分并且运用式(27), 得到

ρ(t,q2(t,x3(t)))=

即ρ(t,q1(t,x0))=ρ(t,q2(t,x3(t)))=0, 对于任意的t∈[0,T)均成立。

另一方面, 结合式(5)和(28)以及方程(3)第一个方程, 可以推知

进而可知, 对于任意的t∈[0,T), 有m(t,q1(t,x0))=0。

为简单起见,下文将用q1来代替q1(t,x0)。

定义V(t)=ux(t,q1(t,x0)), ∀t∈[0,T),沿着轨道q1(t,x0), 运用式(28)与引理1,同时注意本定理条件γ=A, 式(15)可变形为

本文想要证明对任意的t∈[0,T),V(t)是严格递减的, 即上式右边是严格小于0。 为达到这个目的，需要证明下面的论断。

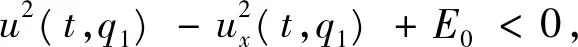
证 明 用反证法证明该论断。 若上述论断的结论不成立, 则存在一个t0，使得有

而

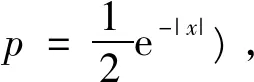
进一步得到其微分形式

为了证明该论断,现在考虑在点(t,q1(t,x0)),令

经过简单的计算可得

(30)

式(30)右边第1部分表明

结合方程(2)的第一个方程, 式(30)右边第2部分表明

(v-vxx)vx)dξ=

运用下面的关系式

m(t,q1)=0=u(t,q1)-uxx(t,q1),

进而得到

因此结合上述一系列计算以及本论断的假设, 式(30)变形为

这表明当t∈[0,t0)时I(t)是严格递增的。 由连续性可知

(31)

类似于I(t)的证明,可以得到

因此由连续性可以保证

(32)

结合式(31)与(32), 得到

显然矛盾。 因此有

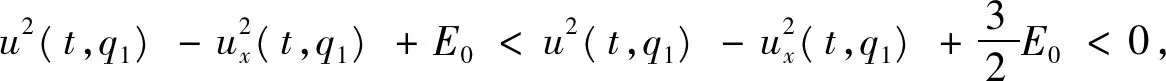
所以V(t)=ux(t,q1(t,x0))是严格递减的。 另一方面,

ux(t,q1(t,x0))=

论断得证。

直接计算解上述不等式得

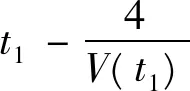
2.2 周期区域的爆破现象

在这一部分, 考虑周期区域上的爆破现象。 令S:=R/Z表示单位圆, 接下来将在S:=R/Z上进行讨论, 即函数u(x,t)与v(x,t)要满足

u(x,t)=u(x+1,t),v(x,t)=v(x+1,t), ∀t∈[0,T)。

注意到本部分中对任意的函数f∈L2(S), 引入

其中[x]表示x的整数部分。容易推出

(33)

定义卷积运算

通过直接计算可以得到‖p‖L∞(S)=C1(C1在后文中出现)。 我们将在本部分中描述周期区域与非周期区域爆破情况的不同。 受文献[14-15]启发, 得到以下定理。

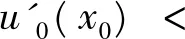
其中

那么方程(1)对应于初值X0的解在有限时间内爆破。

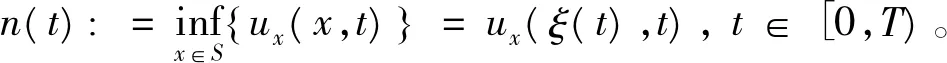
由文献[16]推出如下形式Sobolev不等式

(34)

其中C0≈0.869<1是卷积问题(34)的最优常数。 类似于在非周期区域情形下引理1的计算, 有

(35)

然而在S上, 卷积问题(34)无法精确找到最优常数(详见文献[16])。

文献[11]证明了

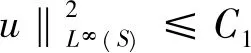
(36)

结合上述计算可得

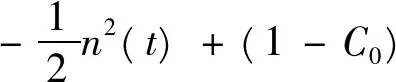
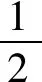
|γ-A|‖p‖L∞(S)‖u‖L1(S)+

|γ-A|‖u‖L∞(S)≤

因此, 定理的条件保证了方程(1)对应于初值X0的解在有限时间内爆破。 证毕。

类似于文献[14-15]的论证思想, 我们得到下面的定理。

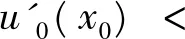
其中常数C0与C1定义如上,且

那么方程(1)对应于初值X0的解在有限时间内爆破。

证 明 本定理会为方程(1)的解作出新的范数估计。

现运用文献[17]中得到的已知结果, 即对任意函数f∈H1(S), 有

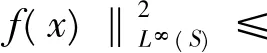
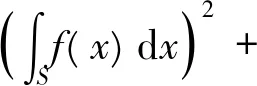
对u(x,t)运用上式的结果可得

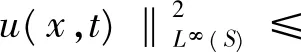
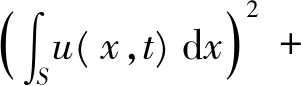
综合上述计算, 容易得到

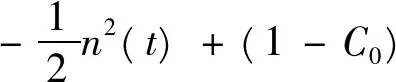
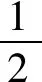
|γ-A|‖p‖L∞(S)‖u‖L1(S)+

|γ-A|‖u‖L∞(S)≤

|γ-A|2(1+C1|S|)}K0+

因此, 定理的条件保证了方程(1)对应于初值X0的解在有限时间内爆破。 证毕。

类似于文献[14], 我们得到本文中最后一个爆破结果。

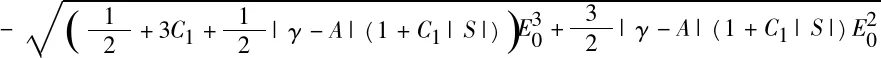
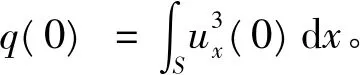
因此, 定理的条件保证了方程(1)对应于初值X0的解在有限时间内爆破。 证毕。

[1]GUOZ,ZHUM.Wavebreakingforamodifiedtwo-componentCamassa-Holmsystem[J].JDifferEquations,2012, 252: 2759-2770.

[2]JINL,GUOZ.Anoteonamodifiedtwo-componentCamassa-Holmsystem[J].NonlinearAnalRealWorldAppl,2012, 13: 887-892.

[3]HOLMD,TRONCIC.Singularsolutionsofamodifiedtwo-componentCamassa-Holmequation[J].PhysRev,2009,79(3)：101-125.

[4]CONSTANTINA,ESCHERJ.Ontheblow-uprateandtheblow-upofbreakingwavesforashallowwaterequation[J].MathZ, 2000, 233: 75-91.

[5]TIANL,GUIG,LIUY.OntheWell-posednessproblemandthescatteringproblemfortheDullin-Gottwald-Holmequation[J].CommunMathPhys, 2005, 257: 667-701.

[6]FUY,QUC.Wellposednessandblow-upsolutionforanewcoupledCamassa-Holmequationswithpeakons[J].JMathPhys,2009, 50: 012906.

[7]GUIG,LIUY.OntheCauchyproblemforthetwo-componentCamassa-Holmsystem[J].MatZ, 2011, 268: 45-66.

[8]WUS,YINZ.Globalexistenceandblow-upphenomenafortheweaklydissipativeCamassa-Holmequation[J].JDifferentialEquations,2009, 246: 4309-4321.

[9]GUANC,YINZ.Globalexistenceandblow-upphenomenaforanintegrabletwo-componentCamassa-Holmshallowwatersystem[J].JDifferentialEquations,2010, 248: 2003-2014.

[10]GUOF,GAOH,LIUY.Onthewave-breakingphenomenaforthetwo-componentDullin-Gottwald-Holmsystem[J].JLondMathSoc,2012, 86: 810-834.

[11]GUIG,LIUY.Ontheglobalexistenceandwave-breakingcriteriaforthetwo-componentCamassa-Holmsystem[J].JFunctAnal,2010, 258: 4251-4278.

[12]CONSTANTINA.Well-posedness,globalexistence,andblowupphenomenaforaperiodicquasi-linearhyperbolicequation.Comm[J].PureApplMath,1998, 51: 475-504.

[13]CONSTANTINA,ESCHERJ.Wavebreakingfornonlinearnonlocalshallowwaterequations[J].ActaMath,1998(1)：229-243.

[14]GUOZ,JINL,NIL.Blowupcriteriaofsolutionsforamodifiedtwo-componenthyperelasticrodsystem[J].JournalofMathematicalPhysics,2012，13(2)：887-892.

[15]HUQ,YINZ.Globalexistenceandblow-upphenomenaforaperiodic2-componentCamassa-Holmequation[J].MonatsheftefürMathematik,2012, 165: 217-235.

[16]ZHOUY.Blow-upofsolutionstoanonlineardispersiverodequation[J].CalculusVarPartialDifferEqu,2006, 25:63-77.

[17]ZHOUY.Wavebreakingforaperiodicshallowwaterequation[J].JMathAnalAppl,2004, 290: 591-604.

[18]ZHOUY,GUOZ.BlowupandpropagationspeedofsolutionstotheDGHequation[J].DiscreteContinDynSystSer,2009, 12: 657-670.

(编 辑亢小玉)

Blow-up criteria of solutions for a class of modified 2-component Dullin-Gottwald-Holm system

YANG Lu1,2, GUO Zhen-hua1,2

(1.School of Mathematics, Northwest University; 2.Center for Nonlinear Studies, Northwest University, Xi′an 710069， China)

This paper introduces the wave breaking phenomenon of a modified two-component DGH equations. Firstly, a prior estimate for the modified two-component DGH equations was studied. Then some new blow-up criteria were established for this system formulated either on the line or with space-periodic initial condition.

a modified two-component DGH system; real line and the periodic case; blow-up criteria

2014-03-11

国家自然科学基金资助项目(11071195, 11331005)

杨露，女，山西长治人， 从事偏微分方程的研究。

O175.2

：ADOI：10.16152/j.cnki.xdxbzr.2015-02-002