Cantor集的结构及应用

阮世华

(莆田学院 数学学院，福建 莆田 351100)

Cantor集的结构及应用

阮世华

(莆田学院 数学学院，福建 莆田 351100)

Cantor集是实函数论中一类重要的集合.本文从Cantor集的构造过程以及构造拓展中得到相关的应用.目的是帮助初学者对Cantor集有一个较全面的认识.

Cantor集；结构；完备集

Cantor三分集是Cantor在解三角级数问题时做出来的，它具有若干重要特征，常是我们构造重要特例的基础.

1 Cantor三分集[1]

2 Cantor集构造法的拓展

在[0,1]中做出总长度为δ(0<δ<1是任意给定的数)的稠密开集.为此，取p=(1+2δ)/δ，并采用类似于Cantor集的构造过程：第一步，我们移去长度为1/p的同心开区间；第二步，在留存的两个闭区间的每一个中，又移去长度为1/p2的同心开区间；第三步，在留存的四个闭区间中再移去长度为1/p3的同心开区间；…….继续此过程，可得一列移去的开区间，记其并集为G(开集)，则G的总长度为δ.我们称Cp=[0,1]G为类Cantor集[2](当p=3时，Cp就是Cantor三分集)Cp也是非空完备集，且没有内点.

更一般的，已有文献[3]对[0,1]做相关的构造，所得到的点集也具有Cantor三分集完全相同的奇特性质，这里我们就不详述.

3 Cantor集构造拓展后的应用

例1 证明：用十进制小数表示[0,1]中的数时，其用不着数字6和7的一切数也是完备集.

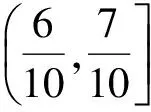
例2 证明：用十进制小数表示[0,1]中的数时，其用不着数字5和7的一切数成一完备集.

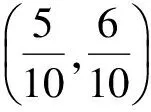
一般的，用十进制小数表示(0,1)中的数时，其用不着数字a1和a2的一切数成一完备集，其中a1，a2是1,2…9中的数字.

例3[2]设

an=2或7},

我们有

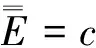
证：①若有{xm}⊂E:xm→x(m→∞)，则

如果|xm-x|<10-p，那么在xm∈E时bn=2或7(n=1,2,…，p-1)，从而E是闭集.

③由于E∩(0.28,0.7)=φ，故E在[0,1]中不稠密.

例4[2]试作一个由无理数构成的完备集.

[1]程其襄，张奠宙，魏国强,等.实变函数与泛函分析基础[M].3版.北京：高等教育出版社，2010.

[2]周民强.实变函数论[M].2版.北京：北京大学出版社，2008.

[3]董大校.Cantor集的性质及其构造推广[J].JournalofYunnanFinance&EconomicsUniversity,2008,23(5)：95-96.

[4]江泽坚，吴智泉，纪友清.实变函数论[M].3版.北京：高等教育出版社，2007.

[责任编辑：Z]

The Structure and Applications of Cantor Set

RUAN Shi-hua

(Department of Mathematics, Putian University, Putian Fujian 351100, China )

Cantor set is an important set in real functions theory. This paper studies the applications through the construction process and generalized structure of cantor set. The aim of this paper is to help the beginners to have a general understanding of it.

Cantor set; structure; complete set

2015-03-10

阮世华(1977-)，女，福建莆田人，讲师，主要从事研究方向为多复变函数研究。

O

A

1671-5330(2015)05-0141-02