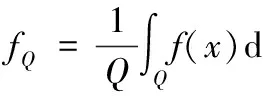Schrödinger型算子与新BMO函数的交换子的极大算子在L空间上的一个估计
2015-02-16白莉红
白莉红
(甘肃建筑职业技术学院 基础课部,甘肃 兰州 730050)
Schrödinger型算子与新BMO函数的交换子的极大算子在L空间上的一个估计
白莉红
(甘肃建筑职业技术学院 基础课部,甘肃 兰州 730050)
二进 Sharp 极大函数定义为
Schrödinger 算子;交换子;反向 Hölder 不等式;Sharp 极大函数:BMOV(Rd)
1 引言及结果
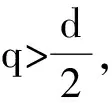
(1.1)
把满足 (1.1) 式的函数的集合记作RHq. 与Schrödinger算子L相关的算子半群定义为
Tt,f(x)=e-tLf(x)=∫Rdkt(x,y)f(y)dy,f∈L2(Rd),t>0.
(1.2)
其中 kt(x,y)为r-tL的核.
我们首先给出一些记号和定义.
(1.3)
易知 ρ(x)>0, 且对任意 x∈Rd,ρ(x)≥0有限[4]. 关于ρ(x), 我们有下面估计.
命题1[5]存在常数c和k0≥1 , 使得对x,y∈Rd, 成立
(1.4)
特别地,当y∈Br(x), 且r≤ρ(x)时,有ρ(x)~ρ(y).
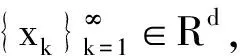
(i)∪kQk=Rd;
(ii)存在N=N(ρ), 使得每一k≥1, 有card{j:4Qj∩4Qk≠Ø}≤N,其中Qk:={|x-xk|<ρ(xk)}.
定义1 BMOV(Rd)空间定义为:
-fB|dx<∞.
(1.6)
显然有BMO(Rd)⊂BMOV(Rd), 当V=0或α=0时,BMO(Rd)=BMOV(Rd)若存在常数C0>1使得任意球B*⊂2B, 有
ψ(B*)≤A0ψ(B)
(1.7)
则称ψ满足D∞条件.
(a) T 可扩展为L2(Rn)上的有界线性算子.
(c) 核K(x,y)满足Calderon-Zygmund估计:
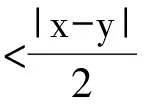
(1.8)
(1.9)
(1.10)
在证Lp有界性的过程当中C-Z算子的光滑条件(1.9)起了重要的作用.但由于位势V的缘故这里的核不具有这样的光滑条件,但我们可以通过另外一种光滑性条件来证明Lp有界性.
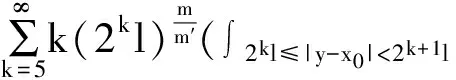
定义4 二进Sharp极大函数定义为
本文主要结果如下:
定理 设 T 是 C-Z 算子,对任意s>1, 有
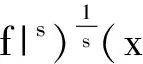
2 定理的证明
为证明定理, 需要以下引理:
引理1[5]假设V∈RHq, 则有
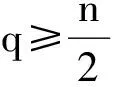
‖(-Δ+V)-1Vf‖p≤Cp‖f‖p;
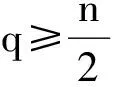
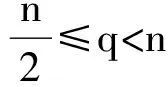
对p0'≤p<∞,有
记Γ(x,y,τ)是Schrödinger算子
-Δ+(V(x)+iτ),τ∈R的基本解. Γ0(x,y,τ)是算子-Δ+iτ,τ∈R的基本解.易知Γ(x,y,τ)=Γ(y,x,-τ), 关于Γ(x,y,τ)有以下引理:
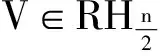
Γ(x,y,τ)≤
其中Ck是与x,y,τ无关的常数.
引理4[5]假设V∈RHq0,q0>1,假设对某x0∈Rn,R>0,在B(x0,2R)上成立
-Δu+(V(x)+iτ)u=0.
则有
(i)对x∈B(x0,R),
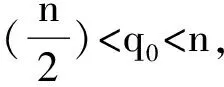
(∫B(x0,2R)|
命题3 令m>1, 假设对∀p∈(m′,∞),T是Lp有界的,K满足Hm条件, 则∀b∈BMOV,[b,T]是Lp有界的, 且
‖[b,Tf]‖p≤Cp‖b‖BMOV‖f‖p
定理的证明:对任意的λ, 有[b,T]f(x)=(b(x)-λ)Tf(x)-T((b-λ)f)(x)
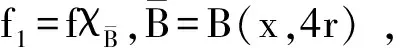
-T((b-λ)f)(y)-D|dy
=I+II+III
≤Cψ(B)‖b‖BMOVMr(Tf)(x).
对于II, 利用Kolmogorov不等式得
≤Cψ(B)‖b‖BMOVMr(f)(x).
-bB(x,2k+1)||f(ω)|dω
-bb(x,2k+1)|∫B(x,2k+1)|f(ω)|dω
≤Cψ(B)‖b‖BMOVMs(f)(x).
由于ψ(B)<1, 由极大函数的性质得
≤C‖b‖BMQVMs(f)(x)
+C‖b‖BMQVMs(Tf)(x).
对于第二部分, 由Hölder不等式和Kolmogorov不等式得:
-T((b-λ)f)(y)|dy
≤C‖b‖BMOV(Ms(Tf)(x)+Ms(f)(x)).
综上得
定理证毕.
[1]Dziubański J, Zienkiewicz J. Hardy space H′ assocoiated to Schrädinger operators with potential satisfying reverse Hälder inequality[J]. Rev. Math. Iberoam., 1999, 15(2):279-296.
[2]Dziubański J, Zienkiewicz J. Hpspaces assocoiated with Schrädinger operators with potentials from reverse Hälder classes[J]. Colloq. Math., 2003, 98(1):5-38.
[3]Dziubański J, Garrigós G, Martínez T, Torrea J, Zienkiewicz J. BMO spaces related to Schr?dinger operators with potentials satisfying a reverse H?lder inequality [J]. Math. Z., 2005, 249(2):329-356.
[4]Bongioannia B, Harbour E, Salinasa O. Weighted inequalities for negative powers of Schrädinger operators~[J]. J. Math. Anal. Appl., 2008, 348(1):12-27.
[5]Shen Z V. LPestimate for Schrädinger operators with certain potentials [J]. Ann. Inst. Fourier, 1995, 45(2):513-546.
[6]Zhong J., Harmonic analysis for some Schrädinger operators [D], Ph.D.Thesis, Priceton University, 1993.
[责任编辑:Z]
L Estimate for Maximal Operators of Commutators Associated to Schrödinger and New BMO Functions
BAI Li-hong
(Gansu Institute of Architectural Technology, Lanzhou 730050, China)
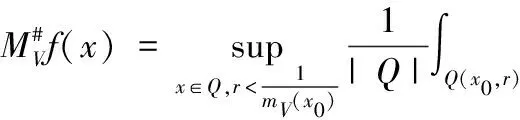
Schrödinger operators; Commutators; Reverse Hölder iequality; Sharp maximal function;BMOV(Rd)
2015-05-10
2014年甘肃省高等学校科研资助项目(2014A-142)
白莉红(1978—), 女, 甘肃张掖市人,讲师,主要研究方向为调和分析。
O
A
1671-5330(2015)05-0010-04