钢管结构中T型节点平面内抗弯刚度分析
2015-02-15陈俊岭
陈俊岭, 黄 皇
(同济大学 建筑工程系,上海 200092)
0 引言
钢管桁架因便于制作、外形美观,在室外过街天桥、展览馆等建筑物中广泛应用。空腹钢管桁架由上下弦杆和竖腹杆组成,因没有斜腹杆外形更加简洁,因此越来越受到建筑师的青睐。空腹钢管桁架的受力不同于普通钢管桁架,更多地表现出梁的受力特性——以弯曲变形为主,同时承受轴力、弯矩和剪力。一般而言,带有斜腹杆的钢管桁架节点假定为铰接,按空间或平面桁架体系进行内力计算;但空腹钢管桁架则不同,计算时必须考虑腹杆与弦杆交界处节点的抗弯刚度,否则结构体系不成立。空腹钢管桁架一般采用直接相贯焊节点,连接方便、用钢量省,但节点处的抗弯刚度对整体结构的受力性能影响很大[1]。以某过街天桥空腹桁架立柱中T 型相贯节点为对象,研究了对相贯焊节点平面内抗弯刚度有较大影响的重要参数,通过有限元计算结果与国内外规范相关计算公式的比较,验证了各个公式在本例中的适用性,最后给出了判断节点是刚接还是半刚接的计算方法。

图1 空腹桁架(单位:mm)
1 T型相贯节点的平面内抗弯刚度
某实际工程的过街天桥柱采用图1 所示空腹桁架柱,弦杆为Φ351/25钢管,腹杆为Φ152/20钢管,构件之间采用直接相贯焊的连接方式。根据《钢管结构技术规程》CECS280—2010[2]第5.1.4条规定,当桁架平面内杆件的节间长度或杆件长度与截面高度(或直径)之比不小于12(主管)和24(支管)时宜按铰接节点模型计算桁架内力,否则按刚接计算。本工程中节间长度与主管截面高度之比为2.71,与支管截面高度之比为5.26,远远小于上述规定,因此应按刚接节点对整体结构进行内力计算,但是本工程中空腹桁架采用直接相贯的连接方式,节点区域又未设置加劲板,节点的抗弯刚度是否满足刚接节点的要求尚值得商榷。
在实际工程中以空腹钢管桁架作为承重柱时,虽然杆件仍以受压为主、按构件边缘屈服确定其极限承载力,但桁架节点区域有次弯矩影响,且在加载初期构件处于弹性小变形状态,可忽略杆件内力对节点初始转动刚度的影响,故把弦杆(主管)与腹杆(支管)的无量纲化几何特征参数作为节点初始刚度的主要影响因素。由于作用在节点域的荷载将导致主管管壁的弯曲,因此节点域的局部变形主要取决于相贯面周围主管管壁的弯曲刚度[3],单位宽度壳的弯曲刚度可表达为

式中,T 为壳的厚度;υ为泊松比;E 为弹性模量。
因此,影响T 型节点转动刚度的因素主要为弦杆壁厚以及影响简化力偶臂大小的参数,即弦杆的径厚比γ、腹杆与弦杆的直径比β、腹杆与弦杆的壁厚比τ,具体含义为γ =D/(2T),β=d/D,τ=t/T。其中D和T 分别为弦杆的直径和厚度,d 和t分别为腹杆的直径和厚度(见图2)。控制D 为不变量,则其他参数确定后,节点的几何特征即可确定。
节点的刚度是指引起节点区域单位局部变形所需要的力,通常取节点的力-变形曲线上的第一加载步的力与变形的比值,或取曲线中接近直线的前几步(如前3步)加载步的力与变形比值的平均值近似为节点初始刚度。根据节点域局部变形的不同获取方法,可以将相贯节点的刚度定义分为两种:直接法和间接法[4]。本文采用直接法计算抗弯刚度,即不考虑支管变形对节点局部转角φ 的影响,相贯线附近的主管管壁视为节点域,认为节点局部转动完全由相贯线附近主管壁的变形引起,直接在相贯线附近主管管壁设立测点即可获得相关的变形。

图2 结构尺寸以及各参数(单位:mm)
节点的平面内转角φ定义为图2中相贯线冠点1点和2点局部变形(扣除主管作为梁受弯的挠度)差值与两冠点间距的比值,相贯焊节点鞍点3(4)、5(6)点测得位移近似反映弦杆弯曲的挠度,测出以上6个点在x 方向(图2中垂直于主管管轴的方向)的位移,则平面内弯矩引起的节点转角为

式中,Δ1~Δ6为各点在x 方向的位移;d、t分别为支管的直径和厚度。
如图2所示,计算平面内抗弯刚度时,节点所受弯矩M 为荷载P 在支管根部节点相贯面上的冠点处产生的弯矩值。根据有限元分析数据得到节点的平面内转角为φ,则节点的平面内抗弯刚度为KM=M/φ。图2节点中主管为图1空腹桁架柱相邻两节间反弯点之间弦杆,支管为空腹桁架中水平腹杆反弯点至节点之间的部分腹杆的计算模型。

图3 网格划分
2 有限元分析
为研究空腹桁架中T 型直接相贯焊节点的平面内刚度,利用通用有限元软件ANSYS,采用3维4结点弹塑性壳单元SHELL181对节点的极限承载力进行有限元分析。划分网格时,为获取图2中6个点的位移,采取较为规则的网格划分,仅主支管交汇附近网格加密(见图3)。钢管材料为Q345,弹性模量为2.06×105MPa,泊松比为0.3,材料模型为理想弹塑性,钢材屈服强度为345 MPa。分析时考虑材料非线性和几何非线性影响,不考虑节点区焊缝以及残余应力对节点承载力的影响。控制主管外径的值为常量,即D =351mm,为了保证所加荷载符合实际情况以及避免加载点因应力集中导致局部变形过大,在主管和支管的端部设置了刚性板,约束和荷载均加在刚性板上。
表1给出了各个计算模型的几何尺寸,各尺寸模型符合我国现有的无缝钢管的规格,其中参数β、γ、τ分别有5组计算模型进行分析,分析各个参数时其他两个参数保持不变。
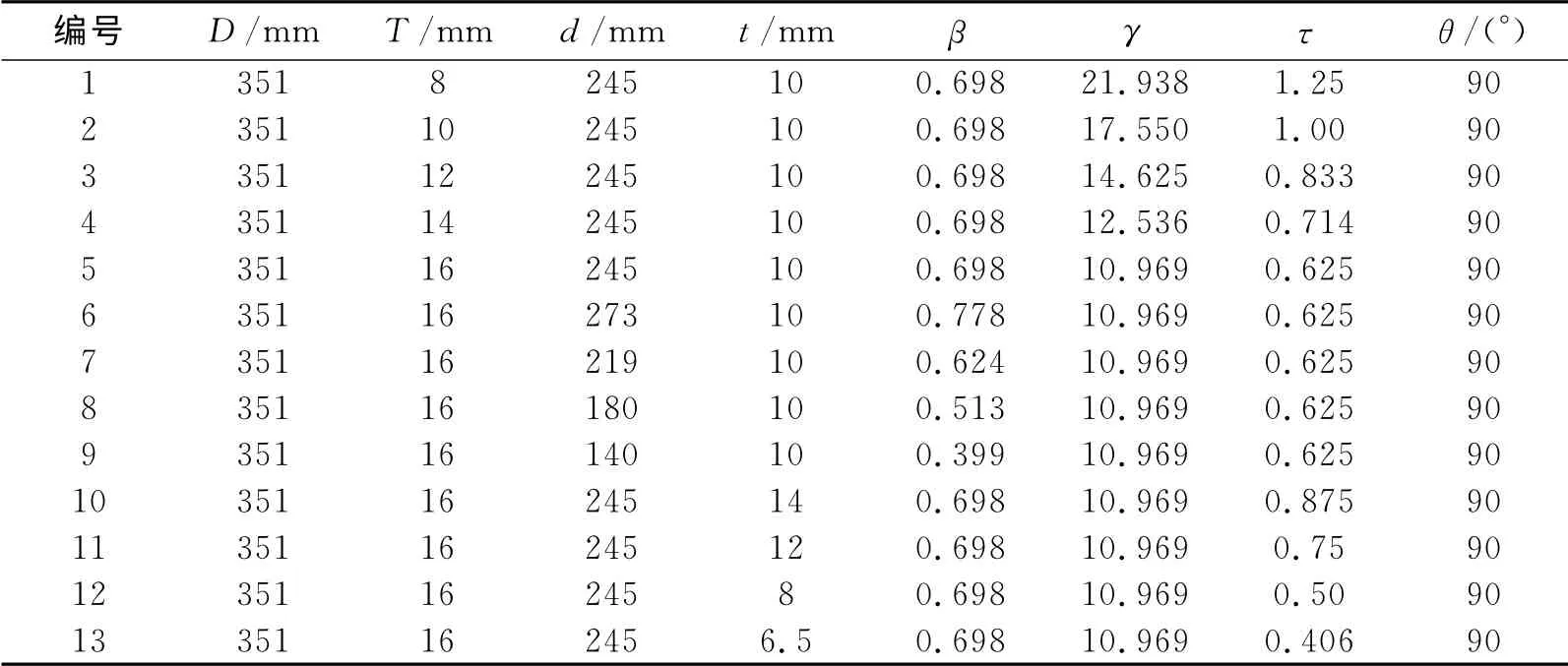
表1 各节点模型的几何参数
2.1 腹杆与弦杆的直径比β的影响
保持主管管径D =351mm、主管壁厚T =16mm、支管壁厚t=10mm 不变,仅变化支管管径d计算,通过ANSYS有限元分析得到不同β值的M-φ曲线(图4)。当β较小时,整个节点以局部变形为主,主要表现为主管壁在与支管连接处向内部凹陷。当β增大时,腹杆直径d增大,则简化力偶间的力臂增大,此时若弯矩不变则力偶值减小,导致冠点局部变形减小,所以相贯面转角减小,即节点刚度增大[5],此时节点的变形表现为主管壁在与支管连接处向内部凹陷的同时,侧面逐渐向外突出。从图4可以看出,不同β值对相贯节点平面内转动刚度的影响。
2.2 弦杆的径厚比γ 的影响
保持主管管径D =351mm、支管管径d=245mm,支管壁厚t=10mm 不变,仅变化主管壁厚T 进行计算,通过Ansys有限元分析可以得到不同γ值的M-φ曲线(图5)。在弦杆直径保持不变的情况下,当γ增大时,弦杆壁厚T 减小,所以相贯面的弯曲刚度减小,导致节点平面内抗弯刚度减小。从图5中可以看出,不同的γ值对平面内转动刚度的影响。

图4 不同β值M-φ 曲线

图5 不同γ值M-φ 曲线
2.3 腹杆与弦杆的壁厚比τ的影响
保持主管管径D =351mm、支管管径d=245mm,主管壁厚T =16mm 不变,仅变化支管壁厚t计算,通过ANSYS有限元分析得到不同τ值的M-φ 曲线(图6)。当τ增大时,腹杆壁厚t增大,由于腹杆直径d 不变,所以简化力偶间的力臂(腹杆壳体中面的直径)略有减小,此时若弯矩不变则力偶值增大,导致冠点局部变形增大[5],所以相贯面转角增大,节点抗弯刚度略有降低但不明显,从图6中可看出,不同的τ值对平面内转动刚度基本没有影响。
各参数对节点抗弯刚度的影响关系曲线见图7,从图7中可以看出,β和γ 对节点抗弯刚度影响较大,参数τ对节点刚度影响不明显。
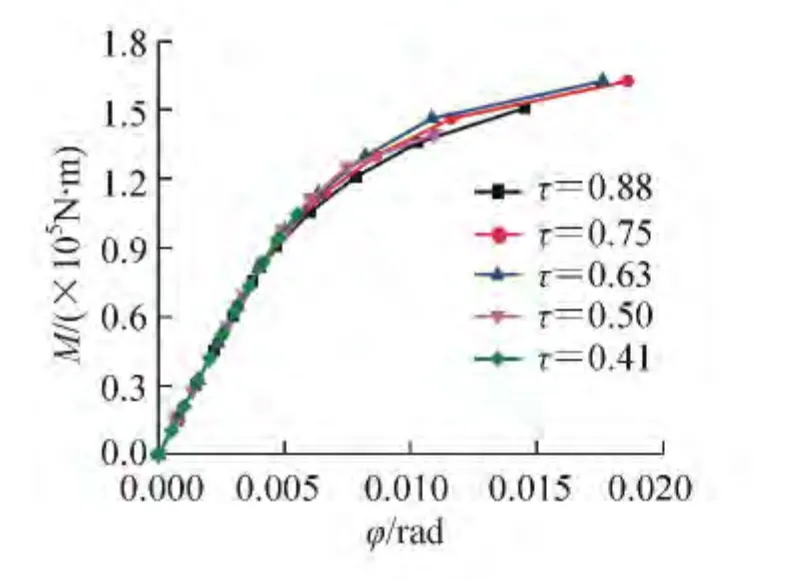
图6 不同τ值M-φ 曲线
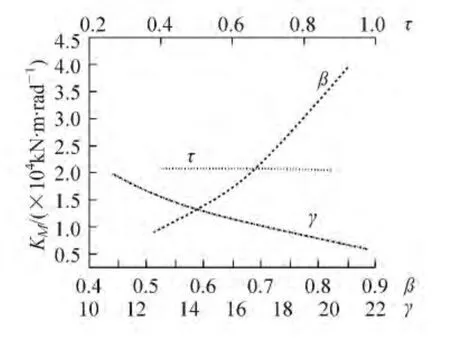
图7 各参数对抗弯刚度的影响分析
3 有限元计算结果与现有计算公式对比
现有的相贯焊节点转动刚度计算公式主要来自于模型计算和试验数据分析,虽然大多数计算公式建立在试验数据的基础上,但试验数据同样有局限性。由于试验成本和加载设备的限制,使得试验数据不可能覆盖工程节点实际尺寸的全部范围;尽管试件客观上包含了材料、制作、构造特性等多种影响,但难以将这些因素定量地区别出来[6]。
目前,应用较广泛的是DNV 规程[7],当弦杆的径厚比γ和腹杆与弦杆的直径比β满足一定条件时,在海洋工程钢结构设计部分中给出了T 型相贯焊节点平面内抗弯刚度计算方法(见式(3))。有限元数值分析结果与式(3)计算结果对比如图8所示。从图8可以看出,除个别数据外,DNV 规程计算结果比ANSYS有限元分析结果普遍稍小。
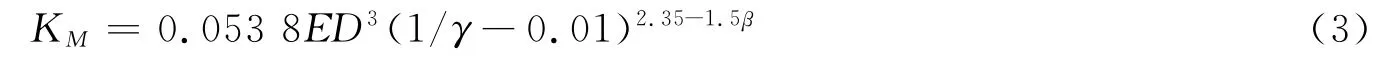
式中,0.33 ≤β ≤0.8;10 ≤γ ≤30。
Fessler[8]曾采用环氧树脂(弹性模量约为钢材的1/60)制作T 型节点模拟T 型钢管节点试验,控制直径D =132mm 为固定值,得到27个不同的节点模型的柔度矩阵,并根据其柔度矩阵获得了T、Y 型节点的抗弯刚度参数计算公式,见式(4)。有限元数值分析结果与式(4)计算结果对比如图9所示。

图8 DNV规程与数值计算结果对比

图9 Fessler公式与数值计算结果对比

式中,0.3≤β ≤0.8;10 ≤γ ≤20;30°≤θ ≤90°。
从图9可以看出,按Fessler给出的计算公式所得结果普遍大于ANSYS有限元分析结果,误差多数在10%~20%之间,个别模型达到28%。主要原因可能是由于试验采用环氧树脂模拟钢材,在弹性阶段,简单的按照弹性模量的相似关系分析试验结果可以接受,但材料一旦进入塑性,由于二者材性的差异,两种材料间不具备简单的相似关系。
我国《钢管结构技术规程》[2]给出平面T 形受弯矩作用的节点承载力计算公式,但并未给出节点抗弯刚度的计算公式。王伟等[9]将有限元分析结果经多元线性回归分析及数理统计检验,最终拟合得到
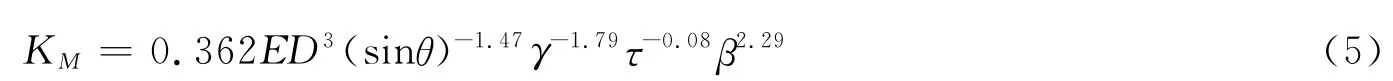
式中,30°≤θ ≤90°;0.2 ≤β ≤1.0;10 ≤γ ≤50;0.2 ≤τ ≤1.0。
不同于DNV 规程公式和Fessler给出的计算公式,公式(5)考虑了支管壁厚t与主管壁厚T 的比值τ的影响。从图10可以看出,本文有限元数值分析结果与公式(5)计算结果吻合较好。
4 节点刚度
通过有限元数值分析可以得到T 型节点平面内抗弯刚度KM,但是由于实际工程中空腹桁架多采用杆系结构进行内力分析,节点连接处一般简化为理想的刚接、铰接或者介于二者之间的半刚接。理论上,理想的刚接节点的平面内抗弯刚度应无限大,理想的铰接节点的抗弯刚度为零,但这两种理想状态在实际工程中不可能存在,一般根据节点处的弯矩-转角曲线具体判别。我国现行规范和欧洲规范均未给出空腹钢管桁架节点刚度的具体判别方法,欧洲规范EC3[10]提出结构在正常使用条件下,按抗弯刚度对钢框架梁柱节点进行分类时,认为节点承载力在理想刚性连接承载力的95%以上,即是刚性连接。文献[11]则认为节点对转角位移的转动约束能力在理想刚接的95%以上时即可认为是刚接。
本文采用文献[11]刚性节点的判别方法,即利用T 型节点半刚接时端截面A 的转角位移δs与刚接时端截面A 的转角位移δr(如图11所示),按式(6)计算空腹钢管桁架T 型节点的约束转动能力,当Δ ≤0.05时,即可以认为是刚接。


图10 王伟公式与数值计算对比

图11 刚接与半刚接计算模型
在正常使用极限状态下,构件一般处于线弹性工作状态,可按式(7)求得半刚接的转角位移。当KM→∞时,即可以由式(7)求得刚接节点的转角位移


式中,kb=EIb/lb,kc=EIc/lc分别为支管与主管的线刚度。将式(7)和式(8)代入式(6),可得

由此可见,当节点的抗弯刚度KM与支管线刚度之比满足式(9)时,即可认为节点为刚接,节点的转动刚度和主管线刚度、支管线刚度以及二者的比值有关。按上述方法计算表1中各节点的抗弯刚度与支管线刚度之比可得表2中结果。
根据《钢管结构技术规程》第5.1.4条规定,所有的节点模型都应该为刚接,但表2中可见,由于编号为1、2、3模型主管的管壁较薄,由式(1)可得管壁单位宽度壳的弯曲刚度减小,同时主管的线刚度也减小,节点的抗弯刚度KM与支管线刚度之比不满足式(9),节点应看作半刚性节点。所以从严格意义上讲,《钢管结构技术规程》第5.1.4条简单利用节间长度与管径的比值判断并不准确。

表2 各节点模型抗弯刚度KM 与支管线刚度之比
5 结论
以空腹桁架立柱中T 型相贯节点为研究对象,采用有限元软件对T 型节点的平面内抗弯刚度进行了数值分析,通过与现有计算公式的对比分析,给出T 型节点刚度的判别方法,主要结论如下:
(1)T 型相贯焊节点平面内抗弯刚度随腹杆与弦杆的直径比β的增大而增大,随弦杆的径厚比γ的增大而减小,随腹杆与弦杆的壁厚比τ的增大而稍有减小。
(2)相贯焊T 型节点的转动刚度和主管线刚度、支管线刚度以及二者的比值有关,不能简单的根据节间长度与管径的比值来确定。
[1]王伟.圆钢管相贯节点非刚性性能及对结构整体行为的影响效应[D].上海:同济大学建筑工程系,2005.
[2]中国工程建设协会标准.CECS2802010 钢管结构技术规程[S].北京:中国计划出版社,2011.
[3]吴连元.板壳理论[M].上海:上海交通大学出版社,1989.
[4]赵必大,赵滇生,梁佟.圆钢管相贯节点刚度的两种获取方法及其比较[J].西安建筑科技大学学报,2013,45(1):43-50.
[5]王伟,陈以一.圆钢管相贯节点的非刚性能与计算公式[J].工业建筑,2005,25(11):5-9.
[6]陈以一,陈扬骥.钢管结构相贯节点的研究现状[J].建筑结构,2002,32(7):52-55.
[7]Det Norske Veritas.Rules for the Design,Construction and Inspection of Offshore Structures[S].Det Norske Veritas,Oslo Appendix C:Steel Structures,1997.
[8]Fessler H,Mockford P B,Webster J J.Parametric Equations for theFlexibility Matrices of Single Brace Tubular Joints in OffshoreStructures[J].Proc.Instn Civ.Engrs,1986,81:675-696.
[9]王伟,陈以一.圆钢管相贯节点局部刚度的参数公式[J].同济大学学报,2003,31(5):515-519.
[10]CEN.Eurocode3:Design of steel structures,Part 1-8:Design of joint[S].London:[s.n.],2005.
[11]Goto Y,Miyashita S.Classification system for beam-to-Column connection[J].Structure Engineering,1998,124:750-757.
