滑坡变形预测灰色神经网络耦合模型的构建及适用性分析

高彩云 崔希民

1 中国矿业大学（北京）地球科学与测绘工程学院，北京市学院路丁11号，100083

2 河南城建学院测绘工程学院，平顶山市明月路，467044

3 矿山空间信息技术国家测绘地理信息局重点实验室，焦作市世纪大道2001号，454000

众多学者借助灰色模型和神经网络对滑坡变形进行预测研究［1－6］。实践证明，利用灰色GM（1，1）模型进行滑坡体变形预测所需建模样本信息量少、计算简单，能较好地弱化滑坡体变形序列的随机性，挖掘滑坡系统的演化规律，但对具有明显波动特性的滑坡样本数据预测效果较差。而神经网络较强的非线性映射能力能较好地描述数据序列中的波动特性，将灰色GM（1，1）模型和神经网络（artificial neural network，ANN）技术进行融合，建立灰色神经网络耦合模型。本文从系统论观点出发，结合岩土体流变理论和时序分析原理，提出基于滑坡变形时序分解的串联式、基于模型信息综合利用的并联式和基于算法融合的混联式3类灰色神经网络耦合模型，并对其适用性进行讨论。

1 典型滑坡位移模式及状态辨识

典型滑坡变形时序可以分为4类［1，7］（图1）。图1（a）为凸形曲线，位移随时间推移而增加，最终趋于稳定，位移变化速率由减速逐渐转入近似匀速；图1（b）为凹形曲线，滑坡位移在前期增速不明显，在后期急剧增加，变化速率由近似匀速短时间内转为增速；图1（c）、图1（d）为凸、凹曲线的复合，演化规律较为复杂，预测难度较大，故本文将其作为主要研究对象。

图1 典型滑坡位移时序曲线Fig.1 Typical curves of landslide time series

2 滑坡变形预测GM 与ANN的互补性研究

灰色系统和神经网络建模原理有较大的差异，但两者存有如下互补性［1－8］：

1）灰色系统理论不适合对非线性变化数据的逼近，而ANN 的优势在于能以任意精度对非线性变化的数据进行逼近。

2）ANN 虽然具有逼近非线性函数的能力，但前提条件是需要足够多的隐含层节点数量，而节点数量的增加会导致ANN 参数增多，相应地需要大量建模样本数量。在短期滑坡变形预测中，较容易获得大量监测值，但在中长期预测中，滑坡体监测样本数量相对减少，而GM 则可以利用较少的样本进行建模预测。

3）ANN 进行滑坡预测时，需确定相应的激励函数，通常采用Sigmoid 函数。Sigmoid 函数是一类单调增长的函数，GM 通过累加生成削弱滑坡随机性干扰，累加生成序列呈单调递增趋势，比较适合采用ANN 进行逼近。

3 滑坡变形预测GM－ANN 耦合模型的构建

根据GM 和ANN 模型对滑坡变形数据处理的特点，将灰色神经网络模型分为3类：1）基于滑坡变形位移时序分解的串联式（series grey artificial neural network，SGANN）；2）基于滑坡变形模型信息综合利用的并联式（parallel grey artificial neural network，PGANN）；3）基于算法融合的混联式（inlaid grey artificial neural network，IGANN）。

3.1 串联式GM－ANN

根据系统理论和时序分析原理，滑坡变形位移可用如下响应成分模型表示：

式中，Yt为滑坡变形位移，Ut为位移的趋势项，Vt为具有不确定性的随机项。

结合已有的研究成果和滑体蠕变特征［5－6］，Ut可以利用GM 模型进行较好的描述，能充分发挥灰色系统理论对滑坡监测显信息和隐信息的利用；Vt为一复杂的非线性序列，这里采用神经网络对其进行描述。基于滑坡变形位移时序分解的串联式GM－ANN 建模流程如图2所示。

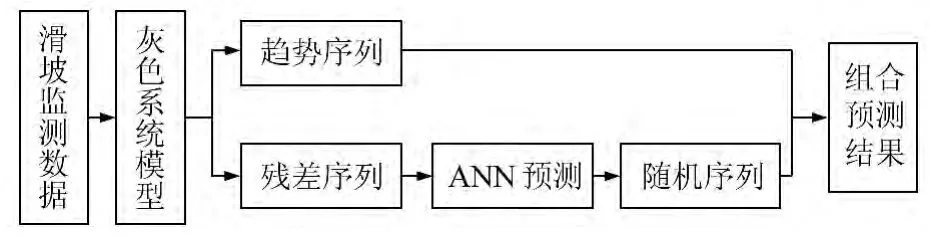
图2 串联式灰色神经网络模型流程图Fig.2 Flow chart of constructing SGANN model

3.2 并联式GM－ANN

并联式GM－ANN 预测模型的基本思路是：对滑坡位移模式及状态辨识后，分别用GM（1，1）和神经网络对滑坡变形进行预测，然后对两种模型预测结果进行适当组合作为实际预测值，其原理如图3所示。

图3 并联式灰色神经网络模型流程图Fig.3 Flow chart of constructing PGANN model

PGANN 模型的实质是权重约束下的组合预测，其目的在于综合利用灰色GM（1，1）和ANN所提供的信息，从而避免单一模型丢失信息的缺陷，提高滑坡变形预测精度。由图3 可知，对于PGANN 组合，单项预测模型权重的大小将直接影响组合预测的精度。文献［9］证实基于神经网络的智能非线性定权法具有较高的预测精度，故本文在PGANN 模型建立过程中，采用该方法定权。

3.3 混联式GM－ANN

混联式GM－ANN 的构建借鉴了灰色系统理论对神经网络拓扑结构的优化改造，旨在强化神经网络对滑坡数据的处理能力，提高ANN 的运算效率、增强鲁棒性等。提出两种形式的混联模型：基于灰处理的混联型GM－ANN（a类）；基于灰色模型群的混联型GM－ANN（b 类）。两种混联模型流程图如图4、图5所示。

图4 a类混联式灰色神经网络模型流程图Fig.4 Flow chart of constructing IGANN model（a type）

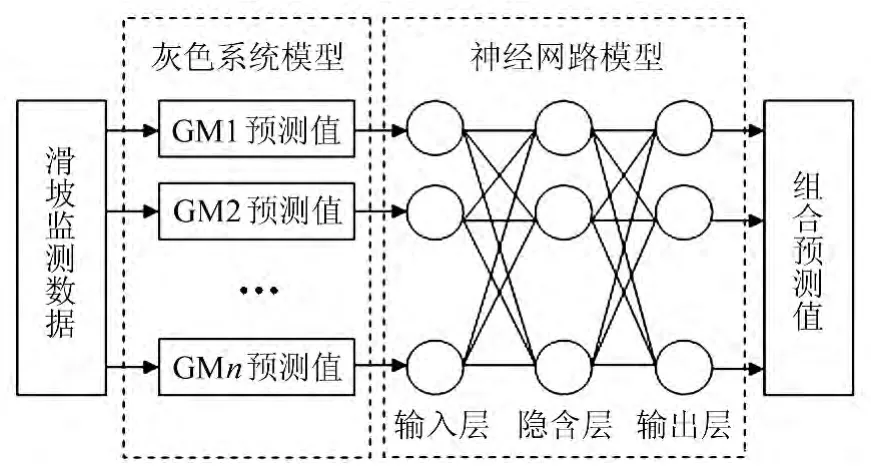
图5 b类混联式灰色神经网络模型流程图Fig.5 Flow chart of constructing IGANN model（b type）

a类混联GM－ANN 在神经网络输入时增加一个灰色累加层，其作用是将滑坡变形监测值利用灰色一次累加1－AGO（accumulation generating operation）生成技术弱化原始数据的随机性。经AGO 处理后的原始数据为单调递增序列，且具有类指数变化规律，有利于发挥神经网络的非线性拟合能力，提高网络学习效率和收敛度。神经网络学习训练后，在输出时经累减还原处理（1－IAGO）得到IGANN 滑坡组合预测值。

b类混联GM－ANN 通过灰色系统模型（可采用传统灰色、残差修正、新陈代谢、背景值修正和初始值修正等模型）处理后得到一簇顾及不同影响因素下的灰色模型群（GM1、GM2、…、GMn），模型群的变化区间反映了不同影响因素下灰色GM 模型对影响因素的响应，利用神经网络非线性逼近能力对灰色模型群进一步逼近，从而得到组合预测值。

4 算例分析

为验证本文3类灰色神经网络耦合模型在滑坡动态预测中的可行性，并与单一灰色模型、神经网络预测效果进行比较，利用沪蓉高速公路施工中的古树屋段滑坡体［10］主滑方向3号监测点33期监测数据进行建模计算（1～28期建模，29～33期预测），采用最大相对误差、最小相对误差、平均相对误差和误差均方根4个指标衡量模型预测性能。滑坡监测数据曲线见图6。由图6结合图1，对古树屋段滑坡体进行位移模式及状态辨识，认为其演变过程属于复合型滑坡。

图6 古树屋滑坡位移实测曲线Fig.6 Curves of Gushuwu landslide monitored

3类灰色神经网络耦合模型构建过程中，需选取合适的神经网络模型。本文结合已有的研究成果并考虑智能算法的发展趋势，选取极限学习机（extreme learning machine，ELM）作为神经网络模型。该算法以广义逆（moore penrose，MP）和欧氏空间为基础，与传统算法相比，在训练过程中输入层和隐含层间的连接权值及隐含层阈值随机产生，无需调整，只需设置隐含层神经元节点数便可获取全局最优解，学习速度快，网络泛化能力强。

4.1 灰色神经网络耦合模型的建立

1）SGANN 的建立。按§3.1 建立SGANN组合预测模型，选取GM（1，1）的建模序列长度为4，采用等维滚动建模提取滑坡变形趋势项（图7（a））。利用ELM 算法训练随机项，即训练样本为GM（1，1）残差项，采用3维数等维滚动训练，其拓扑结构3－18－1。隐含层神经元激励函数为Sigmoid函数，输出层1个节点，逼近效果见图7（b），SGANN 组合预测效果见图7（c）。

2）PGANN 的建立。利用文献［9］的神经网络非线性定权方法建立PGANN 组合模型，GM（1，1）的建模序列长度为4，采用等维滚动建模，单一模型ELM 网络拓扑结构3－7－1。对两单一模型预测值进行非线性并联组合时，网络输入数据为GM（1，1）和ELM 预测结果，网络目标输出为滑坡监测值，神经网络拓扑结构3－3－1。单一模型及非线性并联组合预测结果见表1。

图7 滑坡变形监测值与SGANN 模型预测值的关系曲线Fig.7 Relation curves of landslide monitored and predicted deformation

3）IGANN 的建立。a类混联GM－ANN：训练样本为灰色处理后的归一化数据，采用3维滚动建模进行训练，其网络拓扑结构为3－7－1，组合预测效果见图8。b类混联GM－ANN：建立基于不同维数（从4维、8维、12维逐一递增至28维）的灰色模型群，模型群预测值作为神经网络输入，滑坡监测值作为目标输出，神经元数量为300，组合预测效果见图9。

图8 滑坡变形监测值与a类IGANN 模型预测值关系曲线Fig.8 Relation curves of landslide monitored and a－IGANN model predicted deformation

图9 b类IGANN 模型预测曲线Fig.9 Relation curves of landslide monitored and b－IGANN model predicted deformation

4.2 灰色神经网络耦合模型的预测效果剖析

表1列出了单一模型及3类灰色神经网络耦合模型的预测结果，结合实验对其进行剖析。

1）对于单一模型而言，GM（1，1）、ELM 模型预测精度相当，但GM（1，1）模型通过连续滚动预测方法，不断建立新的预测模型，计算量大，而ELM 算法建模简单方便、无需迭代计算，具有较好的非线性逼近能力。

2）SGANN 模型结合滑坡监测数据的特点，从数据分解角度出发，兼顾数据的趋势性与随机性，建模过程中极大利用了数据的有效信息，取得了较好的预测效果，适用于复杂滑坡变形数据的处理。

3）PGANN 以GM（1，1）、ELM 模型为基础，其预测效果受单一模型预测精度和权重系数的影响。该组合模型以神经网络非线性智能动态定权为约束，包含了两类单一模型中所具有的有效信息，具有较高的预测精度。

4）两类IGANN 模型建模机理不同，故在预测方面具有较大的差异。a类IGANN 模型通过灰色累加处理，在一定程度上削弱了原始监测数据的随机性；b类IGANN 模型利用GM（1，1）模型群的有效信息，构建了更为稳定可靠的预测模型，但建模过程复杂、计算量大。

5）对于复杂数据的处理，灰色神经网络耦合模型的预测精度均优于单一模型。

6）从3类灰色神经网络耦合模型预测过程来看，SGANN、PGANN、混联b 类均优于混联a类，其原因是前3者均最大程度地挖掘了滑坡变形监测的有效信息，而混联a类经过累加处理后虽然有利于ELM 的非线性逼近，但丢失了对原始监测数据波动项的利用。

表1 6种模型预测效果比较Tab.1 Comparison of forecasting result among six models

5 结 语

本文针对复合型滑坡位移时序预测，构建了SGANN、PGANN、IGANN 3类灰色神经网络耦合模型。试验表明，SGANN、PGANN、b 类IGANN 进行滑坡预测时可避免采用单一模型对信息利用不充分的缺陷，a类IGANN 在提高预测精度的同时可加快神经网络的收敛。

［1］张军，刘祖强，邓小川，等.滑坡监测分析预报的非线性理论和方法［M］.北京：中国水利水电出版社，2010（Zhang Jun，Liu Zuqiang，Deng Xiaochuan，et al.Landslide Deformation Monitoring Analysis and Prediction Based on Nonlinear Theory and Mothod［M］.Beijing：China Water ＆Power Press，2010）

［2］陈明东，王兰生.边坡变形破坏的灰色预报方法［A］∥全国第三次工程地质大会论文选集［M］.成都：成都科技大学出版社，1988（Chen Mingdong，Wang Lansheng.Grey Model Applied to Slope Deformation and Failure［A］∥Proceedings of the Third Congress of Chinese Engineering Geology［M］.Chengdu：Chengdu University of Science and Technology Press，1988）

［3］唐天国，万星，刘浩吾.高边坡安全监测的改进GM 模型预测研究［J］.岩石力学与工程学报，2005，24（2）：307－312（Tang Tianguo，Wan Xing，Liu Haowu.Improved GM Model for Safety Monitoring of High Rock Slopes［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（2）：307－312）

［4］高宁，高彩云.危岩体变形位移预测的灰色双重优化模型［J］.测绘科学，2014，39（4）：74－77（Gao Ning，Gao Caiyun.Optimized Grey Model for Forecast on Deformation of Dangerous Rock［J］.Science of Surveying and Mapping，2014，39（4）：74－77）

［5］吴益平，滕伟福，李亚伟.灰色－神经网络模型在滑坡变形预测中的应用［J］.岩石力学与工程学报，2007，26（3）：632－636（Wu Yiping，Teng Weifu，Li Yawei.Application of Grey Neural Network Model to Landslide Deformation Prediction［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（3）：632－636）

［6］曹洋兵，晏鄂川，谢良甫.考虑环境变量作用的滑坡变形动态灰色－进化神经网络预测研究［J］.岩土力学，2012，33（3）：847－852（Cao Yangbing，Yan Echuan，Xie Liangfu.Study of Landslide Deformation Prediction Based on Gray Model－Evolutionary Neural Network Model Considering Function of Environmental Variables［J］.Rock and Soil Mechanics，2012，33（3）：847－852）

［7］高宁.贫信息小样本条件下时空动态变形预报方法研究［D］.北京：中国矿业大学（北京），2013（Gao Ning.Research on Forecasting Method of Spatiotemporal Dynamic Deformation under the Condition of Poor Information and Small Sample Data Set［D］.Beijing：China University of Mining and Technology（Beijing），2013）

［8］董辉，傅鹤林，冷伍明.滑坡位移时序预测的核函数构造［J］.岩土力学，2008，29（4）：1 087－1 092（Dong Hui，Fu Helin，Leng Wuming.Kernel Design for Displacement Time Series of Landslide［J］.Rock and Soil Mechanics，2008，29（4）：1 087－1 092）

［9］高彩云，崔希民，高宁.顾及不同约束准则的变形并联组合预测模型研究［J］.大地测量与地球动力学，2014，34（3）：91－94（Gao Caiyun，Cui Ximin，Gao Ning.Study on Deformation Parallel Combination Prediction under Different Restriction Criterion［J］.Journal of Geodesy and Geodynamics，2014，34（3）：91－94）

［10］马文涛.基于灰色最小二乘支持向量机的边坡位移预测［J］.岩土力学，2010，31（5）：1 670－1 674（Ma Wentao.Forecasting Slope Displacements Based on Grey Least Square Support Vector Machines［J］.Rock and Soil Mechanics，2010，31（5）：1 670－1 674）