基于主成分分析的相对重力观测零漂和固体潮提取

于红娟 郭金运，2 李九龙 穆大鹏 孔巧丽，2

1 山东科技大学测绘科学与工程学院，青岛市前湾港路579号，266590

2 海岛（礁）测绘技术国家测绘地理信息局重点实验室，青岛市前湾港路579号，266590

3 中国科学院测量与地球物理研究所，武汉市徐东大街340号，430077

本文通过实验，利用主成分分析（principal component analysis，PCA）提取CG－5重力仪［1］静态相对观测的零点漂移和固体潮。将经过固体潮改正的9d观测数据作为原统计量，使用PCA 提取日零漂，并与最小二乘线性拟合值作对比分析，用含有固体潮和零漂影响的观测数据，在进行零点漂移改正的基础上使用PCA 提取固体潮，并与CG－5重力仪内部软件提供的固体潮模型计算值作对比。通过两组实验对比结果来验证本文方法的可靠性和适用性。

1 主成分分析方法

重力观测的主成分分析［2－5］是基于协方差矩阵将重力数据作为原统计变量，通过线性变换得到新变量，新变量之间统计不相关。PCA 的主要目的是通过分离不相关成分提取主要信息并进行数据降维。文中提取的零点漂移和固体潮为主要信息，即信号。主成分分析假设新变量PCAG＝（PCA1，PCA2，…，PCAn）T是由CG－5重力仪观测数据的原统计变量G＝（G1，G2，…，Gn）T经过线性变换得到的，即

式中，E是由重力观测的统计变量G的协方差矩阵计算得到的线性变换矩阵。假设协方差矩阵为ΣG，则它是一个n阶对称阵。通过求解特征根和特征向量，矩阵ΣG可以分解为：

式中，D是对角阵，对角线上的元素λ1≥λ2…≥λn是矩阵ΣG的特征根，同时等于对应重力观测数据主成分的方差，E是由特征向量构成的正交矩阵［3］。因此，可由式（1）得到：

前k个主成分的综合能力以及所包含的重力值信息量可用累积贡献率α表示：

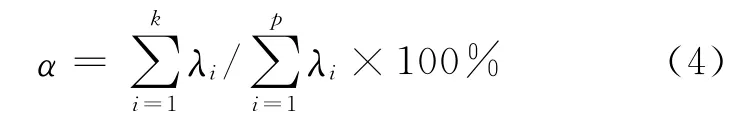
式中，λi表示第i个特征值，p表示特征值总个数，k表示选取的个数。

如果选取较大的k个特征值所对应的新变量重构原重力观测值统计变量，则可以达到提取主要信息的目的［4－5］：

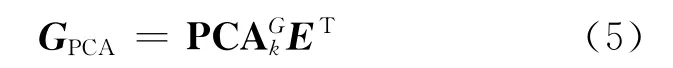
式中，ET表示由选择的特征向量构成的k阶矩阵。

2 数据及预处理

静态相对重力数据由CG－5重力仪（序列号140541221）于某一固定观测站观测9d（2014－08－15～23）所得，以每天09：21至次日09：20为一个时间序列，即作为一个统计观测量。仪器自身具有地震滤波功能，能对低频噪声进行过滤，并舍弃高于6倍标准偏差的高频噪声。采用6 Hz采样率，可对1min的360个样本数据进行平均得到一个读数，观测过程中仪器进行了温度补偿和倾斜改正。因此，每天可以采集同一个时间段（24 h）的1 440个重力观测数据。

把所关心的数据成分认为是信号，其他的作为噪声。假设信号与噪声统计不相关，尝试利用PCA 把这9d的时间序列作为9个统计量来分离信号和噪声。实验使用了两组观测数据，第一组数据是进行了固体潮改正的静态相对观测数据，尝试运用PCA 分离信号和噪声来估算CG－5 重力仪的静态零漂；第二组数据是未进行固体潮改正的静态观测数据，尝试使用PCA 分离信号和噪声来提取固体潮。

由于观测站环境干扰较多，采用滑动平均的方法［6］对数据进行预处理。通过实验并根据重力数据的实际变化情况，选取大小为5的移动窗口进行平滑处理。

3 静态零漂

用第一组数据进行实验，把9d观测数据作为原统计量，使用PCA 将噪声和信号进行分离。每天的数据作为一个统计量，每个统计量为含有1 440×1个元素的列向量，这样9d的观测值就组成了1 440×9 的矩阵，即，。在得到统计量G后，通过式（2）计算其特征向量构成的线性变换矩阵E，再由式（1）得到主成分的9个模式。图1给出了所得到的9个特征根的值，它们等于对应重力观测数据主成分的方差。特征值相对很小甚至接近于0则认为不含有主要的信息，因此，可以从降序排列的特征根中，找到一个特征根来确定主成分的个数，使得剩下的特征根具有接近相同且相对很小的值［4］。从图1可看出，除第一个外其他的特征值都非常小，接近于0。并且通过计算得到第一个模式的贡献率为99.8%，即第一模式包含了几乎所有的数据信息。从图1分析得出，第一模式可以认为是信号部分，而其他8个模式为噪声部分。

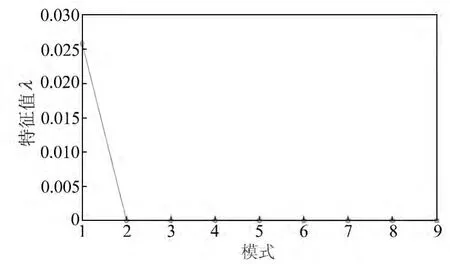
图1 零漂提取中9个模式对应的特征值Fig.1 Eigenvalues corresponding to nine modes in the zero drift estimation

因此，选择第一模式PCA1重构统计量G，分别得到由PCA 估算的9d 的零点漂移。由式（5），选择第一模式进行重构得：

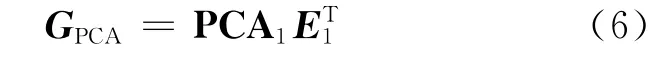
将其展开，得：

表1 08－15～23 零点漂移计算结果Tab.1 Calculated results of daily zero drifts from 08－15to 08－23

从表1可以看出，PCA 与LSLF 的9d日零漂差值均在10－2μGal／d量级，具有非常好的一致性，但是PCA 剔除了噪声，效果更好。因此可以说，PCA 更适用于CG－5静态数据的日漂移常数估算。08－15～23 的日漂移常数有明显增加，说明CG－5 重力仪的零漂具有随时间增加的特点。

4 固体潮

用PCA 得到的日零漂常数对第二组数据进行线性改正，得到经零漂改正但未进行固体潮改正的9d数据，将其作为原统计量并利用主成分分析分离信号和噪声来估算固体潮。每个统计量为含有1 440×1个元素的列向量，这样9d的观测值就组成了1 440×9的矩阵，即

得到统计量G之后，通过式（2）计算其特征向量构成的线性变换矩阵E，再由式（1）得到主成分的9个模式。研究可得，PCA 实现了信号和噪声的分离，图2给出了所得到的9个特征根的值，它们分别等于对应重力数据主成分的方差。

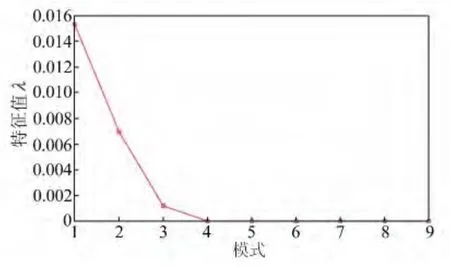
图2 固体潮提取中9个模式对应的特征值Fig.2 Eigenvalues corresponding to nine modes in the solid earth tide estimation

从图2可知，前3个特征值为主要成分［4］。进一步计算得到，第一模式的贡献率为65.2%，前两个模式的累积贡献率为94.8%，前3个模式的累积贡献率为99.9%，几乎包含了重力数据的全部信息。因此，主成分的前3个模式为分离得到的信号，选择该模式来重构统计量G，分别得到PCA 对应的每一个模式的值。图3 给出了线性改正后的9d数据时序图。从图3可见，15和16日的波形变化相近，17～19日的波形变化相近，20～23日的波形变化相近。又因为受固体潮影响，重力观测曲线每天可观测到两个波峰、两个波谷［7］。因此，初步推测波形的不同是这9d的固体潮影响不同所致，并推测这3个模式对应固体潮的变化。通过进一步计算PCA 的前3个模式累积量（见式（9）），即对前3个模式叠加计算并进行中心化处理后的结果（PCA）与CG－5重力仪内部软件提供的固体潮模型计算的固体潮值（solid earth tide，SET）比较发现，3 个模式正好对应于固体潮的影响量。

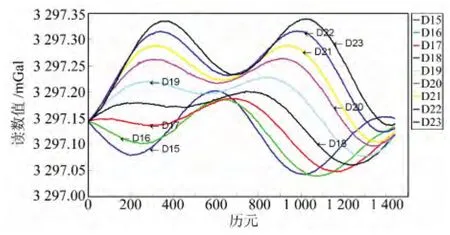
图3 线性漂移改正后的重力数据时序图Fig.3 Gravimetric datatime series of 9days after the linear correction

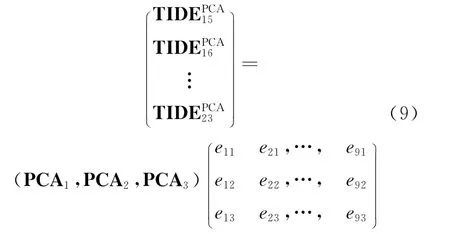
于是，由式（5）选择前3个模式进行重构：

将其展开，得：

从表2看出，PCA和SET计算的固体潮值统计结果中，两者最大差值仅5μGal，具有较好的一致性，说明PCA 可用于静态观测中的固体潮估算。15～23日固体潮的平均值均在0 附近，SET 计算的均值稍微偏离零轴，但整体上正负值具有较好的对称性；15～18日的固体潮高潮值达到90μGal，低潮值达－80μGal；19～23日的固体潮高潮值达124μGal，低潮值达－78μGal。结合图3、图4 可以看出，固体潮具有一定的规律性，每天都会有两个高潮和低潮，并且高潮和低潮会随日期增加往后推迟一段时间。PCA 和SET的均方根和标准差较为接近，相差仅在10－1μGal量级。PCA 和SET 的差值最大均不大于8 μGal，最小都在5μGal内；均值在0附近波动，波动范围在3μGal内；均方根小于5μGal，说明PCA 与SET 计算结果具有很好的一致性。

采用以上计算结果对观测数据进行线性改正和固体潮改正（图5）。CG－5 相对重力仪的重复性标准差为5μGal［1］，而从图5中可以看出，经过改正后的15～23日重力数据变化很小，均在5 μGal范围内。另外，导致这种变化的原因可能还有海潮、零漂的非线性等影响，最后可对数据进行平均得到该测站点的重力读数值。

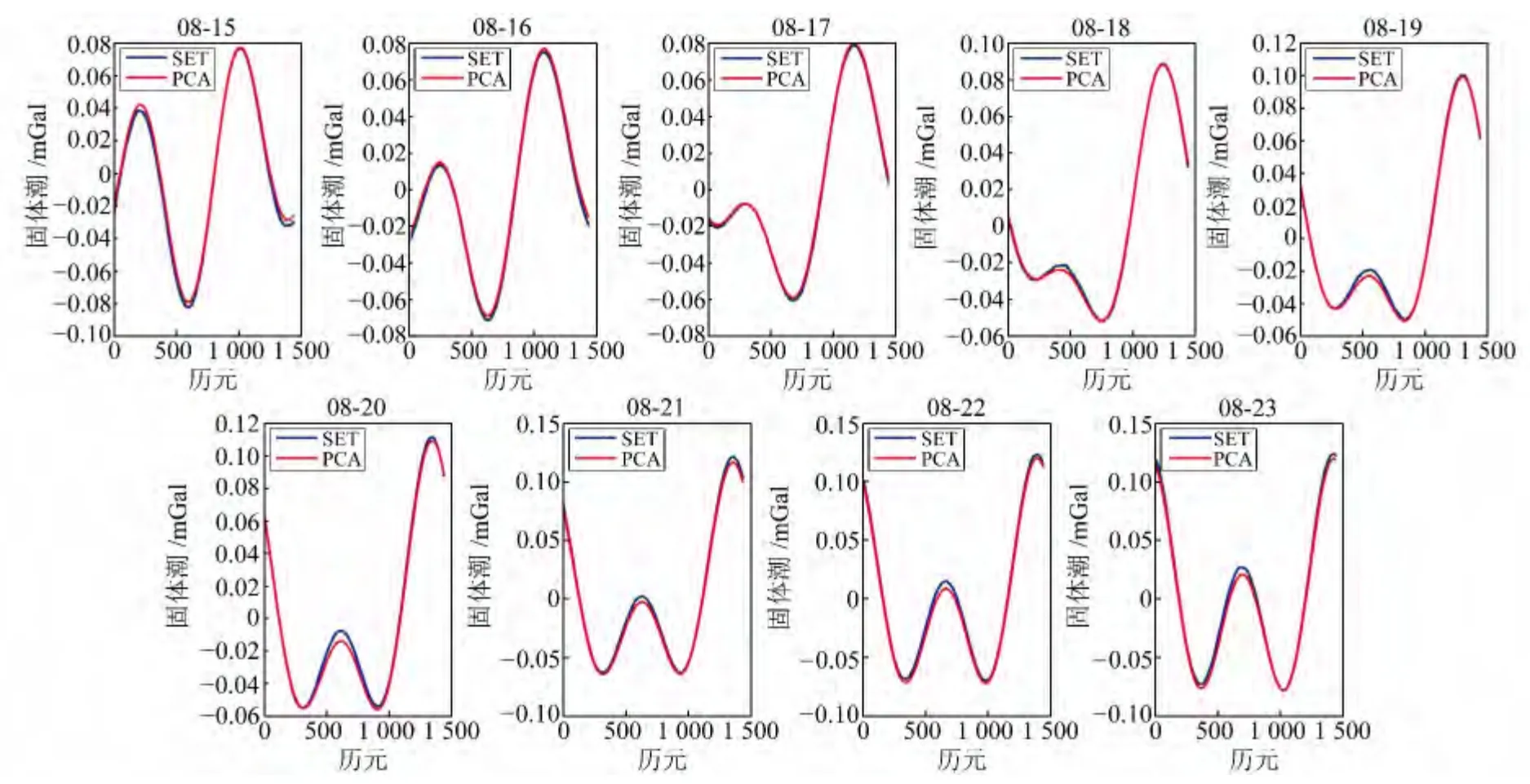
图4 固体潮于08－15～23的PCA 与SET 时序图Fig.4 Time series of the solid Earth tide derived from PCA and SET from 08－15to 08－23

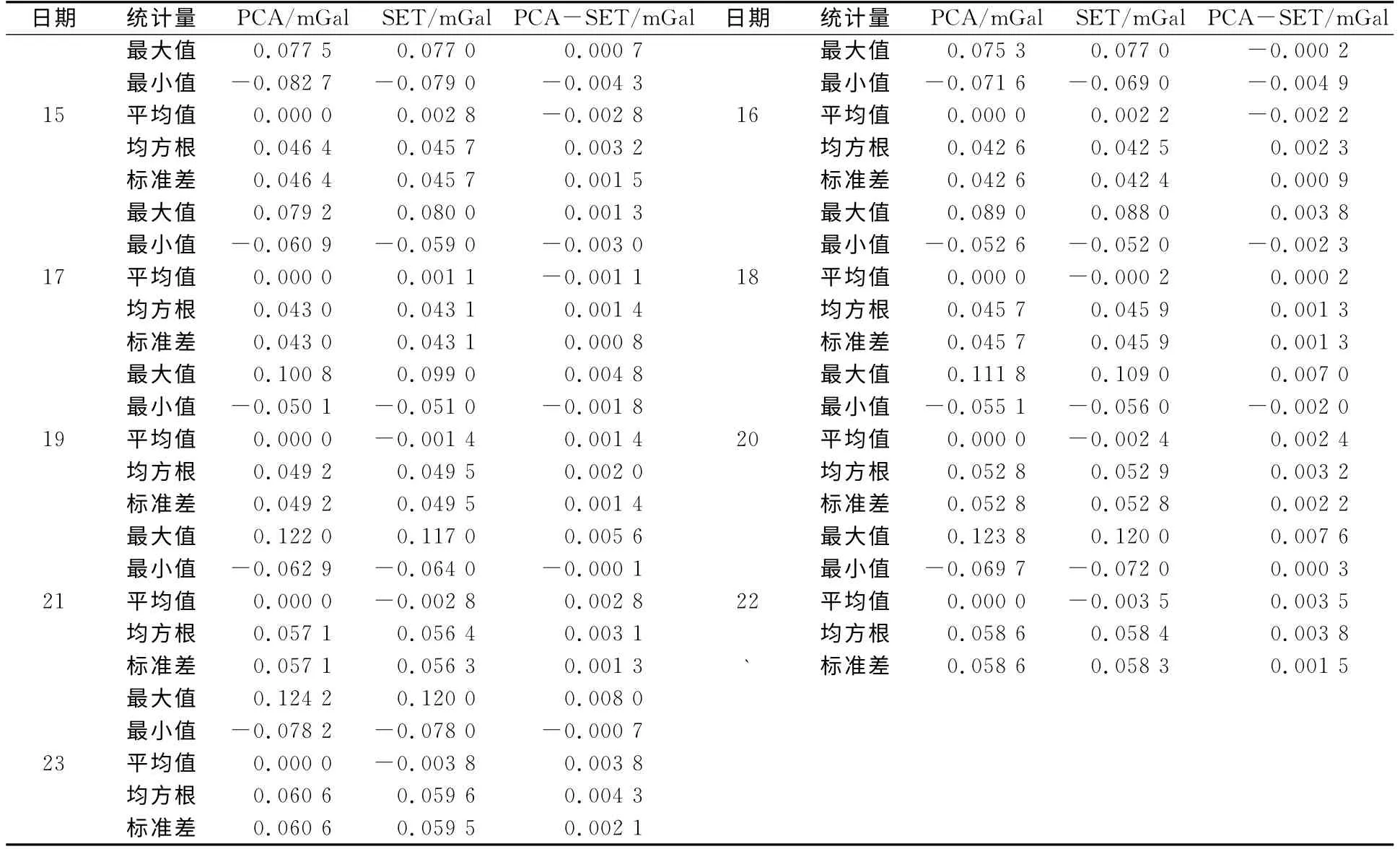
表2 固体潮于08－15～23的PCA与SET统计结果Tab.2 Statistical results of the solid earth tide derived from PCA and SET from 08－15to 08－23

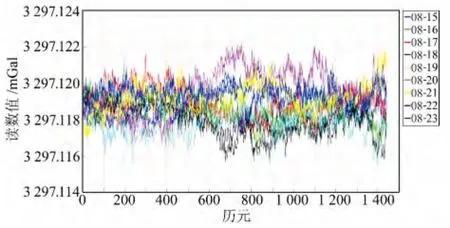
图5 固体潮改正后的重力观测值时序图Fig.5 Gravimetric observations time series after zero drift and solid earth tide correction

5 结 语

1）PCA 提取线性漂移时，第一个模式的贡献率为99.8%，该模式包含了几乎所有数据信息。因此，用该模式估算的线性漂移与LSLF值对比，相差仅在10－2μGal量级，但PCA 剔除了噪声，效果更好。说明在估算零点漂移方面，PCA 比LSLF更具有优越性。

2）PCA 提取固体潮时，第一模式的贡献率为65.2%，前两个模式的累积贡献率为94.8%，前3个模式的累积贡献率达99.9%。可以看出，前3个模式几乎包含了重力数据的全部信息。前3个模式的叠加计算正好对应固体潮，并与SET值基本一致。PCA－SET 的统计值均小于8 μGal，其中均方根都小于5μGal。因此，PCA 用于估算固体潮具有可靠性。

3）根据以上计算结果对观测数据作零漂和固体潮改正后，其变化均在5μGal范围内，导致这种变化的原因可能是仪器的测量精度、海潮和零漂的二次项等微小影响。

［1］Scintrex Limited.CG－5Scintrex Autograv System Operation Manual V5.0［Z］.2009

［2］Wold S，Esbensen K，Geladi P.Principal Component Analysis［J］.Chemometrics and Intelligent Laboratory Systems，1987，2（1）：37－52

［3］穆大鹏.基于主成分分析的GRACE 重力场模型等效水高［J］.地球物理学进展，2014，29（4）：1 512－1 517（Mu Dapeng.Equivalent Water Height from GRACE Gravity Model Based on Principal Component Analysis［J］.Progress in Geophysics，2014，29（4）：1 512－1 517）

［4］Johnson R A，Wichern D W.Applied Multivarariate Statistical Analysis［M］.Englewood Cliffs N J：Prentice Hall，1992

［5］Jolliffe I T.Principal Component Analysis［M］.New York：Springer，2012

［6］史文海，李正农，吴建佳.近地面强风不同间隔滑动平均统计特性的对比分析［J］.空气动力学学报，2013，31（5）：611－615（Shi Wenhai，Li Zhengnong，Wu Jianjia.A Contrastive Study of Different Time Interval Moving Average Statistical Characteristics of Strong Wind Near Ground［J］.Acta Aerodynamica Sinica，2013，31（5）：611－615）

［7］顾兆峰.KSS 31M 海洋重力仪静态观测结果及分析［J］.海洋测绘，2005，25（2）：66－68（Gu Zhaofeng.The Static Measurement Result of KSS 31M Marine Gravimeter and Its Analysis［J］.Hydrographic Surveying and Charting，2005，25（2）：66－68）