整体最小二乘和最小二乘拟合空间直线的比较
2015-02-15朱卫东钱承军
胡 川 陈 义,2 朱卫东 钱承军
1 同济大学测绘与地理信息学院,上海市四平路1239号,200092
2 现代工程测量国家测绘地理信息局重点实验室,上海市四平路1239号,200092
3 上海海洋大学海洋科学学院,上海市浦东新区南汇新城镇沪城环路999号,200120
三维空间直线拟合是工业测量中一个常见问题[1]。空间直线不能直接应用最小二乘法(least squares,LS)[2],而是采用点到直线距离平方和最小的拟合准则[3]进行拟合。该准则是一个非线性估计问题,文献[4]将其线性化后采用带约束条件的间接平差模型进行迭代求解。这种基于高斯迭代解的算法对初值非常敏感,可能出现不收敛情况。文献[3]用特征值分解法解决上述不收敛问题,并提出基于选权迭代的稳健空间直线拟合算法。因点到直线的距离不是直接观测值,该准则的最大困难是无法直接采用观测精度定权。
空间直线可用与坐标平面垂直的两个相交平面来表示。假设其中一个平面上的坐标观测值无误差,用LS法估计两个平面的参数,最后用两个拟合的平面恢复空间直线[5]。如果仅拟合其中一个平面,然后拟合空间直线在该平面上的投影线,即是文献[6]提出的无迭代算法。文献[7]将空间直线垂直投影到平面上,进行两两组合,选择其中点到直线距离和最小的组合作为空间直线参数的拟合结果。上述3 种方法都假设某些坐标无误差,这与实际不符。文献[2]提出采用整体最小二乘(total least squares,TLS)法拟合两个垂直投影平面,考虑了所有坐标误差,更符合实际,但没有考虑加权情况。
本文模拟各坐标点等精度、非等精度和各坐标分量非等精度的观测数据。将空间直线投影到坐标平面上,采用整体最小二乘法和最小二乘法对投影直线进行拟合。比较3 种模拟场景下TLS和LS估计的参数和验后方差,并比较三维激光扫描数据的拟合结果。
1 TLS拟合空间直线
1.1 拟合公式推导
假设一条空间直线通过点P0(x0,y0,z0),方向向量为(F,G,H),则直线的对称式方程为:

将上述空间直线投影到坐标平面上,有:

以XOY投影面上直线为例。设ey和ex分别是y和x的误差矢量,大小为m×1。它们的随机属性可以表达为[8,9]:

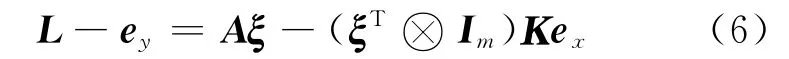
式中,L是由m个y分量组成的m×1矢量;A是m×2系数矩阵,其第一列由与y分量相对应的x分量组成,第二列全为常数1;ξ是待估计参数矢量;转换矩阵K计算公式为:
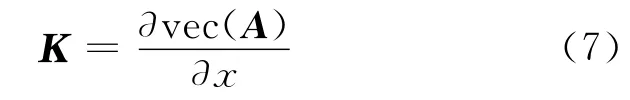
式(7)为矢量导数公式。引入TLS平差准则[8]:
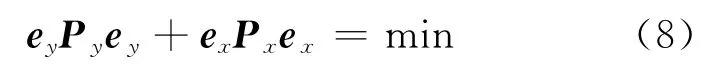
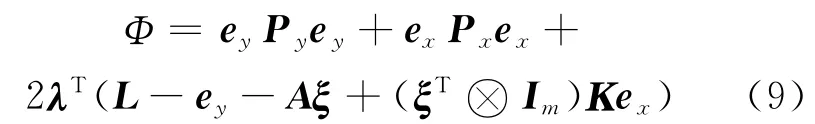
将式(9)分别对ey、ex、λ和ξ求偏导,并令其等于零,有[8]:

求解式(10)~(13),可以得到:
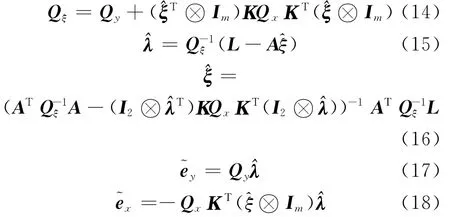
验后单位权方差为[8]:
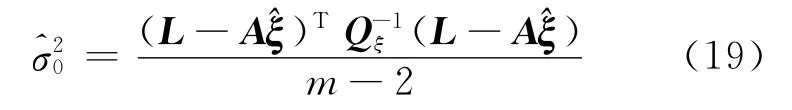
1.2 空间直线重建
根据拟合的平面直线,可以找到一个过该直线且垂直该坐标平面的平面,3个坐标平面得到3个垂直平面,平面两两组合可以重建出3条空间直线[7]。平面y-a1x-b1=0和z-a2y-b2=0的交线为:

平面z-a2y-b2=0和x-a3z-b3=0的交线为:

平面x-a3z-b3=0和y-a1x-b1=0的交线为:
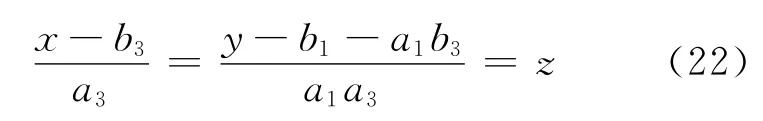
根据交叉出的3条空间直线的对称式,可以得到直线上的一个已知点和方向。可以采用下式计算点到直线的距离:
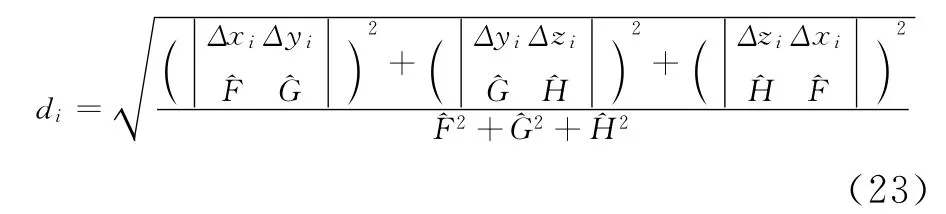
Δxi、Δyi和Δzi是测量点与对称方程中已知点的差值。
2 比较分析
2.1 模拟对比
设有已知空间直线:

在空间直线上任取10个精确坐标点。设置如下3种场景:
1)设所有测量点等精度观测,给各坐标点附加期望为零、方差分别为0.000 001、0.000 1、0.001、0.01、1.0m2的随机误差;
2)设所有测量点非等精度观测,按点的先后顺序附加上期望为零、方差从0.1m2增加到1m2的随机误差;
3)设所有测量点的坐标分量非等精度观测,给x、y、z坐标分量附加上期望为零、方差分别为0.8、0.4和0.2m2的随机误差。
在场景1中,协因数矩阵Qx、Qy和Qz都是单位阵,先验单位权方差分别为0.000 001、0.000 1、0.001、0.01、1.0 m2。在不同方差条件下,用LS和TLS各计算1 000次。参数估计值和验后单位权方差估计值的平均值列于表1。可以发现,在误差比较小时,LS和TLS估计的参数值几乎相同。当误差增大时,没有证据表明TLS获得的参数估计值比LS 更接近真实值。但是,多数情况下TLS的结果更接近真实值。不管在哪种方差条件下,TLS估计的验后单位权方差都比LS更接近先验值。
在场景2中,协因数矩阵Qx、Qy和Qz的对角线元素对应于各点模拟方差值,非对角线元素全为零,先验单位权方差为1。用LS和TLS分别计算10 000次。表2描述了场景2中LS和TLS计算的参数和验后单位权方差估计值。可以看出,不管是参数估计还是单位权方差估计结果,TLS明显要比LS更接近真实值,特别是方差估计值。
在场景3中,协因数矩阵Qx、Qy和Qz分别是0.8、0.4和0.2与单位矩阵的乘积,先验单位权方差为1m2,同样用LS和TLS分别模拟计算1 000次,将计算的平均值和平均值与真值的差值列于表3。可以发现,TLS 获得的参数估计值比LS更接近真实值。选择不同的坐标平面作为投影面,TLS 估计的参数与真值的差异非常小,但是LS对应不同的投影面,其估计结果与真值的接近程度不相同。换言之,TLS估计参数的准确性对投影面的依赖性比较小,而LS 依赖性较大。TLS获得的验后单位权方差比LS更接近真值。
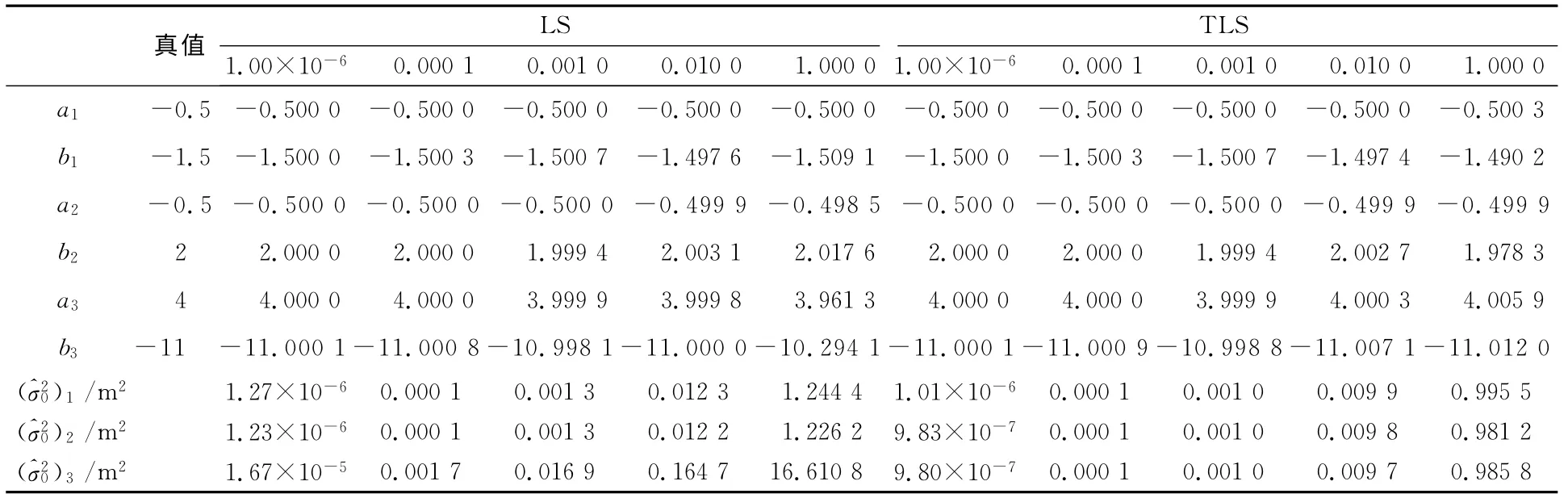
表1 场景1中LS和TLS计算的参数和验后单位权方差平均值Tab.1 Comparisons of the means of estimated parameters and variance of unit weight with LS and TLS in scenario 1

表2 场景2中LS和TLS计算的参数和验后单位权方差平均值以及与真值之差Tab.2 Comparisons of the mean of estimated parameters and variance of unit weight with LS and TLS,and the differences between the estimated value and real value in scenario 2
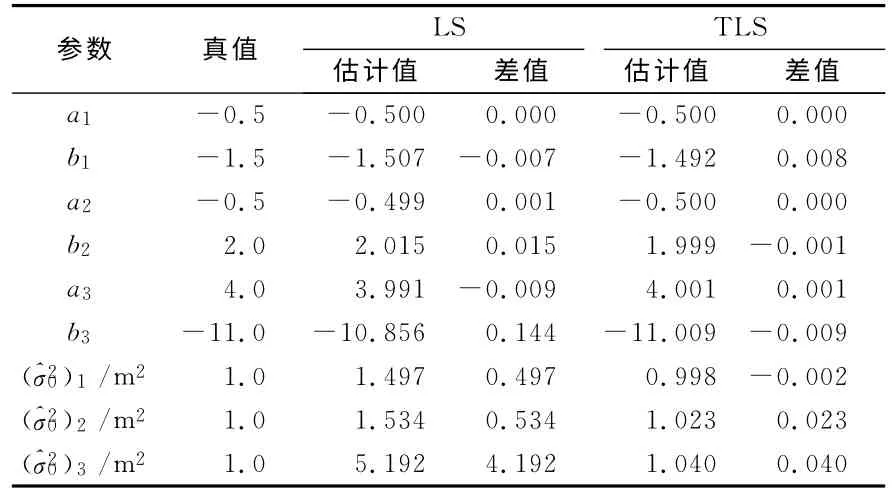
表3 场景3中LS和TLS计算的参数和验后单位权方差平均值以及与真值之差Tab.3 Comparisons of the mean of estimated parameters and variance of unit weight with LS and TLS,and the differences between the estimated value and real value in scenario 3
2.2 工程实践
用Faro三维激光扫描仪对新建的南京青奥步行桥进行三维激光扫描,提取六面体钢结构桥梁上两条边相交处的部分扫描点(图1)。菱形点是空间点在XOY面上的投影,五角星是空间点在XOZ面上的投影,小圆圈是空间点在YOZ面上的投影。

图1 扫描的三维坐标点Fig.1 Laser scanned data points
假设各点是等精度观测,权阵为单位矩阵,用LS法和TLS法分别拟合3条平面投影直线,将拟合的参数和验后单位权方差列于表4。可以看出,在XOY投影面的直线,两种方法拟合结果和验后方差完全相同。在其他两个投影面上,LS和TLS估计的参数和单位权方差出现较大差异,这与前面的模拟计算相符。但是,TLS估计的验后单位权方差也出现较大值,即明显较大。

表4 LS和TLS拟合扫描点的参数估计值Tab.4 Estimated parameters and variance of unit weight with LS and TLS using the laser scanned data points
将拟合的平面直线参数按照式(20)、(21)和(22)重建空间直线,分别称为空间直线(20)、(21)和(22)。采用式(23)分别计算各点到拟合空间直线的距离。图2描述了各点到LS和TLS拟合的空间直线(20)、(21)和(22)的距离。可以发现,扫描点到TLS拟合的空间直线的距离都非常接近,相反到LS拟合的空间直线的距离存在较大的差异。这说明,不管选择怎样的投影面,TLS法都可以得到近似相同的一条空间直线,而LS法不行。

图2 扫描点到拟合空间直线的距离Fig.2 The distance between the measured points and the fitted spatial lines
将各点到拟合空间直线距离之和的最大距离、最小距离和最大最小距离差列于表5。可以看出,TLS 重建的3 条直线的距离总和非常接近,而LS法重建的3 条直线距离总和存在较大差异,而且LS 的距离总和大于TLS 的距离总和。可以发现,TLS结果比LS 更加稳定。这与前面的结论相同,LS拟合结果对投影面的选择依赖性较强,而TLS的依赖性较弱。

表5 各点到空间直线的距离总和、最大值、最小值和最大小值之差/mTab.5 The sum of d,max d,min dand the differences between max and min,where dis the distance between the measured points and the fitted spatial lines/m
3 结 语
1)当已知各点坐标等精度观测的情况下,LS和TLS估计的空间直线参数几乎完全相同,但是TLS的验后方差分量估计值比LS的更接近先验值。此时,如果仅仅是为了估计参数,为了简便可以直接采用LS拟合空间直线;如果需要对参数估计结果进行统计评价,建议采用TLS拟合法。
2)当各点非等精度观测时,TLS估计的参数和验后单位权方差都比LS 的要更接近真实值。因此,此种情况建议使用TLS拟合法。
3)当各坐标分量非等精度观测时,LS拟合结果对投影面的选择具有较强的依赖性,而TLS的依赖性较弱。此时建议采用TLS进行空间直线拟合,选择任何两个投影面皆可。
4)对于三维激光扫描数据,TLS的拟合结果比LS更优。此时建议采用TLS法拟合,如果需要进一步提高拟合精度,需要合理确定各坐标分量的权值。
[1]陈基伟.工业测量数据拟合研究[D].上海:同济大学,2005(Chen Jiwei.Research on Industrial Measurement Data Fitting[D].Shanghai:Tongji University,2005)
[2]姚宜斌,黄书华,孔建,等.空间直线拟合的整体最小二乘算法[J].武汉大学学报:信息科学版,2014,39(5):571-574(Yao Yibin,Huang Shuhua,Kong Jian,et al.Total Least Squares Algorithm for Fitting Spatial Straight Line[J].Geomatics and Information Science of Wuhan University,2014,39(5):571-574)
[3]潘国荣,唐杭.特征分解与选权迭代在空间直线拟合中的应用[J].东南大学学报:自然科学版,2013,43(A2):250-255(Pan Guorong,Tang Hang.Application of Eigen Decomposition and Selecting Weight Iteration in Spatial Line Fitting[J].Journal of Southeast University:Natural Science Edition,2013,43(A2):250-255)
[4]王解先,季凯敏.工业测量拟合[M].北京:测绘出版社,2008(Wang Jiexian,Ji Kaimin.Industrial Measurement Fitting[M].Beijing:Surveying and Mapping Press,2008)
[5]袭杨.空间直线拟合的一种方法[J].齐齐哈尔大学学报:自然科学版,2009,25(2):64-68(Xi Yang.A Method for Fitting of a Space Straight Line[J].Journal of Qiqihar University:Natural Science Edition,2009,25(2):64-68)
[6]郭际明,向巍,尹洪斌.空间直线拟合的无迭代算法[J].测绘通报,2011(2):24-25(Guo Jiming,Xiang Wei,Yin Hongbin.Three-Dimensional Line Fitting without Iteration[J].Bulletin of Surveying and Mapping,2011(2):24-26)
[7]王伟锋,温耐.空间直线拟合研究[J].许昌学院学报,2010(5):37-39(Wang Weifeng,Wen Nai.Research on Fitting Method of Space Straight Line[J].Journal of Xuchang University,2010,9(5):37-39)
[8]Schaffrin B,Wieser A.On Weighted Total Least-Squares Adjustment for Linear Regression[J].Journal of Geodesy,2008.82(7):415-421
[9]胡川,陈义.解加权总体最小二乘平差问题的一种新方法[J].大地测量与地球动力学,2012,32(6):106-110(Hu Chuan,Chen Yi.An Innovation Algorithm for Solution of Weighted Total Least Squares Adjustment[J].Journal of Geodesy and Geodynamics,2012,32(6):106-110)
