基于全球MGEX数据的北斗导航星座精密轨道确定

李 冉 赵春梅 郑作亚 何正斌

1 山东科技大学测绘科学与工程学院，青岛市经济技术开发区前湾港路579号，266510

2 中国测绘科学研究院，北京市海淀区莲花池西路28号，100830

研究北斗卫星精密定轨对于发展北斗产业有重要意义［1－2］。国内外学者对北斗精密定轨作过大量研究。Montenbruck研究了北斗卫星区域导航系统的整体性能，得出轨道重叠弧段RMS 在1～10m［3］。刘伟平［4］利用BDS／GPS 双模观测数据进行BDS卫星精密定轨，得出MEO 与IGSO 卫星三维定轨精度优于0.5 m，GEO 卫星三维定轨精度优于5m。施闯［5］利用北斗卫星观测网数据和自主研发的PANDA 软件，开展北斗卫星导航系统精密定轨与定位的研究，得出重叠弧段径向精度优于0.1m。本文使用“两步法”以双差方式对北斗卫星进行精密定轨，并结合MGEX观测数据验证该方法的有效性和正确性。

1 北斗卫星精密定轨

1.1 利用广播星历形成初轨

本文采用广播星历作为初始轨道，利用GPS广播星历参数计算卫星轨道的方法适用于北斗MEO 和IGSO 卫星。由于北斗GEO 卫星的轨道倾角接近于0°，采用GPS广播星历参数形式拟合GEO 卫星轨道可能因矩阵奇异而不收敛，因此在计算GEO 卫星坐标时，算法有所不同［6］。

1）计算历元升交点赤径（惯性系下）：

2）计算GEO 卫星在自定义坐标系中的坐标：

3）计算GEO 卫星在CGCS2000坐标系中的坐标：

式中，

Ω0为按参考时间计算的升交点赤径,为升交点赤径变化率，tk为观测历元到参考历元的时间差，为地球旋转速率，toe为星历参考时间，（xk，yk）为计算得到的卫星在轨道平面内的坐标。

1.2 精密定轨方法及定轨模型

北斗轨道可采用两种方法确定：1）直接采用北斗观测数据进行北斗卫星精密定轨；2）利用相同测站的GPS数据进行精密单点定位，得出测站坐标和对流层参数之后，将所得参数作为已知值进行北斗卫星精密定轨，即所谓的“两步法”［7］。考虑到目前北斗导航系统全球组网尚未完成，地面观测站较少，并且第二种方法可以有效减少北斗卫星精密定轨中的待估参数，在一定程度上降低观测站几何位置分布不均的影响，因此本文采用第二种方法，以北斗卫星广播星历形成初轨，使用MGEX 观测数据固定测站坐标和对流层参数，利用双差模式对北斗卫星进行精密定轨。表1给出了轨道计算中涉及的测量模型和力学模型。

表1 北斗卫星定轨采用的测量模型和力学模型Tab.1 Measurement and mechanical models for Beidou satellite orbit determination

1.3 定轨处理流程

采用3d为一个定轨弧段，其主要定轨流程如图1所示。首先利用GPS精密星历及钟差和GPS观测数据进行精密单点定位，得出测站坐标和对流层参数。然后，将3d的北斗广播星历合并，计算其在J2000.0坐标下北斗卫星广播星历的位置序列。而后进行轨道积分，生成卫星初始轨道。同时将原始北斗观测数据组成单差观测方程，对数据进行预处理，形成双差观测方程。在此基础上，将测站坐标和对流层参数作为已知值加入力学模型，对轨道进行解算。对浮点解残差进行分析，删除异常的卫星和跟踪站。如果有跟踪站被删除，则需要重新生成基线进行解算，直到利用残差剔除异常值达到所设定的阈值则停止迭代，最终生成北斗卫星轨道3d解。

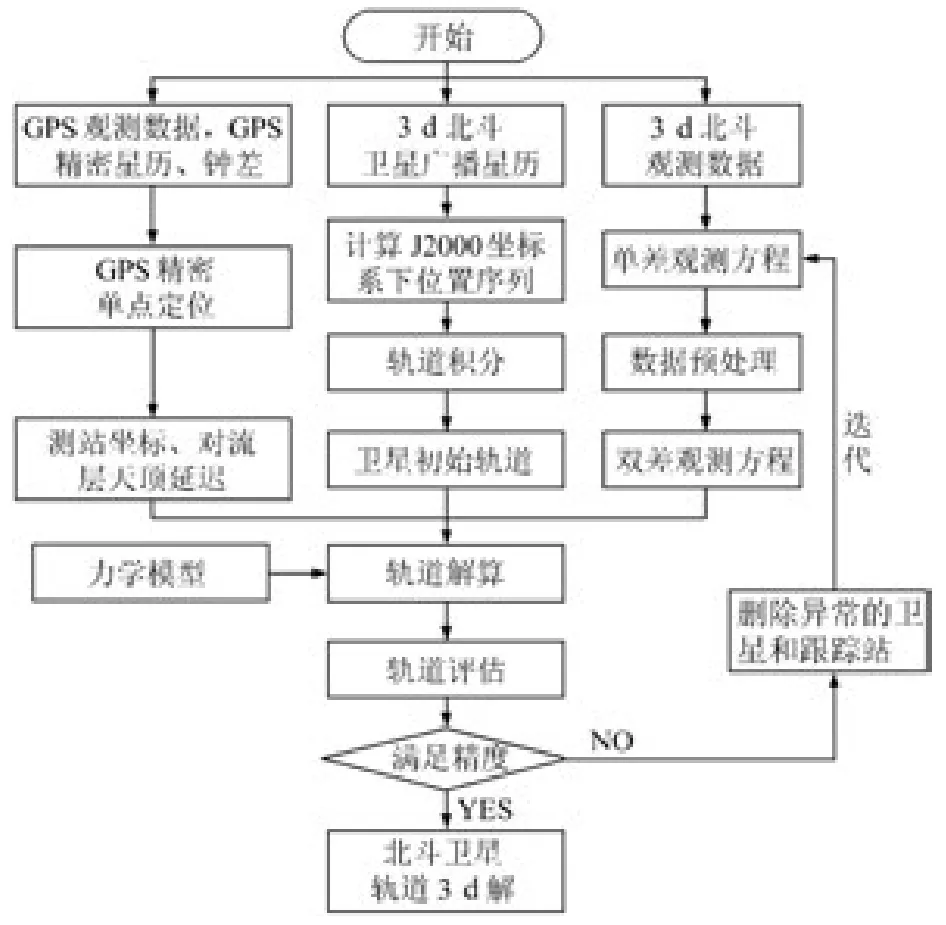
图1 轨道确定流程图Fig.1 Flow chart of orbit determination

2 实验分析

选取21个MGEX站2013－11－22～25（年积日第326～329d）共4d的观测数据，如图2所示。

图2 选取的MGEX 站分布图Fig.2 Distribution of select MGEX station

2.1 北斗IGSO 和MEO

2.1.1 内符合精度

由于北斗定轨是选取3d为一个定轨弧段，第一次得出2013年年积日为326～328d的定轨结果，第二次得出2013年年积日为327～329d的定轨结果，因此327d（11－23）和328d（11－24）为两次定轨的重叠弧段，可以通过比较重叠弧段的差异来评价定轨的内符合精度。图3为2013－11－23IGSO、MEO 的内符合精度。

图3 2013－11－23的IGSO、MEO 内符合精度Fig.3 The internal precision of IGSO／MEO

由图3可知，6～10号为IGSO 卫星，11～14号为MEO 卫星。图中给出了北斗IGSO、MEO沿迹方向（T）、径向（R）和法向（N）重叠弧段差异的RMS情况，卫星的径向定轨精度优于沿迹方向和法向，且径向精度都在10cm 以内，沿迹方向RMS在25cm 之内，法向在20cm 之内，1DRMS为16.33cm。

2.1.2 外符合精度

武汉大学发布了2013－11～12的北斗卫星精密星历（ftp：／／cddis.gsfc.nasa.gov／pub／gps／products／mgex／），通过与精密星历比较得出外符合精度。图4为2013－11－25IGSO、MEO 的外符合精度。与武汉大学精密星历比较，沿径向、迹向、法向轨道差异RMS 的均值为12.87cm，36.14cm，23.37cm，1D RMS 为25.94cm。可以看出，无论是内符合精度还是外符合精度，沿迹方向明显低于其他两个方向，这主要是由于沿迹方向的力未能通过力学模型完好地模拟，这也是动力学定轨的一般特性。

图4 2013－11－23的IGSO、MEO 外符合精度Fig.4 The outer precision of IGSO／MEO

之所以外符合精度较差，有以下原因：1）没有精确的北斗卫星天线PCO（相位中心偏差）、PCV（相位中心变化）信息，会对精密定轨精度产生影响；2）能够选择的观测站几何构型不佳，大部分能接收北斗数据的MGEX 站位于欧洲，而IGSO 卫星主要在亚太区域。

2.2 GEO 卫星定轨结果

由于C05号卫星在5个GEO 卫星中定点位置最偏西（58.75°E），而MGEX 站中能接收北斗信号的大多数位于欧洲，导致除C05号卫星外的其他4颗GEO 卫星接收数据太少，因此本文以C05号卫星为例，测试北斗GEO 卫星定轨情况，如图5。

从图5 可看出，GEO 卫星的定轨精度低于MEO 和IGSO，这是因为GEO 卫星与观测站之间的相对位置几乎保持不变，使卫星钟差与卫星轨道误差难以分离。正是由于这种静地性，增加了GEO 卫星定轨的难度。

可以看出，沿迹方向的定轨精度明显低于其他两个方向，除了沿迹方向的力未能通过力学模型完好地模拟外，还有可能是GEO 卫星沿迹方向存在系统差［4］。

图5 C05号卫星外符合精度Fig.5 The outer precision of C05satellite

3 结 语

1）通过本文方法，北斗MEO 和IGSO 卫星的1DRMS在20cm 之内，且径向都在10cm 内，外符合精度1D RMS优于30cm；对选取的5号GEO 卫星实验显示，外符合精度1D RMS 优于0.7m，径向优于10cm。总体上，IGSO、MEO 卫星定轨精度优于GEO 卫星，主要表现在GEO 卫星在沿迹方向的RMS偏大，这是因为GEO 卫星在动力学定轨中沿迹方向的力未能通过力学模型完好地模拟，且该方向存在着系统差。

2）对北斗卫星定轨采取“两步法”，首先利用MGEX 站接收的GPS 数据进行精密单点定位，产生对流层参数和测站坐标等公共参数，然后将公共参数作为已知值，利用双差方法对北斗卫星进行定轨，有效地减少了北斗卫星在精密定轨中的待估参数，在一定程度上降低了观测站分布不佳的不利影响。

3）能接收到北斗数据的MGEX 站大部分位于欧洲，而GEO 卫星主要位于亚太地区，能获得的GEO 卫星数据太少。因此，本文未能对所有GEO 卫星进行定轨分析。随着能够接收北斗卫星数据的MGEX 站（尤其是亚太地区）的增多，GEO 卫星定轨精度会有所提升。

［1］杨元喜.北斗卫星导航系统的进展、贡献与挑战［J］.测绘学报，2010，39（1）：1－6（Yang Yuanxi.Progress，Contribution and Challenges of Compass／Beidou Satellite Navigation System［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：1－6）

［2］冉承其.北斗卫星导航系统的发展［C］.第四届中国卫星导航学术年会，武汉，2013（Ran Chengqi.Development of Beidou Navigation Satellite System［C］.CSNC 2013，Wuhan，2013）

［3］Montenbruck O.Initial Assessment of the COMPASS／Beidou－2Regional Navigation Satellite System［J］.GPS Solutions，2013，17（2）：211－222

［4］刘伟平.一种北斗卫星精密定轨方法［J］.测绘科学技术学报2013，30（3）：248－250（Liu Weiping.A Method of Precise Orbit Determination of Beidou Navigation Satellite［J］.Journal of Geomatics Science and Technology.2013，30（3）：248－250）

［5］施闯，赵齐乐，李敏，等.北斗卫星导航系统的精密定轨与定位研究［J］.中国科学：地球科学，2012，42（6）：854－861（Shi Chuang，Zhao Qile，Li Min，et al.Precise Orbit Determination of Beidou Satellite with Precise Positioning［J］.Sci China Earth Sci 2012，42：854－861）

［6］中国卫星导航系统管理办公室.北斗卫星导航系统空间信息接口控制文件2.0［S］.北京，2013（China Satellite Navigation Office.Beidou Navigation Satellite System Signal in Space Interface Control Document V2.0［S］.Beijing，2013）

［7］李敏，赵齐乐，葛茂荣.GIOVE－A 卫星精密定轨仿真研究［J］.武汉大学学报：信息科学版，2008，33（8）：818－820（Li Min，Zhao Qile，Ge Maorong，GIOVE－A Satellite Precise Orbit Determination Simulation Research［J］.Geomatics and Information Science of Wuhan University，2008，33（8）：818－820）