BDS卫星天线相位中心改正模型比较

黄观文 张 睿 张 勤 郭海荣 王 乐

1 长安大学地质工程与测绘学院，西安市雁塔路126号，710054

2 地理信息工程国家重点实验室，西安市雁塔路中段1号，710054

3 北京卫星导航中心，北京市，100094

北斗系统的卫星天线相位中心改正主要有3种策略：第一种是国际多模GNSS 实验工程（MGEX）采用的方法，即只改正天线相位中心偏差（x＝0.6m，y＝0.0m，z＝1.1m），忽略PCV 改正。第二种是硬件制造商公布的策略［1］，也即改正天线相位中心偏差（x＝0.634 m，y＝－0.003m，z＝1.075 m），同样忽略PCV 改正值。第三种是欧空局ESA／ESOC 通过联合MGEX 网络北斗三频观测值解算得到的改正模型［2］，其针对北斗MEO 和IGSO 卫星均公布了新的PCV 和PCO 改正模型。国内外学者针对PCO 和PCV 模型开展研究［3－6］，但大多针对GPS系统，较少涉及BDS卫星天线相位中心模型的影响分析。本文针对这3种北斗卫星天线相位中心改正策略，从精密定轨、卫星钟差、精密定位3个方面分析不同改正策略的差异。

1 BDS卫星天线相位中心改正策略

IGS的北斗卫星天线相位中心改正策略简称MGEX 模型，即所有的GEO卫星、IGSO卫星以及MEO卫星都只进行天线相位中心偏差（PCO）改正，而不进行相位中心变化（PCV）改正，如表1。天线制造厂商建议的北斗卫星天线相位中心改正策略［1］简称厂商模型。该策略与MGEX模型类似，区别在于PCO 改正的数值略有差异，如表2所示。

表2 厂商模型的改正参数Tab.2 Corrections of Manufacturer model

欧空局ESA／ESOC通过收集MGEX 监测网络39个北斗地面跟踪站三频（B1，B2，B3）数据，利用B1－B2和B1－B3无电离层组合观测值进行解算，得到北斗IGSO和MEO卫星的PCO和PCV改正信息［2］。本文仅列出具体的PCO 和PCV 改正数值，如表3、4所示，简称ESA 模型。对于GEO 卫星，ESA／ESOC 还是采用了第一类MGEX改正策略，即只改正天线相位中心偏差（x＝0.6m，y＝0.0m，z＝1.1m），忽略PCV改正。

比较3种改正策略可以看出，MGEX 模型和厂商模型基本相同，仅在数值上存在3cm 左右的差异。而ESA 模型不仅区分出了不同卫星的PCO 改正值，其数值与前两种模型也存在较大不同。另外，ESA 模型还计算了IGSO 和MEO 卫星的PCV 改正数值。

表3 ESA／ESOC解算得到的BDS卫星天线相位中心偏差（PCO）改正Tab.3 PCO corrections of ESA／ESOC model of BDS

表4 ESA／ESOC解算得到的BDS卫星天线相位中心变化（PCV）改正Tab.4 PCV corrections of ESA／ESOC model of BDS

2 不同卫星天线相位中心改正策略的影响分析

2.1 不同改正策略对BDS精密定轨和精密钟差的影响

选取我国iGMAS 网络和国际MGEX 网络共65个BDS连续跟踪站观测数据，采集2014年第273～288d共15d的数据。对BDS卫星轨道和钟差进行解算，解算时使用的策略为3d解，共得到连续14个轨道和钟差的3d解。为对比不同卫星天线相位中心改正模型的精度差异，在评价轨道和钟差精度时采用重叠弧段方法进行［4］。设计4种天线改正方案进行求解：不进行任何改正（方案1）；MGEX 模型（方案2）；厂商模型（方案3）；ESA 模型（方案4）。

图1～4给出了4种方案得到的轨道重叠弧段在切向、法向、径向以及平均（1D）方向上的统计精度，图5～6给出了4种方案得到的卫星钟差重叠弧段的标准差精度（STD）和中误差精度（RMS）统计结果（C06号卫星为基准钟）。

对比图1～4及表5可以得出：

1）从4种方案的平均定轨结果（图4和表5）来看，方案4定轨精度最优，方案2、3相差不大，这与二者改正值较为接近有关。方案1不加任何改正的策略最差，平均精度显著差于其他方案。

图1 轨道重叠弧段切向精度Fig.1 Along precisions of orbit overlap error

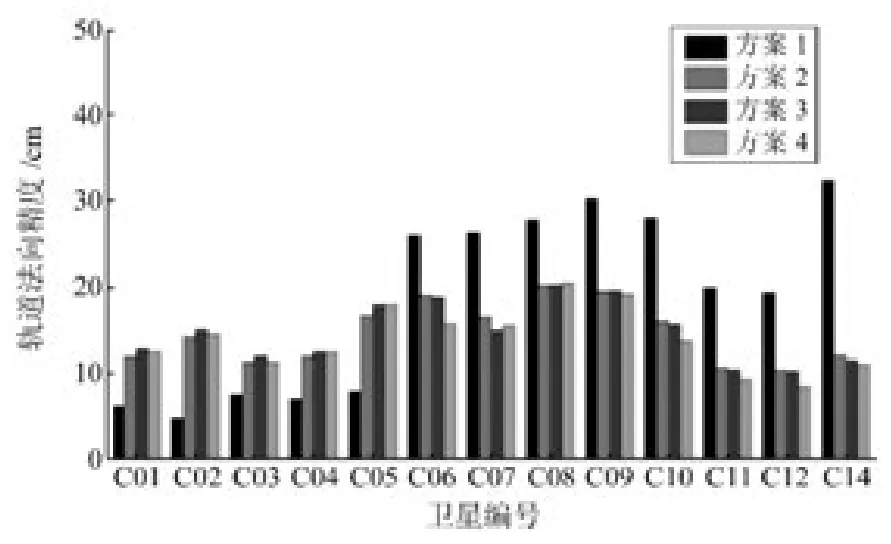
图2 轨道重叠弧段法向精度Fig.2 Cross precisions of orbit overlap error

图3 轨道重叠弧段径向精度Fig.3 Radial precisions of orbit overlap error

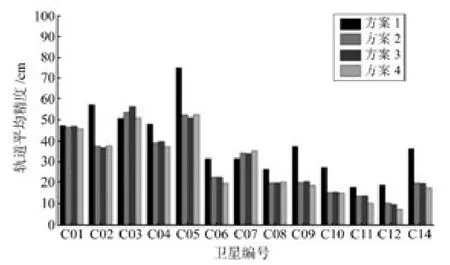
图4 轨道重叠弧段平均精度Fig.4 Average precisions of orbit overlap error

2）从4种方案3个方向的定轨精度对比（图2～4）来看，方案4最为稳定，方案2和方案3接近，方案1中GEO 卫星的法向精度要显著优于其他3 种方案，但由于其切向和径向精度较差，GEO 平均精度仍相对较差。

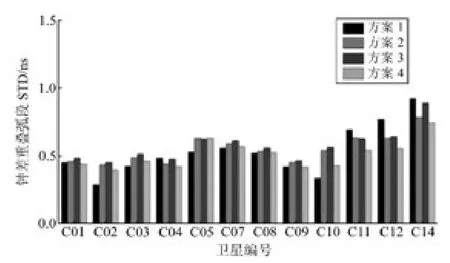
图5 卫星钟差重叠弧段STDFig.5 STD values of clock overlap error

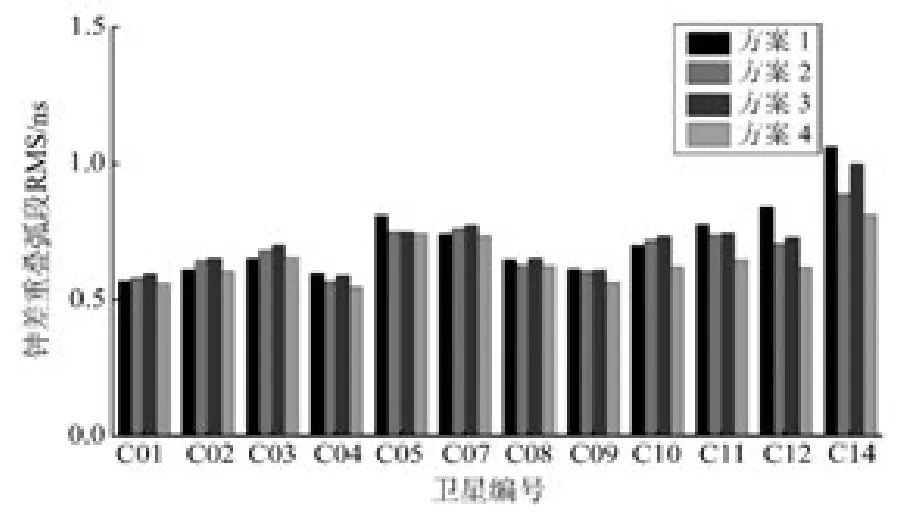
图6 卫星钟差重叠弧段RMSFig.6 RMS values of clock overlap error

3）方案4 的MEO 卫星定轨精度相对GEO和IGSO 卫星精度提升得更为显著，这与ESA 模型在MEO 方面的精细模型修正有关。

对比图5、6及表6中卫星钟差结果可以得出：

1）从4种方案的平均钟差结果（表6）来看，方案4的STD 和RMS均显著优于方案2和方案3，尤其是MEO 卫星钟差精度提升最为明显。

2）方案1钟差STD 指标除MEO 卫星稍差外，GEO和IGSO结果都与其他3种方案近似（表6）。方案1 钟差结果RMS除MEO 卫星稍差外，GEO 和IGSO 结果都与方案2和方案3近似，略差于方案4（表6）。这表明，天线相位中心改正对卫星钟差产品精度的影响要显著小于轨道产品精度影响。

3）从图5、6看出，方案4相对其他方案最为稳定，卫星钟差精度也最高。这也说明，通过精确的卫星天线相位中心改正，可以在一定程度上提升卫星钟差产品的精度。

2.2 BDS精密单点定位精度分析

为进一步分析不同天线改正策略对用户定位精度的影响，选取§2.1相同时段内武汉大学北斗跟踪站网络（BETS）5个连续跟踪站15d的观测数据进行处理，基于4种策略得到的卫星轨道和钟差，采用上述4种天线改正模型各自进行静态精密单点定位解算。计算时使用单天解策略，统计每个跟踪站的点位重复精度即STD指标。同时，为了对比测站结果的外符合精度，利用测站上GPS观测数据进行15d的精密单点定位计算，获得平均测站坐标值作为真值（精度优于1cm），计算不同方案所获测站坐标的外符合精度值（RMS）。

1）从表7中4种方案的点位重复精度（STD）可以看出，方案4的点位重复精度最高，方案2和方案3相当，方案1最差。但从数值上看，4种方案的STD 指标差异均在mm 量级，这说明采用不同方案自洽的轨道钟差产品进行单独定位，所获定位结果内符合精度均近似等价。

2）从表8 中4 种方案的外符合精度（RMS）可以看出，方案4的定位精度最高，方案2和方案3相当，方案1最差。且从数值上看，方案4的定位精度显著优于其他3种方案。对比表7的方案4结果可以得出，虽然不同方案自洽的轨道钟差产品进行单独定位，所获内符合精度差异较小，但更准确的天线改正模型可以显著提高用户定位的外符合精度。

3 结 语

1）ESA 模型的精密定轨精度和稳定性要优于MGEX 模型和厂商模型，尤以MEO 卫星定轨精度改善最为显著。MGEX 模型和厂商模型的定轨精度相差不大，这与二者改正值较为接近有关，而不加任何天线改正的定轨结果要显著差于其他模型。

表5 4种方案得到的不同星座轨道重叠精度统计结果Tab.5 Precisions of orbit overlap error from different schemes

表6 4种方案得到的不同星座钟差重叠精度统计结果Tab.6 Precisions of clock offset overlap error from different schemes

2）不同的天线相位中心改正模型对于卫星钟差产品的精度影响要显著小于轨道产品，更为精确的卫星天线相位中心模型（ESA 模型）可以在一定程度上提升卫星钟差产品的精度。

3）利用不同天线模型自洽的轨道钟差产品进行单独精密定位，所获结果的内符合精度差异较小，但更准确的天线改正模型可以显著提高用户定位的外符合精度。

表7 4种方案得到的点位重复精度STD统计结果Tab.7 Repeated accuracy of point coordinates from different schemes

表8 4种方案得到的坐标RMS统计结果Tab.8 RMS results of stations coordinates from different schemes

致谢：感谢iGMAS和IGS以及武汉大学提供的数据支持。

［1］Lou Y，Liu Y，Shi C，et al.Precise Orbit Determination of Beidou Constellation Based on BETS and MGEX Network［J］.Sci Rep，2014，4（8）：1 255－1 264

［2］Dilssner F，Springer T，Schönemann E，et al.Estimation of Satellite Antenna Phase Center Corrections for Beidou［C］.IGS Network，Data and Analysis Center Workshop，Pasadena，California，2014

［3］胡志刚.北斗卫星导航系统性能评估理论与试验验证［D］.武汉：武汉大学，2013（Hu Zhigang.Beidou Navigation Satellite System Performance Assessment Theory and Experimental Verification［D］.Wuhan：Wuhan University，2013）

［4］张小红，李盼，李星星，等.天线相位中心改正模型对PPP参数估计的影响［J］.武汉大学学报：信息科学版，2011，12（36）：1 470－1 473（Zhang Xiaohong，Li Pan，Li Xingxing，et al.Influcence of Antenna Phase Center Correction Model on Precise Point Positioning［J］.Geomatics and Information Science of Wuhan University，2011，12（36）：1 470－1 473）

［5］涂锐，黄观文，邹顺.天线相位中心偏差变化及改正模型对精密单点定位精度的影响［J］.大地测量与地球动力学，2010，30（3）：113－117（Tu Rui，Huang Guanwen，Zhou Shun.Study on Impact of Antenna Phase Center Offsets Variation and Their Correction Models on GPS Precise Point Positioning Accuracy［J］.Journal of Geodesy and Geodynamice，2010，30（3）：113－117）

［6］丁晓光，张勤，黄观文，等.GPS天线相位模型变化对高精度GPS测量解算的影响研究［J］.测绘科学，2010，35（3）：18－20（Ding Xiaoguang，Zhang Qin，Huang Guanwen，et al.Influence of GPS Antenna Phase Center Model Change on GPS Data Processing［J］.Science of Surveying and Mapping，2010，35（3）：18－20）